| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
MarinaMarina
Gost
|
 Postano: 13:54 sub, 1. 6. 2013 Naslov: Postano: 13:54 sub, 1. 6. 2013 Naslov: |
    |
|
|
Ispricavam se ako negdje pise, ali ja nigdje ne mogu naci rezultate od proslogodisnjeg drugog kolokvija, a voljela bi si provjeriti rjesenja, pa ako netko ima rjesenja, molila bi da mi ih napise, hvala!
Ispricavam se ako negdje pise, ali ja nigdje ne mogu naci rezultate od proslogodisnjeg drugog kolokvija, a voljela bi si provjeriti rjesenja, pa ako netko ima rjesenja, molila bi da mi ih napise, hvala!
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
 Postano: 19:22 sub, 1. 6. 2013 Naslov: Postano: 19:22 sub, 1. 6. 2013 Naslov: |
    |
|
|
Opet ja, nadam se zadnji puta. Prema [b]Teoremu 7.12[/b], postoji lijepa rekurzija za rješenja jednadžbe [tex]x^2-dy^2=1[/tex] u prirodnim brojevima. Ali postoji li nešto slično ako je na desnoj strani [tex]-1[/tex]? U [b]Primjeru 7.3[/b] imamo sreće što je period u razvoju paran pa ta jednadžba nema rješenja, ali što ako problem bude formuliran kao u tom primjeru i rješenja za taj slučaj budu postojala? Čini mi se da je onda jedini način tablično kao u idućem primjeru, ali opet, ta bi se tablica mogla "rastegnuti" ako bude bio npr. "velik" period ili "veliko" gornje ograničenje. Imamo li olakotnih postupaka u tom slučaju?
Opet ja, nadam se zadnji puta. Prema Teoremu 7.12, postoji lijepa rekurzija za rješenja jednadžbe [tex]x^2-dy^2=1[/tex] u prirodnim brojevima. Ali postoji li nešto slično ako je na desnoj strani [tex]-1[/tex]? U Primjeru 7.3 imamo sreće što je period u razvoju paran pa ta jednadžba nema rješenja, ali što ako problem bude formuliran kao u tom primjeru i rješenja za taj slučaj budu postojala? Čini mi se da je onda jedini način tablično kao u idućem primjeru, ali opet, ta bi se tablica mogla "rastegnuti" ako bude bio npr. "velik" period ili "veliko" gornje ograničenje. Imamo li olakotnih postupaka u tom slučaju?
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
mata
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (17:50:57)
Postovi: (17)16
|
 Postano: 20:11 sub, 1. 6. 2013 Naslov: Postano: 20:11 sub, 1. 6. 2013 Naslov: |
    |
|
|
http://web.math.pmf.unizg.hr/~duje/utb/kol12_2.pdf
Molim pomoc! Zanima me kako se rjesava 4. zadatak, tj kako da zapisem broj [1,1,2,3,1,2] gdje se 2,3,1,2 ponavlja u obliku racionaliziranog skracenog razlomka?
http://web.math.pmf.unizg.hr/~duje/utb/kol12_2.pdf
Molim pomoc! Zanima me kako se rjesava 4. zadatak, tj kako da zapisem broj [1,1,2,3,1,2] gdje se 2,3,1,2 ponavlja u obliku racionaliziranog skracenog razlomka?
|
|
| [Vrh] |
|
kiara
Forumaš(ica)

Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
 Postano: 14:03 ned, 2. 6. 2013 Naslov: Postano: 14:03 ned, 2. 6. 2013 Naslov: |
    |
|
|
[quote="mata"]http://web.math.pmf.unizg.hr/~duje/utb/kol12_2.pdf
Molim pomoc! Zanima me kako se rjesava 4. zadatak, tj kako da zapisem broj [1,1,2,3,1,2] gdje se 2,3,1,2 ponavlja u obliku racionaliziranog skracenog razlomka?[/quote]
pogledaj si u skripti na 69.str, primjer 6.5
kao beta stavis ovo sto se ponavlja,znaci beta=[2,3,1,2],kada rjesis tu jednadzbu,dobit ces beta i to uvrstis u alfa koje je=[1,1,2,3,1,2] tj. [1,1,beta] i iz toga dobis alfu u obliku racionaliziranog skracenog razlomka
| mata (napisa): | http://web.math.pmf.unizg.hr/~duje/utb/kol12_2.pdf
Molim pomoc! Zanima me kako se rjesava 4. zadatak, tj kako da zapisem broj [1,1,2,3,1,2] gdje se 2,3,1,2 ponavlja u obliku racionaliziranog skracenog razlomka? |
pogledaj si u skripti na 69.str, primjer 6.5
kao beta stavis ovo sto se ponavlja,znaci beta=[2,3,1,2],kada rjesis tu jednadzbu,dobit ces beta i to uvrstis u alfa koje je=[1,1,2,3,1,2] tj. [1,1,beta] i iz toga dobis alfu u obliku racionaliziranog skracenog razlomka
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
 Postano: 20:01 ned, 2. 6. 2013 Naslov: Postano: 20:01 ned, 2. 6. 2013 Naslov: |
    |
|
|
[quote="Anonymous"]Trebala bi pomoć s Pellovim jednadžbama, u skripti je u primjeru 7.4. riješen zadatak pomoću tablice. Moće li mi netko reći kako se računaju p(n) i q(n). Hvala.[/quote]
[latex]p_{-1}, p_0 [/latex] su fiskni [latex]( p_0 = a_0 ), q_0 , q_1 [/latex] su također fiskni.
dalje računaš :
[latex]p_{n+1} = a_{n+1} * p_n + p_{n-1} [/latex] ( dakle, za ovu tablicu je [latex]p_1 = 5*2 + 1 = 11 [/latex] )
dakle, množiš s elementom gore desno, plus jedan lijevo.
tako radiš i za [latex]q_n[/latex].
dakle, euklidov algoritam u biti pomoću one tablice isto.
( kao u primjeru 1.2. )
| Anonymous (napisa): | | Trebala bi pomoć s Pellovim jednadžbama, u skripti je u primjeru 7.4. riješen zadatak pomoću tablice. Moće li mi netko reći kako se računaju p(n) i q(n). Hvala. |
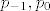 su fiskni su fiskni 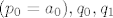 su također fiskni. su također fiskni.
dalje računaš :
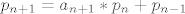 ( dakle, za ovu tablicu je ( dakle, za ovu tablicu je 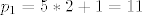 ) )
dakle, množiš s elementom gore desno, plus jedan lijevo.
tako radiš i za 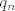 . .
dakle, euklidov algoritam u biti pomoću one tablice isto.
( kao u primjeru 1.2. )
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 21:30 pon, 3. 6. 2013 Naslov: Postano: 21:30 pon, 3. 6. 2013 Naslov: |
    |
|
|
ne mogu "provalit" kako se iz tablice izvlače rješenja, recimo za primjer 7.4 iz skripte.
Slutim da ima veze sa iskazom teorema 7.10, njegovim drugim dijelom, naime x se izjednačava sa brojnikom neke konvergente p_nr-1 ali koji se to n množi sa duljinom periode smanjene za jedan?
Citat iz skripte:
"To znaci da je period r = 5 neparan, pa je najmanje rjesenje od x^2 - 29y^2 = -1 dano sa (p4, q4), a najmanje rje·senje sa (p9, q9)."
Dakle koliko shvaćam, po iskazu iz gornjeg teorema, p-ov indeks(i q-ov) je dobiven produktom jedinice sa duljinom periode smanjene za jedan ali otkud n=1? Isto pitanje za p_9 .
ne mogu "provalit" kako se iz tablice izvlače rješenja, recimo za primjer 7.4 iz skripte.
Slutim da ima veze sa iskazom teorema 7.10, njegovim drugim dijelom, naime x se izjednačava sa brojnikom neke konvergente p_nr-1 ali koji se to n množi sa duljinom periode smanjene za jedan?
Citat iz skripte:
"To znaci da je period r = 5 neparan, pa je najmanje rjesenje od x^2 - 29y^2 = -1 dano sa (p4, q4), a najmanje rje·senje sa (p9, q9)."
Dakle koliko shvaćam, po iskazu iz gornjeg teorema, p-ov indeks(i q-ov) je dobiven produktom jedinice sa duljinom periode smanjene za jedan ali otkud n=1? Isto pitanje za p_9 .
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
|






