Kombinatorika

[mimar]

Pozdrav! Da li mozete reci kako se rijesavaju zadaci:

1. Odredite konstantan clan u (2x- 1/x)^6?

2. Odredite koeficijent uz x^5 u (1+x+x^2)^52?

Hvala!

[Phoenix]

Po multinomnom teoremu vrijedi formula
[tex](x_1+x_2+...+x_k)^n= \sum \limits_{n_1+n_2+...+n_k=n}{n \choose n_1,n_2,...,n_k}x_1^{n_1}x_2^{n_2}...x_k^{n_k}[/tex]
Ova formula će nam trebati za oba zadatka.

1. Ako je [tex]n=6[/tex], [tex]k=2[/tex], [tex]x_1=2x[/tex] i [tex]x_2=-\frac{1}{x}[/tex], dobivamo:
[tex](2x-\frac{1}{x})^6 = \sum \limits_{n_1+n_2=6}{6 \choose n_1,n_2}(2x)^{n_1}\left( -\frac{1}{x} \right)^{n_2} = \sum \limits_{n_1+n_2=6}\frac{6!}{n_1! n_2!}(2x)^{n_1}\left( -\frac{1}{x} \right)^{n_2}= \sum \limits_{n_1+n_2=6}\frac{6!}{n_1! n_2!}2^{n_1}(-1)^{n_2}x^{n_1-n_2}[/tex]
Prva jednadžba koja mora vrijediti jest [tex]n_1+n_2=6[/tex]. Kako tražiš koeficijent uz konstantni član, sumiraš vrijednosti po takvim [tex]n_1[/tex] i [tex]n_2[/tex] da vrijedi [tex]n_1-n_2=0[/tex] (odnosno, jednaki su).
Rješenje sustava ovih dviju jednadžbi je jedinstveno: [tex]n_1=n_2=3[/tex], pa dobivaš da je traženi konstantni član jednak:
[tex]\frac{6!}{3!3!}2^3 (-1)^3 = -160[/tex].

2. Slično naštimaš [tex]n=52[/tex], [tex]k=3[/tex], [tex]x_1=1[/tex], [tex]x_2=x[/tex], [tex]x_3=x^2[/tex], pa dobivaš:
[tex](1+x+x^2)^{52}= \sum \limits_{n_1+n_2+n_3=52}{52 \choose n_1,n_2,n_3}1^{n_1}x^{n_2}(x^2)^{n_3}= \sum \limits_{n_1+n_2+n_3=52}{52 \choose n_1,n_2,n_3} x^{n_2+2n_3}[/tex]
Sada imaš sljedeće jednadžbe:
[tex]n_1+n_2+n_3=52[/tex]
[tex]n_2+2n_3=5[/tex]
Rješenje ovog sustava nije jedinstveno pa ćeš imati više sumanada s potencijom [tex]5[/tex]. Srećom, zbog druge jednadžbe imaš uvjet [tex]2n_3 \leq 5[/tex], odnosno [tex]n_3 \leq 2[/tex]. Stoga i nemaš toliko puno slučajeva kako se na početku činilo: [tex]n_3[/tex] je jednak [tex]0, 1[/tex] ili [tex]2[/tex], a ako znaš koliko je [tex]n_3[/tex], znaš koliko je i [tex]n_2[/tex] (iz druge jednadžbe), pa i [tex]n_1[/tex] (iz prve jednadžbe) - dakle, imaš ukupno tri mogućnosti.
Suma je bila oblika (multinomni koeficijent)*([tex]x[/tex] na nešto), stoga je tvoje rješenje suma tri multinomna koeficijenta.
(Koliko treba raspisati i izračunati te multinomne koeficijente do kraja, iskreno, ne znam. U ovom zadatku se pojavljuju malo veći brojevi u rješenju pa se isplati pitati na kolokviju bude li i ove godine sličan slučaj. )

[JV]

Napomena za kolokvij iz kombinatorike:
Na kolokviju nisu dopuštene formule, samo pribor za pisanje (brisanje).

[rimidalv1991]

A kalkulator?

[Gost]

Hoće li biti teorije (predavanja) u kolokviju? Mislim, to mi nema smisla ako moramo ić na usmeni :S

[Megy Poe]

[umpa_lumpa]

Da li može netko napisati koliko mu je ispalo rješenje u 6.zad iz kolokvija od prošle godine?

[Gost]

Jel zna itko 7. zadatak od prošle godine?

[Gost]

A u 6. zadatku je rješenje 15...

[Gost]

Rj. u 6. je 16, a ne 15...

[Gost]

Je je, 16 ne 15, tipfeler.. A kad si tako pametan/na jel imas 7.? Hihihihi

[Gost]

Neka su oznake vrhova P1,...P_(2n). Postoji neki s neparnim indeksom koji spajas s nekim s parnim indeksom, BSO P1 spajam sa P_(2k). Ta duzina razdvaja mnogokut u 2 disjunktna dijela od kojih svaki ima paran broj vrhova (jedan ima 2(k-1), a drugi 2(n-k)), pa na svakom od tih mnogokuta mogu napraviti konfiguraciju od (k-1) i (n-k) duzina, tj. ukupno 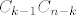. Posto je k proizvoljan, prosumiras od 1 do n i gotovo.

[umpa_lumpa]

A polinom se dobije 7x^3 + 16x^2 + 8x + 1?

[Gost]

A kako bi rješili 5.zadatak pod b, prošlogodišnji kolokvij? http://web.math.pmf.unizg.hr/nastava/kombd/kolokvij1.pdf
Hvala

[Gost]

Ovo pod b racunas bas po toj rekurziji, imas neki teorem da ti je to jednako, samo u principu je teorem da je broj polja u prvom retku jednak k, pa ti je to isto ako transponiras dijagram, racunas dakle k=4 i n=11, rekurziju isfuras ono do k=2 pa na prste ili mozes i do k=1

[Gost]

Može li mi netko reći što je ovo danas bilo? Jel samo meni bio težak kolokvij, da ne kažem nerješiv u 2 sata, ili ćemo nešto poduzeti po pitanju ovoga? I zna li itko kad će rezultati? I postoji li koji genijalac koji je rješio sve ovo da meni, očito idiotu, kaže rješenja?

[Gost]

Meni je ovo isto bilo strašno, užas!

[Gost]

Znaci nisam jedini 'idiot' koji ovo nije znao riješiti? I što sada dalje? Pretpostavljam da asistenti nemaju komentara... Jel se mi imamo kome žaliti na ovo? Jer mislim da nije u redu, ako smo došli do ovdje, znači da smo položili i puno teže kolegije. Neda mi se biti neki pokusni kunić na kojima će se iskušavati koliko težak ovaj predmet može biti i koliko još gradiva trebaju uvrstiti u vježbe koje su KATASTROFALNO odrađene!

[Gost]

A ne znam kome bi se mogli zaliti, ali u svakom slucaju treba kolektivno asistentima na vjezbama reci da ovo uopce nije imalo smisla... ili skupit 15-20 ljudi koji ce na predavanju jednoglasno to reci profesoru.
Cuo sam i da je asist.Vujcic namjeravao umjesto 6. staviti zadatak tezine kao 5. i 7. - sto bi tek onda bilo .
Po meni, netko tko bi inace dobio 25 bodova na kolokviju, ove godine ce dobiti 10

[Gost]

Naravno, pa ja sam prvi takav primjer. Svake druge godine bi kolokvij bio rješen za 5, a ove godine ne znam da li ću uspjeti skupiti 10 bodova.

Ma jel to onaj isti dragi asistent Vujčić koji bi se pogubio svaki put kad bi ga nešto pitali i promjenio tisuću boja jer nam ne zna odgovoriti pa bi svaki odgovor izgledao otprilike ovako: 'Ali Matija je ovdje tako napisao!'

Poštovani asistente Vujčiću, ukoliko ćete nam zadavati ovako bolesne zadatke, molimo da se onda bolje pripremite za vježbe i bolje nam to ispredajete. Znamo da ste novi, ali to ne znači da mi moramo ispaštati. Hvala Vam što ste od ovoga predmeta, koji je bio zabavan, napravili teški idiotizam i nadam se da ste zadovoljni prosječnim brojem bodova koji neće prelaziti 15. Ja znam da sigurno jedna osoba neće biti zadovoljna s tim: profesor Svrtan kada vidi što mu radite od predmeta.

A ja ću prvi istupiti na predavanjima i reći profesoru kako stoje stvari jer ovo nije nimalo u redu.