| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
malisputnik
Forumaš(ica)
Pridružen/a: 02. 09. 2013. (08:43:21)
Postovi: (31)16
|
|
| [Vrh] |
|
rom
Forumaš(ica)
Pridružen/a: 26. 10. 2010. (11:10:35)
Postovi: (2D)16
|
|
| [Vrh] |
|
malisputnik
Forumaš(ica)
Pridružen/a: 02. 09. 2013. (08:43:21)
Postovi: (31)16
|
|
| [Vrh] |
|
angelika
Forumaš(ica)

Pridružen/a: 08. 02. 2011. (17:26:51)
Postovi: (5F)16
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
 Postano: 12:54 čet, 6. 2. 2014 Naslov: Postano: 12:54 čet, 6. 2. 2014 Naslov: |
    |
|
|
[quote="angelika"]Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć[/quote]
Je li ovo dobra slicnost:
f:QU<0,1> -> QU<0,korijen iz 2]
f(x) = x, x<=0 i x>1
f(x) = (korijen iz 2)*x, 0<x<=1
| angelika (napisa): | Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć |
Je li ovo dobra slicnost:
f:QU<0,1> → QU<0,korijen iz 2]
f(x) = x, x⇐0 i x>1
f(x) = (korijen iz 2)*x, 0<x⇐1
_________________
Lakše je naučiti matematiku nego raditi bez nje.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 13:06 čet, 6. 2. 2014 Naslov: Postano: 13:06 čet, 6. 2. 2014 Naslov: |
    |
|
|
[quote="slonic~tonic"][quote="angelika"]Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć[/quote]
Je li ovo dobra slicnost:
f:QU<0,1> -> QU<0,korijen iz 2]
f(x) = x, x<=0 i x>1
f(x) = (korijen iz 2)*x, 0<x<=1[/quote]
Ovako definirana funkcija niti je injektivna ([tex]f\left(\frac{11\sqrt{2}}{20}\right)=\frac{11}{10} = f\left(\frac{11}{10}\right)[/tex]), niti čuva uređaj ([tex]f(1) = \sqrt{2}[/tex], a [tex]f\left(\frac{11}{10}\right) = \frac{11}{10}[/tex]). Prema tome, to nije sličnost.
| slonic~tonic (napisa): | | angelika (napisa): | Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć |
Je li ovo dobra slicnost:
f:QU<0,1> → QU<0,korijen iz 2]
f(x) = x, x⇐0 i x>1
f(x) = (korijen iz 2)*x, 0<x⇐1 |
Ovako definirana funkcija niti je injektivna ([tex]f\left(\frac{11\sqrt{2}}{20}\right)=\frac{11}{10} = f\left(\frac{11}{10}\right)[/tex]), niti čuva uređaj ([tex]f(1) = \sqrt{2}[/tex], a [tex]f\left(\frac{11}{10}\right) = \frac{11}{10}[/tex]). Prema tome, to nije sličnost.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
aptx
Forumaš(ica)

Pridružen/a: 11. 01. 2013. (00:15:01)
Postovi: (15)16
|
|
| [Vrh] |
|
malisputnik
Forumaš(ica)
Pridružen/a: 02. 09. 2013. (08:43:21)
Postovi: (31)16
|
 Postano: 13:31 čet, 6. 2. 2014 Naslov: Postano: 13:31 čet, 6. 2. 2014 Naslov: |
    |
|
|
[quote="aptx"][quote="angelika"]Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć[/quote]
Meni se čini da nisu slični (topološka potpunost?)[/quote]
Svaki podskup ovih skupova ima supremum u danom skupu. Za Q je ocito, trebamo pogledati za 'drugi dio skupa'.
Skup <0,1> ima superemum 1 sto je element iz Q pa je supremum u skupu Q unija <0,1>.
U drugom skupu <0, korijen(2)] ima supremum u korijen(2) sto je opet u Q unija <1, korijen(2)].
| aptx (napisa): | | angelika (napisa): | Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć |
Meni se čini da nisu slični (topološka potpunost?) |
Svaki podskup ovih skupova ima supremum u danom skupu. Za Q je ocito, trebamo pogledati za 'drugi dio skupa'.
Skup <0,1> ima superemum 1 sto je element iz Q pa je supremum u skupu Q unija <0,1>.
U drugom skupu <0, korijen(2)] ima supremum u korijen(2) sto je opet u Q unija <1, korijen(2)].
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 13:45 čet, 6. 2. 2014 Naslov: Postano: 13:45 čet, 6. 2. 2014 Naslov: |
    |
|
|
[quote="malisputnik"][quote="aptx"][quote="angelika"]Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć[/quote]
Meni se čini da nisu slični (topološka potpunost?)[/quote]
Svaki podskup ovih skupova ima supremum u danom skupu.
[/quote]
Ovo nije istina, jer [tex]\mathbb{Q}[/tex] [b]nije[/b] potpun.
I da skratimo priču, [url=http://degiorgi.math.hr/forum/viewtopic.php?p=186121#186121]ponavljam[/url], slični su i relativno se lagano pokaže postojanje sličnosti.
| malisputnik (napisa): | | aptx (napisa): | | angelika (napisa): | Jesu li Q unija <0,1> i Q unija <0, korjen iz 2] slični?
Čini mi se da jesu ali ne mogu naći sličnost...može pomoć |
Meni se čini da nisu slični (topološka potpunost?) |
Svaki podskup ovih skupova ima supremum u danom skupu.
|
Ovo nije istina, jer [tex]\mathbb{Q}[/tex] nije potpun.
I da skratimo priču, ponavljam, slični su i relativno se lagano pokaže postojanje sličnosti.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
nuclear
Forumaš(ica)


Pridružen/a: 13. 11. 2011. (17:40:12)
Postovi: (74)16
Spol: 
|
 Postano: 13:58 čet, 6. 2. 2014 Naslov: Postano: 13:58 čet, 6. 2. 2014 Naslov: |
    |
|
|
Ako mi netko može ovo objasniti jer ne vidim odgovor :D
Na vježbama smo napisali da je {0,1}x Z lokalno konačan skup i da je
k([(a,b),(c,d)])<=(d-b+1)*2
Sad meni nije jasno, nije li k( [(0,0),(1,0)])= aleph 0?
jer se "putuje" po drugoj varijabli (0,x) od (0,0) do (1,0) i kao tek u beskonačnosti postane (0,x)=(1,0) ? Zar griješim negdje? Jesam nešto krivo shvatila? :(
Ako mi netko može ovo objasniti jer ne vidim odgovor 
Na vježbama smo napisali da je {0,1}x Z lokalno konačan skup i da je
k([(a,b),(c,d)])⇐(d-b+1)*2
Sad meni nije jasno, nije li k( [(0,0),(1,0)])= aleph 0?
jer se "putuje" po drugoj varijabli (0,x) od (0,0) do (1,0) i kao tek u beskonačnosti postane (0,x)=(1,0) ? Zar griješim negdje? Jesam nešto krivo shvatila? 
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 14:18 čet, 6. 2. 2014 Naslov: Postano: 14:18 čet, 6. 2. 2014 Naslov: |
    |
|
|
U biti je jedini problematičan dio konstruirati sličnost između [latex]\mathbb{Q}\cap \langle 1, +\infty \rangle[/latex] i [latex]\mathbb{Q}\cap\langle \sqrt{2}, +\infty \rangle[/latex], ali zapravo ni ne trebamo jer su oba ta skupa slična s [latex]\mathbb{Q}[/latex].
Dakle postoji sličnost [latex]f:\mathbb{Q}\cap \langle \sqrt{2}, +\infty \rangle \to \mathbb{Q}\cap \langle 1, +\infty \rangle[/latex].
I sad sličnost između zadanih skupova definiramo ovako:
[latex]g:\mathbb{Q}\cup [0, \sqrt{2}] \to \mathbb{Q}\cup [0,1][/latex]
[latex]\begin{displaymath}
g(x) = \left\{
\begin{array}{lr}
x, & x \in \mathbb{Q}\cap \langle -\infty, 0 \rangle\\
\frac{x^2}{2}, & x \in [0, \sqrt{2}] \\
f(x), & x\in \mathbb{Q}\cap \langle \sqrt{2}, +\infty \rangle
\end{array}
\right
\end{displaymath}[/latex]
A kako točno definirati [latex]f[/latex], nemam pojma :D
Mene zanima može li mi neko raspisati korak indukcije u dokazu:
[latex]5+\alpha=\alpha, \; \alpha \geq \omega[/latex] (za [latex]\alpha[/latex] ordinalni broj)
U biti je jedini problematičan dio konstruirati sličnost između 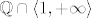 i i 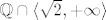 , ali zapravo ni ne trebamo jer su oba ta skupa slična s , ali zapravo ni ne trebamo jer su oba ta skupa slična s 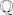 . .
Dakle postoji sličnost 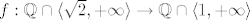 . .
I sad sličnost između zadanih skupova definiramo ovako:
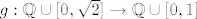
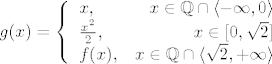
A kako točno definirati  , nemam pojma , nemam pojma 
Mene zanima može li mi neko raspisati korak indukcije u dokazu:
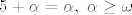 (za (za  ordinalni broj) ordinalni broj)
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 14:46 čet, 6. 2. 2014 Naslov: Postano: 14:46 čet, 6. 2. 2014 Naslov: |
    |
|
|
[quote="nuclear"]Ako mi netko može ovo objasniti jer ne vidim odgovor :D
Na vježbama smo napisali da je {0,1}x Z lokalno konačan skup i da je
k([(a,b),(c,d)])<=(d-b+1)*2
Sad meni nije jasno, nije li k( [(0,0),(1,0)])= aleph 0?
jer se "putuje" po drugoj varijabli (0,x) od (0,0) do (1,0) i kao tek u beskonačnosti postane (0,x)=(1,0) ? Zar griješim negdje? Jesam nešto krivo shvatila? :([/quote]
Ajmo pomalo. :)
Prvo definicije:
[tex]\{0,1\}\times\mathbb{Z}=\{(x,y) \mid x\in\{0,1\} \land y\in\mathbb{Z}\}[/tex]
Za proizvoljne [tex](x_1,y_1),(x_2,y_2)\in\{0,1\}\times\mathbb{Z}[/tex] relacija antileksikografskog uređaja je definirana na sljedeći način:
[tex](x_1,y_1)\mathop{<_{al}\,}(x_2,y_2) \stackrel{\mathrm{def}}{\iff} y_1 < y_2 \lor (y_1 = y_2 \land x_1 < x_2)[/tex].
E, sad, ako uzmemo proizvoljne [tex](a,b),(c,d)\in\{0,1\}\times\mathbb{Z}[/tex] za koje vrijedi [tex](a,b)\mathop{<_{al}\,}(c,d)[/tex], pitanje je koliko ima parova [tex](x,y)\in\{0,1\}\times\mathbb{Z}[/tex] takvih da je [tex](a,b)\mathop{<_{al}\,}(x,y)\mathop{<_{al}\,}(c,d)[/tex].
Gore navedeno svojstvo može biti zadovoljeno na ukupno četiri načina (po dva za svaku nejednakost). Promotrimo koji su to slučajevi:
1. [tex]b < y < d[/tex]. Kako su [tex]y[/tex], [tex]b[/tex] i [tex]d[/tex] cijeli brojevi, [tex]y[/tex] možemo odabrati na [tex]d-b-1[/tex] načina. Što s [tex]x[/tex]-evima? Na [tex]x[/tex] nemamo nikakve restrikcije, no izbor vrijednosti nam je ograničen na 0 i 1. Prema tome, za svaki [tex]y[/tex], [tex]x[/tex] možemo odabrati na dva različita načina. Konačno, ovaj slučaj zadovoljava [tex]2(d-b-1)[/tex] parova.
2. [tex]b = y < d \land a < x[/tex]. Vrijednost od [tex]y[/tex] nam je fiksirana, pa je jedino pitanje koliko [tex]x[/tex]-eva zadovoljava [tex]a<x[/tex]. Budući da su [tex]a,x\in\{0,1\}[/tex], odgovor je nijedan ako je [tex]a=1[/tex], a 1 ako je [tex]a=0[/tex]. Maksimalni broj parova u ovom slučaju je 1.
3. [tex]b < y = d \land x < c[/tex]. Analogno prethodnom slučaju, maksimalni broj parova koji ovo zadovoljavaju je 1.
4. [tex]b = y = d \land a < x < c[/tex]. Kako su [tex]x,a,c\in\{0,1\}[/tex] ovaj slučaj nije moguće zadovoljiti.
Uoči da je u svakom slučaju broj elemenata u intervalu [tex]\langle(a,b),(c,d)\rangle[/tex] konačan. Ako te zanimaju segmenti, stvar i dalje ostaje konačna, jer dodaješ samo dva nova elementa.
| nuclear (napisa): | Ako mi netko može ovo objasniti jer ne vidim odgovor 
Na vježbama smo napisali da je {0,1}x Z lokalno konačan skup i da je
k([(a,b),(c,d)])⇐(d-b+1)*2
Sad meni nije jasno, nije li k( [(0,0),(1,0)])= aleph 0?
jer se "putuje" po drugoj varijabli (0,x) od (0,0) do (1,0) i kao tek u beskonačnosti postane (0,x)=(1,0) ? Zar griješim negdje? Jesam nešto krivo shvatila?  |
Ajmo pomalo. 
Prvo definicije:
[tex]\{0,1\}\times\mathbb{Z}=\{(x,y) \mid x\in\{0,1\} \land y\in\mathbb{Z}\}[/tex]
Za proizvoljne [tex](x_1,y_1),(x_2,y_2)\in\{0,1\}\times\mathbb{Z}[/tex] relacija antileksikografskog uređaja je definirana na sljedeći način:
[tex](x_1,y_1)\mathop{<_{al}\,}(x_2,y_2) \stackrel{\mathrm{def}}{\iff} y_1 < y_2 \lor (y_1 = y_2 \land x_1 < x_2)[/tex].
E, sad, ako uzmemo proizvoljne [tex](a,b),(c,d)\in\{0,1\}\times\mathbb{Z}[/tex] za koje vrijedi [tex](a,b)\mathop{<_{al}\,}(c,d)[/tex], pitanje je koliko ima parova [tex](x,y)\in\{0,1\}\times\mathbb{Z}[/tex] takvih da je [tex](a,b)\mathop{<_{al}\,}(x,y)\mathop{<_{al}\,}(c,d)[/tex].
Gore navedeno svojstvo može biti zadovoljeno na ukupno četiri načina (po dva za svaku nejednakost). Promotrimo koji su to slučajevi:
1. [tex]b < y < d[/tex]. Kako su [tex]y[/tex], [tex]b[/tex] i [tex]d[/tex] cijeli brojevi, [tex]y[/tex] možemo odabrati na [tex]d-b-1[/tex] načina. Što s [tex]x[/tex]-evima? Na [tex]x[/tex] nemamo nikakve restrikcije, no izbor vrijednosti nam je ograničen na 0 i 1. Prema tome, za svaki [tex]y[/tex], [tex]x[/tex] možemo odabrati na dva različita načina. Konačno, ovaj slučaj zadovoljava [tex]2(d-b-1)[/tex] parova.
2. [tex]b = y < d \land a < x[/tex]. Vrijednost od [tex]y[/tex] nam je fiksirana, pa je jedino pitanje koliko [tex]x[/tex]-eva zadovoljava [tex]a<x[/tex]. Budući da su [tex]a,x\in\{0,1\}[/tex], odgovor je nijedan ako je [tex]a=1[/tex], a 1 ako je [tex]a=0[/tex]. Maksimalni broj parova u ovom slučaju je 1.
3. [tex]b < y = d \land x < c[/tex]. Analogno prethodnom slučaju, maksimalni broj parova koji ovo zadovoljavaju je 1.
4. [tex]b = y = d \land a < x < c[/tex]. Kako su [tex]x,a,c\in\{0,1\}[/tex] ovaj slučaj nije moguće zadovoljiti.
Uoči da je u svakom slučaju broj elemenata u intervalu [tex]\langle(a,b),(c,d)\rangle[/tex] konačan. Ako te zanimaju segmenti, stvar i dalje ostaje konačna, jer dodaješ samo dva nova elementa.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
nuclear
Forumaš(ica)


Pridružen/a: 13. 11. 2011. (17:40:12)
Postovi: (74)16
Spol: 
|
 Postano: 14:48 čet, 6. 2. 2014 Naslov: Postano: 14:48 čet, 6. 2. 2014 Naslov: |
    |
|
|
Ja se nikad neću naviknuti na ove DUS-ove :D
Opet nejasnoća s vježbi:
Zad 3.176
Neka je A podskup R (realni brojevi) DUS sa naslijeđenim standardnim uređajem iz R, dokaži da je k(A)<=aleph0
Muči me rješenje koje nam je dao asistent, na početku mi piše: "ako uzmemo N,Z,Q, dobivamo traženo"
...no ne vrijedi li da (Z,<) i (Q,<) nisu DUS-ovi?
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="mdoko"]
Ajmo pomalo. :)
.........[/quote]
Ono što je mene tu mučilo (inače hvala, shvatila sam o čemu se radi čim ste spomenuli antileksikografski) je da sam ja na to sve gledala preko leksikografskog uređaja :)
Ja se nikad neću naviknuti na ove DUS-ove 
Opet nejasnoća s vježbi:
Zad 3.176
Neka je A podskup R (realni brojevi) DUS sa naslijeđenim standardnim uređajem iz R, dokaži da je k(A)⇐aleph0
Muči me rješenje koje nam je dao asistent, na početku mi piše: "ako uzmemo N,Z,Q, dobivamo traženo"
...no ne vrijedi li da (Z,<) i (Q,<) nisu DUS-ovi?
Added after 1 minutes:
| mdoko (napisa): |
Ajmo pomalo. 
......... |
Ono što je mene tu mučilo (inače hvala, shvatila sam o čemu se radi čim ste spomenuli antileksikografski) je da sam ja na to sve gledala preko leksikografskog uređaja 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 15:08 čet, 6. 2. 2014 Naslov: Postano: 15:08 čet, 6. 2. 2014 Naslov: |
    |
|
|
[quote="Loo"]U biti je jedini problematičan dio konstruirati sličnost između [latex]\mathbb{Q}\cap \langle 1, +\infty \rangle[/latex] i [latex]\mathbb{Q}\cap\langle \sqrt{2}, +\infty \rangle[/latex], ali zapravo ni ne trebamo jer su oba ta skupa slična s [latex]\mathbb{Q}[/latex].
Dakle postoji sličnost [latex]f:\mathbb{Q}\cap \langle \sqrt{2}, +\infty \rangle \to \mathbb{Q}\cap \langle 1, +\infty \rangle[/latex].
I sad sličnost između zadanih skupova definiramo ovako:
[latex]g:\mathbb{Q}\cup [0, \sqrt{2}] \to \mathbb{Q}\cup [0,1][/latex]
[latex]\begin{displaymath}
g(x) = \left\{
\begin{array}{lr}
x, & x \in \mathbb{Q}\cap \langle -\infty, 0 \rangle\\
\frac{x^2}{2}, & x \in [0, \sqrt{2}] \\
f(x), & x\in \mathbb{Q}\cap \langle \sqrt{2}, +\infty \rangle
\end{array}
\right
\end{displaymath}[/latex]
A kako točno definirati [latex]f[/latex], nemam pojma :D
[/quote]
Nije ni bitno kako to definirati. Sve što nam treba je egzistencija, a ne eksplicitna konstrukcija.
[quote]Mene zanima može li mi neko raspisati korak indukcije u dokazu:
[latex]5+\alpha=\alpha, \; \alpha \geq \omega[/latex] (za [latex]\alpha[/latex] ordinalni broj)[/quote]
Evo, mogu ja. :wink:
Baza ([tex]5+\omega=\omega[/tex]) je poprilično jednostavna za dokazati.
Kad imamo bazu, korak izgleda ovako:
Neka je [tex]\alpha>\omega[/tex] takav da za svaki ordinal [tex]\beta\in[\omega,\alpha\rangle[/tex] vrijedi [tex]5+\beta=\beta[/tex]. Imamo dva slučaja.
1. [tex]\alpha[/tex] je sljedbenik, tj. postoji [tex]\delta[/tex] takav da je [tex]\alpha = \delta + 1[/tex]. Uočimo da je [tex]\delta\in[\omega,\alpha\rangle[/tex]. Sada imamo [tex]5+\alpha=5+(\delta+1)=(5+\delta)+1\stackrel{\mathrm{(IH)}}{=}\delta+1 =\alpha[/tex]
2. [tex]\alpha[/tex] je granični ordinal, tj. [tex]\alpha=\sup\{\delta\mid\delta<\alpha\}[/tex]. Koristeći činjenicu da je [tex]\alpha>\omega[/tex], vidimo da vrijedi [tex]\alpha=\sup\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex].
Sada imamo [tex]5+\alpha=5+\sup\{\delta\mid\omega\leqslant\delta<\alpha\}=\sup\{5+\delta\mid\omega\leqslant\delta<\alpha\}\stackrel{\mathrm{(IH)}}{=}\sup\{\delta\mid\omega\leqslant\delta<\alpha\}=\alpha[/tex].
Mjesta na kojima se koristi pretpostavka indukcije označena su sa (IH).
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="nuclear"]Ja se nikad neću naviknuti na ove DUS-ove :D
Opet nejasnoća s vježbi:
Zad 3.176
Neka je A podskup R (realni brojevi) DUS sa naslijeđenim standardnim uređajem iz R, dokaži da je k(A)<=aleph0
Muči me rješenje koje nam je dao asistent, na početku mi piše: "ako uzmemo N,Z,Q, dobivamo traženo"
...no ne vrijedi li da (Z,<) i (Q,<) nisu DUS-ovi?
[/quote]
U pravu si. Nisam siguran što se hoće s tim.
[quote]
[quote="mdoko"]
Ajmo pomalo. :)
.........[/quote]
Ono što je mene tu mučilo (inače hvala, shvatila sam o čemu se radi čim ste spomenuli antileksikografski) je da sam ja na to sve gledala preko leksikografskog uređaja :)[/quote]
Vrlo bitna stvar: defaultni produktni uređaj je [u]antileksikografski[/u].
| Loo (napisa): | U biti je jedini problematičan dio konstruirati sličnost između 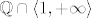 i i 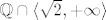 , ali zapravo ni ne trebamo jer su oba ta skupa slična s , ali zapravo ni ne trebamo jer su oba ta skupa slična s 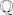 . .
Dakle postoji sličnost 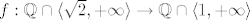 . .
I sad sličnost između zadanih skupova definiramo ovako:
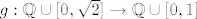
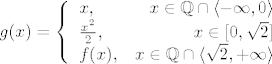
A kako točno definirati  , nemam pojma , nemam pojma 
|
Nije ni bitno kako to definirati. Sve što nam treba je egzistencija, a ne eksplicitna konstrukcija.
| Citat: | Mene zanima može li mi neko raspisati korak indukcije u dokazu:
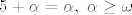 (za (za  ordinalni broj) ordinalni broj) |
Evo, mogu ja. 
Baza ([tex]5+\omega=\omega[/tex]) je poprilično jednostavna za dokazati.
Kad imamo bazu, korak izgleda ovako:
Neka je [tex]\alpha>\omega[/tex] takav da za svaki ordinal [tex]\beta\in[\omega,\alpha\rangle[/tex] vrijedi [tex]5+\beta=\beta[/tex]. Imamo dva slučaja.
1. [tex]\alpha[/tex] je sljedbenik, tj. postoji [tex]\delta[/tex] takav da je [tex]\alpha = \delta + 1[/tex]. Uočimo da je [tex]\delta\in[\omega,\alpha\rangle[/tex]. Sada imamo [tex]5+\alpha=5+(\delta+1)=(5+\delta)+1\stackrel{\mathrm{(IH)}}{=}\delta+1 =\alpha[/tex]
2. [tex]\alpha[/tex] je granični ordinal, tj. [tex]\alpha=\sup\{\delta\mid\delta<\alpha\}[/tex]. Koristeći činjenicu da je [tex]\alpha>\omega[/tex], vidimo da vrijedi [tex]\alpha=\sup\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex].
Sada imamo [tex]5+\alpha=5+\sup\{\delta\mid\omega\leqslant\delta<\alpha\}=\sup\{5+\delta\mid\omega\leqslant\delta<\alpha\}\stackrel{\mathrm{(IH)}}{=}\sup\{\delta\mid\omega\leqslant\delta<\alpha\}=\alpha[/tex].
Mjesta na kojima se koristi pretpostavka indukcije označena su sa (IH).
Added after 3 minutes:
| nuclear (napisa): | Ja se nikad neću naviknuti na ove DUS-ove 
Opet nejasnoća s vježbi:
Zad 3.176
Neka je A podskup R (realni brojevi) DUS sa naslijeđenim standardnim uređajem iz R, dokaži da je k(A)⇐aleph0
Muči me rješenje koje nam je dao asistent, na početku mi piše: "ako uzmemo N,Z,Q, dobivamo traženo"
...no ne vrijedi li da (Z,<) i (Q,<) nisu DUS-ovi?
|
U pravu si. Nisam siguran što se hoće s tim.
| Citat: |
| mdoko (napisa): |
Ajmo pomalo. 
......... |
Ono što je mene tu mučilo (inače hvala, shvatila sam o čemu se radi čim ste spomenuli antileksikografski) je da sam ja na to sve gledala preko leksikografskog uređaja  |
Vrlo bitna stvar: defaultni produktni uređaj je antileksikografski.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
stara
Forumaš(ica)

Pridružen/a: 06. 02. 2014. (15:27:38)
Postovi: (4)16
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 16:46 čet, 6. 2. 2014 Naslov: Postano: 16:46 čet, 6. 2. 2014 Naslov: |
    |
|
|
[quote="stara"]Može li netko lijepo raspisati šesti zadatak, s invarijantom sličnosti?
Zadatak glasi : Dokažite da je " biti sličan s nekim svojim pravim podskupom " invarijanta sličnosti za TUSove.[/quote]
Neka su [tex](A,<)[/tex] i [tex](B,\prec)[/tex] slični totalno uređeni skupovi, te neka je [tex]X\subset A[/tex] takav da je [tex](X,<)\simeq(A,<)[/tex].
Iz gornjih pretpostavki slijedi da postoje sličnosti [tex]f\colon A \to B[/tex] i [tex]\varphi\colon A\to X[/tex].
Uočimo da je [tex]Y\stackrel{\mathrm{def}}{=}f^{\to}(X) \subset B[/tex]. (Mora biti pravi podskup jer se radi o slici pravog podskupa dobivenog putem bijekcije.)
Sada definiramo [tex]\psi\colon B \to Y[/tex], [tex]\psi(b) \stackrel{\mathrm{def}}{=} f\left(\varphi\left(f^{-1}(b)\right)\right)[/tex].
[tex]\psi[/tex] je očito bijekcija jer je kompozicija triju bijekcija. Sve što je preostalo dokazati je da [tex]\psi[/tex] čuva uređaj. U tu svrhu, neka su [tex]b_1,b_2\in B[/tex] za koje vrijedi [tex]b_1\prec b_2[/tex]. Kako je [tex]f[/tex] sličnost, imamo [tex]f^{-1}(b_1)<f^{-1}(b_2)[/tex]. Sada koristeći činjenicu da je [tex]\varphi[/tex] sličnost, dobivamo [tex]\varphi\left(f^{-1}(b_1)\right)<\varphi\left(f^{-1}(b_2)\right)[/tex]. Konačno, još jednom upotrebom činjenice da je [tex]f[/tex] sličnost, slijedi [tex] f\left(\varphi\left(f^{-1}(b_1)\right)\right)\prec f\left(\varphi\left(f^{-1}(b_2)\right)\right)[/tex], odnosno [tex]\psi(b_1)\prec\psi(b_2)[/tex].
Ovime je dokazana tvrdnja zadatka.
[size=9][color=#999999]Added after 13 minutes:[/color][/size]
[quote="Loo"][quote="mdoko"]
2. [tex]\alpha[/tex] je granični ordinal, tj. [tex]\alpha=\sup\{\delta\mid\delta<\alpha\}[/tex]. Koristeći činjenicu da je [tex]\alpha>\omega[/tex], vidimo da vrijedi [tex]\alpha=\sup\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex].
[/quote]
E baš me ovaj dio mučio. Jako je očito da to vrijedi, ali nisam sigurna kako bi to detaljno raspisala. Treba li uopće?[/quote]
Nisam baš siguran što znači "treba li". Formalno treba, ali je poprilično trivijalno. Radi potpunosti neka i to bude ovdje.
Neka je [tex]\alpha > \omega[/tex]. Valjanost sljedeće formule je valjda očita (ako nije raspisat ću): [tex]\forall\gamma\big((\forall\zeta\in[0,\alpha\rangle)(\zeta\leqslant\gamma)\leftrightarrow(\forall\zeta\in[\omega,\alpha\rangle)(\zeta\leqslant\gamma)\big)[/tex]. Prema tome, [tex]\gamma[/tex] je gornja međa skupa [tex]\{\delta\mid\delta<\alpha\}[/tex], ako i samo ako je ujedno i gornja međa skupa [tex]\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex]. Dakle, najmanja gornja međa skupa [tex]\{\delta\mid\delta<\alpha\}[/tex] jednaka je najmanjoj gornjoj međi skupa [tex]\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex].
| stara (napisa): | Može li netko lijepo raspisati šesti zadatak, s invarijantom sličnosti?
Zadatak glasi : Dokažite da je " biti sličan s nekim svojim pravim podskupom " invarijanta sličnosti za TUSove. |
Neka su [tex](A,<)[/tex] i [tex](B,\prec)[/tex] slični totalno uređeni skupovi, te neka je [tex]X\subset A[/tex] takav da je [tex](X,<)\simeq(A,<)[/tex].
Iz gornjih pretpostavki slijedi da postoje sličnosti [tex]f\colon A \to B[/tex] i [tex]\varphi\colon A\to X[/tex].
Uočimo da je [tex]Y\stackrel{\mathrm{def}}{=}f^{\to}(X) \subset B[/tex]. (Mora biti pravi podskup jer se radi o slici pravog podskupa dobivenog putem bijekcije.)
Sada definiramo [tex]\psi\colon B \to Y[/tex], [tex]\psi(b) \stackrel{\mathrm{def}}{=} f\left(\varphi\left(f^{-1}(b)\right)\right)[/tex].
[tex]\psi[/tex] je očito bijekcija jer je kompozicija triju bijekcija. Sve što je preostalo dokazati je da [tex]\psi[/tex] čuva uređaj. U tu svrhu, neka su [tex]b_1,b_2\in B[/tex] za koje vrijedi [tex]b_1\prec b_2[/tex]. Kako je [tex]f[/tex] sličnost, imamo [tex]f^{-1}(b_1)<f^{-1}(b_2)[/tex]. Sada koristeći činjenicu da je [tex]\varphi[/tex] sličnost, dobivamo [tex]\varphi\left(f^{-1}(b_1)\right)<\varphi\left(f^{-1}(b_2)\right)[/tex]. Konačno, još jednom upotrebom činjenice da je [tex]f[/tex] sličnost, slijedi [tex] f\left(\varphi\left(f^{-1}(b_1)\right)\right)\prec f\left(\varphi\left(f^{-1}(b_2)\right)\right)[/tex], odnosno [tex]\psi(b_1)\prec\psi(b_2)[/tex].
Ovime je dokazana tvrdnja zadatka.
Added after 13 minutes:
| Loo (napisa): | | mdoko (napisa): |
2. [tex]\alpha[/tex] je granični ordinal, tj. [tex]\alpha=\sup\{\delta\mid\delta<\alpha\}[/tex]. Koristeći činjenicu da je [tex]\alpha>\omega[/tex], vidimo da vrijedi [tex]\alpha=\sup\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex].
|
E baš me ovaj dio mučio. Jako je očito da to vrijedi, ali nisam sigurna kako bi to detaljno raspisala. Treba li uopće? |
Nisam baš siguran što znači "treba li". Formalno treba, ali je poprilično trivijalno. Radi potpunosti neka i to bude ovdje.
Neka je [tex]\alpha > \omega[/tex]. Valjanost sljedeće formule je valjda očita (ako nije raspisat ću): [tex]\forall\gamma\big((\forall\zeta\in[0,\alpha\rangle)(\zeta\leqslant\gamma)\leftrightarrow(\forall\zeta\in[\omega,\alpha\rangle)(\zeta\leqslant\gamma)\big)[/tex]. Prema tome, [tex]\gamma[/tex] je gornja međa skupa [tex]\{\delta\mid\delta<\alpha\}[/tex], ako i samo ako je ujedno i gornja međa skupa [tex]\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex]. Dakle, najmanja gornja međa skupa [tex]\{\delta\mid\delta<\alpha\}[/tex] jednaka je najmanjoj gornjoj međi skupa [tex]\{\delta\mid\omega\leqslant\delta<\alpha\}[/tex].
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
malisputnik
Forumaš(ica)
Pridružen/a: 02. 09. 2013. (08:43:21)
Postovi: (31)16
|
 Postano: 18:14 čet, 6. 2. 2014 Naslov: Postano: 18:14 čet, 6. 2. 2014 Naslov: |
    |
|
|
[tex]\alpha[/tex] i [tex]\beta[/tex] su ordinali i treba dokazati sljedece:
[tex]\alpha <\beta \quad \vee \quad \alpha = \beta \quad \vee \quad \beta < \alpha [/tex]?
Moze li netto raspisati za [tex]\alpha[/tex] je sljedbenik i granicni?
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="matijaB"]Jel moze pomoc kod dokaza ove prop
bilo koji broj da rijesi [url]http://i.imgur.com/hKvUtFU.png[/url]
1 ili 2 bi bilo najbolje :D[/quote]
prvi je rjesio mdoko.
[quote="mdoko"][quote="moni_poni"]Može li netko dokazati sa str.40. propoziciju 1.54. (bilo koju tvdnju)?
http://web.math.pmf.unizg.hr/~vukovic/Diplomski-kolegiji/TS/TS-skripta-2013.pdf[/quote]
Neka je [tex]a = \mathop{\mathrm{card}} A[/tex], [tex]b = \mathop{\mathrm{card}} B[/tex] i [tex]c = \mathop{\mathrm{card}} C[/tex]. Dokažimo da vrijedi [tex]a^b\cdot a^c = a^{b+c}[/tex].
Iz definicija aritmetičkih operacija nad kardinalnim brojevima, imamo ([color=red]ako ti ovo nije očito, raspiši[/color]) [tex]a^b\cdot a^c = \mathop{\mathrm{card}}\left( {}^BA \times {}^CA \right)[/tex] i [tex]a^{b+c} = \mathop{\mathrm{card}} \left( {}^{(B\times\{0\})\cup(C\times\{1\})}A \right)[/tex].
Da dokažemo traženu jednakost, dovoljno je dokazati postojanje bijekcije među skupovima [tex]\left( {}^BA \times {}^CA \right)[/tex] i [tex]{}^{(B\times\{0\})\cup(C\times\{1\})}A[/tex]. Jedna takva bijekcija je ([color=red]uvjeri se da se uistinu radi o bijekciji[/color]):
[tex] \Phi\colon \left( {}^BA \times {}^CA \right) \to {}^{(B\times\{0\})\cup(C\times\{1\})}A [/tex], pri čemu je za proizvoljne funkcije [tex]f\colon B\to A[/tex] i [tex]g\colon C\to A[/tex], te proizvoljne [tex]x\in B\cup C[/tex] i [tex]i \in \{0,1\}[/tex], [tex]\left(\Phi(f,g)\right)(x,i)=\left\{\begin{array}{ccc} f(x) & \textrm{ako je} & i=0 \\ g(x) & \textrm{ako je} &i=1\end{array}\right.[/tex].
(Uoči da je [tex]\Phi[/tex] funkcija koja paru funkcija [tex](f\colon B\to A,g\colon C\to A)[/tex] pridružuje funkciju [tex]h\colon(B\times\{0\})\cup(C\times\{1\})\to A[/tex].)[/quote]
[tex]\alpha[/tex] i [tex]\beta[/tex] su ordinali i treba dokazati sljedece:
[tex]\alpha <\beta \quad \vee \quad \alpha = \beta \quad \vee \quad \beta < \alpha [/tex]?
Moze li netto raspisati za [tex]\alpha[/tex] je sljedbenik i granicni?
Added after 1 minutes:
prvi je rjesio mdoko.
| mdoko (napisa): |
Neka je [tex]a = \mathop{\mathrm{card}} A[/tex], [tex]b = \mathop{\mathrm{card}} B[/tex] i [tex]c = \mathop{\mathrm{card}} C[/tex]. Dokažimo da vrijedi [tex]a^b\cdot a^c = a^{b+c}[/tex].
Iz definicija aritmetičkih operacija nad kardinalnim brojevima, imamo (ako ti ovo nije očito, raspiši) [tex]a^b\cdot a^c = \mathop{\mathrm{card}}\left( {}^BA \times {}^CA \right)[/tex] i [tex]a^{b+c} = \mathop{\mathrm{card}} \left( {}^{(B\times\{0\})\cup(C\times\{1\})}A \right)[/tex].
Da dokažemo traženu jednakost, dovoljno je dokazati postojanje bijekcije među skupovima [tex]\left( {}^BA \times {}^CA \right)[/tex] i [tex]{}^{(B\times\{0\})\cup(C\times\{1\})}A[/tex]. Jedna takva bijekcija je (uvjeri se da se uistinu radi o bijekciji):
[tex] \Phi\colon \left( {}^BA \times {}^CA \right) \to {}^{(B\times\{0\})\cup(C\times\{1\})}A [/tex], pri čemu je za proizvoljne funkcije [tex]f\colon B\to A[/tex] i [tex]g\colon C\to A[/tex], te proizvoljne [tex]x\in B\cup C[/tex] i [tex]i \in \{0,1\}[/tex], [tex]\left(\Phi(f,g)\right)(x,i)=\left\{\begin{array}{ccc} f(x) & \textrm{ako je} & i=0 \\ g(x) & \textrm{ako je} &i=1\end{array}\right.[/tex].
(Uoči da je [tex]\Phi[/tex] funkcija koja paru funkcija [tex](f\colon B\to A,g\colon C\to A)[/tex] pridružuje funkciju [tex]h\colon(B\times\{0\})\cup(C\times\{1\})\to A[/tex].) |
|
|
| [Vrh] |
|
stara
Forumaš(ica)

Pridružen/a: 06. 02. 2014. (15:27:38)
Postovi: (4)16
|
|
| [Vrh] |
|
|














