| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Rodman
Forumaš(ica)

Pridružen/a: 11. 09. 2003. (14:08:59)
Postovi: (18)16
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 22:04 pon, 13. 9. 2004 Naslov: Postano: 22:04 pon, 13. 9. 2004 Naslov: |
    |
|
|
:shock: ne volem limese a limesi bez l'h ne vole mene :shock:
..al jedna ideja koja mi upravo pade napamet jes da se okoristis L'Hospitalovim pravilom da doznas vrijednost limesa u 0 u nadi da ces zahvaljujuci tomu naci i metodu rjesavanja.
Direktna primjena toga bi bila da si znatno olaksas rjesavanje limesa pomocu npr. teorema o sendvicu ukoliko imas na umu slijedece relacije:
[latex]\sum_{i=1}^n \frac{x^n}{n!} \le e^x~, x>0~[/latex] (za x<0 suma nije monotona sa obzirom na n)
za neko (dovoljno) maleno n (npr. 2-3 clana je obicno dovoljno, ali ne nuzno)
ili (ova relacija se koristi u jednom od pocetnih dokaza u analizi 2):
[latex]\left ( 1 + \frac{x}{n} \right ) ^n \le e^x \le \left ( 1 + \frac{x}{n} \right ) ^{n+1}[/latex]
(gdje za n iz |N, opet, mozes uzeti neki dovoljno mali broj da ti da neku (dovoljno dobru) donju/gornju ogradu a da ti ne zakomplicira stvari u zadatku suvise)
sretno!
PS pitanje: kod razvoja e^x u Taylorov red oko 0 za x<0, da li (i za koje n-ove) se vrijednosti taylorovog reda drze "sa iste strane" u odnosu na vrijednosti od e^x ili ima npr. n1, n2 iz |N t.d. [latex]T_{n_1}(0;x) \le e^x \le T_{n_2}(0;x)[/latex] ?
 ne volem limese a limesi bez l'h ne vole mene ne volem limese a limesi bez l'h ne vole mene 
..al jedna ideja koja mi upravo pade napamet jes da se okoristis L'Hospitalovim pravilom da doznas vrijednost limesa u 0 u nadi da ces zahvaljujuci tomu naci i metodu rjesavanja.
Direktna primjena toga bi bila da si znatno olaksas rjesavanje limesa pomocu npr. teorema o sendvicu ukoliko imas na umu slijedece relacije:
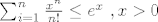 (za x<0 suma nije monotona sa obzirom na n) (za x<0 suma nije monotona sa obzirom na n)
za neko (dovoljno) maleno n (npr. 2-3 clana je obicno dovoljno, ali ne nuzno)
ili (ova relacija se koristi u jednom od pocetnih dokaza u analizi 2):
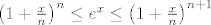
(gdje za n iz |N, opet, mozes uzeti neki dovoljno mali broj da ti da neku (dovoljno dobru) donju/gornju ogradu a da ti ne zakomplicira stvari u zadatku suvise)
sretno!
PS pitanje: kod razvoja e^x u Taylorov red oko 0 za x<0, da li (i za koje n-ove) se vrijednosti taylorovog reda drze "sa iste strane" u odnosu na vrijednosti od e^x ili ima npr. n1, n2 iz |N t.d. 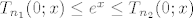 ? ?
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 10:45 uto, 14. 9. 2004 Naslov: Postano: 10:45 uto, 14. 9. 2004 Naslov: |
    |
|
|
[quote="Anonymous"]Što raditi s e? U biti, svede se na
lim (e^t -1)/t koji je jednak 1 kada t teži k 0. (*)
Može se na početku npr. oduzeti i dodati cos(3x) u brojniku. Rastavi se tada na dva razlomka, drugi vodi na limes tipa (sin ax/sin bx)^2 koji se lako rješava. Prvi razlomak je (e^(3x^2) - 1)/ (sin x)^2 koji nakon proširivanja s x^2 lako vodi na (*).[/quote]
Disklejmer: ovo vjerovatno nije najocitiji i najelementarniji nacin da se rijesi ovaj zadatak, ali evo ga (btw: nije li (e^t-1)/t "tablicni" limes?):
Hm, bravo :) Ako si dobila gornji izraz, onda bi, mozda, bilo uputno primijeniti gornju relaciju:
[latex]\left( 1 + \frac{t}{n} \right) ^n \le e^t \leq \left( 1 + \frac{t}{n} \right) ^{n+1}[/latex]
i uvrstit ju za n=1 u onaj limes (po teoremu o sendvicu):
[latex]\lim_{t \rightarrow 0} \frac{1 + t - 1}{t}
\leq \lim_{t \rightarrow 0} \frac{e^t -1}{t} [/latex]
Gornja ograda je zeznutija, al dosta lijepa. Imamo (po Binomnom teoremu):
[latex]\newcommand{\combination}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\lim_{t \rightarrow 0} \frac{e^t -1}{t}
\leq \lim_{t \rightarrow 0} \left ( 1 + \frac{t}{n} \right ) ^{n+1} = \\
~ (*) ~\lim_{t \rightarrow 0} \frac{ 1 + \combination{n+1}{1}t/n + \combination{n+1}{2}(t/n)^2 + \cdots + \combination{n+1}{n+1}(t/n)^{n+1} - 1}{\displaystyle{t}}= \\=\lim_{t \rightarrow 0} \combination{n+1}{1}\frac{1}{n} + t*P(t) = \cdots[/latex]
gdje je P(t) neki polinom, ono sto u biti kazem gore jest: [i]"kada (*) pokratimo sa t iz nazivnika i izvucem prvi clan, ostaje mi taj prvi clan skracen za t i polinom iz kojeg mogu izluciti t"[/i]. Taj polinom ima limes u 0, kao i t i imamo 0*P(0)=0
[latex]\newcommand{\combination}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\cdots = \lim_{t \rightarrow 0} \combination{n+1}{1}\frac{1}{n}= \lim_{t \rightarrow 0} \frac{n+1}{n} ~, ~\forall n \in N[/latex]
..sto je, opet, po teoremu o sendvicu (al ovog puta za nizove) (a mozes se iskazati i preko 15. (Cantorovog) aksioma) jednako:
[latex] (*) \leq \lim_{t \rightarrow 0} \lim_{n \rightarrow \infty} \frac{n+1}{n}=\lim_{t \rightarrow 0} 1[/latex] :D
Postupak nije tako tezak kao sto izgleda, zapravo, u potpunosti je analogan slucaju sa donjom ogradom. Uzeli smo neke jaako velike n-ove i pokratili razlomak ;)
Tj. nakon kracenja smo dobili nesto sto ne ovisi o varijabli t i nesto sto konvergira u 0. Onda smo rijesili taj dio koji ne ovisi o t (tj onaj limes po n ;)) i dobili rjesenje :)
[quote="veky"]Već znaš odgovor na to pitanje. Hint: Leibnizov kriterij. ;-)[/quote]
Hm, da, [url=http://degiorgi.math.hr/forum/viewtopic.php?t=2619]istina[/url] :)
| Anonymous (napisa): | Što raditi s e? U biti, svede se na
lim (e^t -1)/t koji je jednak 1 kada t teži k 0. (*)
Može se na početku npr. oduzeti i dodati cos(3x) u brojniku. Rastavi se tada na dva razlomka, drugi vodi na limes tipa (sin ax/sin bx)^2 koji se lako rješava. Prvi razlomak je (e^(3x^2) - 1)/ (sin x)^2 koji nakon proširivanja s x^2 lako vodi na (*). |
Disklejmer: ovo vjerovatno nije najocitiji i najelementarniji nacin da se rijesi ovaj zadatak, ali evo ga (btw: nije li (e^t-1)/t "tablicni" limes?):
Hm, bravo  Ako si dobila gornji izraz, onda bi, mozda, bilo uputno primijeniti gornju relaciju: Ako si dobila gornji izraz, onda bi, mozda, bilo uputno primijeniti gornju relaciju:
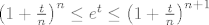
i uvrstit ju za n=1 u onaj limes (po teoremu o sendvicu):
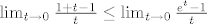
Gornja ograda je zeznutija, al dosta lijepa. Imamo (po Binomnom teoremu):
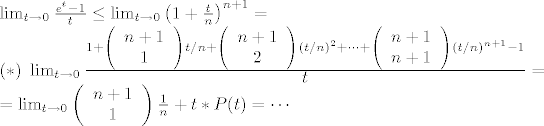
gdje je P(t) neki polinom, ono sto u biti kazem gore jest: "kada (*) pokratimo sa t iz nazivnika i izvucem prvi clan, ostaje mi taj prvi clan skracen za t i polinom iz kojeg mogu izluciti t". Taj polinom ima limes u 0, kao i t i imamo 0*P(0)=0
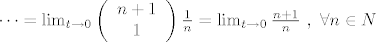
..sto je, opet, po teoremu o sendvicu (al ovog puta za nizove) (a mozes se iskazati i preko 15. (Cantorovog) aksioma) jednako:
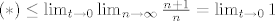 
Postupak nije tako tezak kao sto izgleda, zapravo, u potpunosti je analogan slucaju sa donjom ogradom. Uzeli smo neke jaako velike n-ove i pokratili razlomak 
Tj. nakon kracenja smo dobili nesto sto ne ovisi o varijabli t i nesto sto konvergira u 0. Onda smo rijesili taj dio koji ne ovisi o t (tj onaj limes po n  ) i dobili rjesenje ) i dobili rjesenje 
| veky (napisa): | Već znaš odgovor na to pitanje. Hint: Leibnizov kriterij.  |
Hm, da, istina 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
|





