| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
markann
Forumaš(ica)
Pridružen/a: 07. 10. 2013. (01:37:06)
Postovi: (1F)16
|
 Postano: 2:48 čet, 5. 6. 2014 Naslov: Postano: 2:48 čet, 5. 6. 2014 Naslov: |
    |
|
|
[quote="room"]Mene muči 2.19. d) i 2.20. b)[/quote]
2.19 d) se svodi na obicnu supstituciju [tex]t=arctgx[/tex] i kad se to malo sredi trebalo bi se dobit
[dtex]\int sinte^tdt[/dtex]
2.20 b) ... da. racionalne funkcije su malo zahtjevne za racunanje, ali ideja stvarno nije teska, i uvjek sve ide po istom postupku:
1) svest nazivnik na polinome 1. i 2. stupnja (da to mozemo nam tvrdi teorem iz em1, osim ako nemozemo nac nultocke, onda malo ideje)
2) rastaviti na parcijalne razlomke(jedan od meni najtezih djelova, jednom sam radio matricu da rjesim sustav) i upotrijebiti linearnost integrala
3) [tex]\int \frac{dx}{(Ax+B)^n}[/tex] za integrirati je trivijalno
4) kod kvadratnih polinoma nazivnik [tex]Cx^2+Dx+E[/tex] uvjek normirati prvo (dijeliti sa C) i onda namjestiti gornji polinom [tex]Ax+B[/tex] tako da dio bude derivacija od [tex]x^2+\frac{D}{C}x+\frac{E}{C}[/tex] a ostatak opet prosiriti po linearnosti
tj
[dtex]konstanta*\int \frac{2x+\frac{D}{C}+ostatak}{(x^2+\frac{D}{C}x+\frac{E}{C})^n}dx = konstanta*\int \frac{2x+\frac{D}{C}dx}{(x^2+\frac{D}{C}x+\frac{E}{C})^n} + konstanta*ostatak* \int \frac{dx}{(x^2+\frac{D}{C}x+\frac{E}{C})^n}[/dtex]
5) [tex]\int \frac{2x+\frac{D}{C}dx}{(x^2+\frac{D}{C}x+\frac{E}{C})^n}[/tex] je za integrirati trivijalno
6) sada nazivnik od zadnjeg integrala svedes na potpuni kvadrat (to nam opet garantira teorem jer je diskriminanta manja od 0 il nes nemam pojma) i to normirani u odnosu na konstantu bla bla bla dobijes
[dtex]konstanta*\int \frac{dt}{(t^2+1)^n}[/dtex]
primjer: konkretno u tom 2.20 b) ja sam dobio
[dtex](x^2-x+1)^2(x-1)^2[/dtex] uglavnom, pretpostavimo da sam raspisao sve to i dosao do
[dtex]K \int \frac{dx}{(x^2-x+1)^2} = K \int \frac{dx}{((x-1/2)^2+3/4)^2} = K \int \frac{dt}{(t^2+\frac{3}{4})^2} = K \frac{32}{9\sqrt{3}} \int \frac{ds}{(s^2+1)^2}[/dtex]
7) i pomocu parcijalne integracije dobijes rekurziju, al mislim ni nece ti trebat jer sumnjam da ce u zadacima ikad n biti veci od 2 ili 3..
uglavnom, da ima posla i racunanja, pogotovo meni kojemu je tesko zbrajati karte u beli, ali da to je to!
specijalno, za n=2 [tex]\int \frac{ds}{(s^2+1)^2}[/tex] vrijedi supstitucija [tex]t=arctgs[/tex] i dobijes
[dtex]\int \frac{ds}{(s^2+1)^2} = \int \frac{dt}{tg^2t+1} = \int cos^2t dt = \frac{1}{2} ( \int dt + \int cos2t dt) + C = \frac{1}{2} (arctgs + \frac{s}{1+s^2}) + C[/dtex]
PREKRASNO zar ne?
i onda umjesto s mozes uvrstit svoju prijasnju supstituciju i to je to.. Nadam se da sam barem malo pomogao
| room (napisa): | | Mene muči 2.19. d) i 2.20. b) |
2.19 d) se svodi na obicnu supstituciju [tex]t=arctgx[/tex] i kad se to malo sredi trebalo bi se dobit
[dtex]\int sinte^tdt[/dtex]
2.20 b) ... da. racionalne funkcije su malo zahtjevne za racunanje, ali ideja stvarno nije teska, i uvjek sve ide po istom postupku:
1) svest nazivnik na polinome 1. i 2. stupnja (da to mozemo nam tvrdi teorem iz em1, osim ako nemozemo nac nultocke, onda malo ideje)
2) rastaviti na parcijalne razlomke(jedan od meni najtezih djelova, jednom sam radio matricu da rjesim sustav) i upotrijebiti linearnost integrala
3) [tex]\int \frac{dx}{(Ax+B)^n}[/tex] za integrirati je trivijalno
4) kod kvadratnih polinoma nazivnik [tex]Cx^2+Dx+E[/tex] uvjek normirati prvo (dijeliti sa C) i onda namjestiti gornji polinom [tex]Ax+B[/tex] tako da dio bude derivacija od [tex]x^2+\frac{D}{C}x+\frac{E}{C}[/tex] a ostatak opet prosiriti po linearnosti
tj
[dtex]konstanta*\int \frac{2x+\frac{D}{C}+ostatak}{(x^2+\frac{D}{C}x+\frac{E}{C})^n}dx = konstanta*\int \frac{2x+\frac{D}{C}dx}{(x^2+\frac{D}{C}x+\frac{E}{C})^n} + konstanta*ostatak* \int \frac{dx}{(x^2+\frac{D}{C}x+\frac{E}{C})^n}[/dtex]
5) [tex]\int \frac{2x+\frac{D}{C}dx}{(x^2+\frac{D}{C}x+\frac{E}{C})^n}[/tex] je za integrirati trivijalno
6) sada nazivnik od zadnjeg integrala svedes na potpuni kvadrat (to nam opet garantira teorem jer je diskriminanta manja od 0 il nes nemam pojma) i to normirani u odnosu na konstantu bla bla bla dobijes
[dtex]konstanta*\int \frac{dt}{(t^2+1)^n}[/dtex]
primjer: konkretno u tom 2.20 b) ja sam dobio
[dtex](x^2-x+1)^2(x-1)^2[/dtex] uglavnom, pretpostavimo da sam raspisao sve to i dosao do
[dtex]K \int \frac{dx}{(x^2-x+1)^2} = K \int \frac{dx}{((x-1/2)^2+3/4)^2} = K \int \frac{dt}{(t^2+\frac{3}{4})^2} = K \frac{32}{9\sqrt{3}} \int \frac{ds}{(s^2+1)^2}[/dtex]
7) i pomocu parcijalne integracije dobijes rekurziju, al mislim ni nece ti trebat jer sumnjam da ce u zadacima ikad n biti veci od 2 ili 3..
uglavnom, da ima posla i racunanja, pogotovo meni kojemu je tesko zbrajati karte u beli, ali da to je to!
specijalno, za n=2 [tex]\int \frac{ds}{(s^2+1)^2}[/tex] vrijedi supstitucija [tex]t=arctgs[/tex] i dobijes
[dtex]\int \frac{ds}{(s^2+1)^2} = \int \frac{dt}{tg^2t+1} = \int cos^2t dt = \frac{1}{2} ( \int dt + \int cos2t dt) + C = \frac{1}{2} (arctgs + \frac{s}{1+s^2}) + C[/dtex]
PREKRASNO zar ne?
i onda umjesto s mozes uvrstit svoju prijasnju supstituciju i to je to.. Nadam se da sam barem malo pomogao
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
markann
Forumaš(ica)
Pridružen/a: 07. 10. 2013. (01:37:06)
Postovi: (1F)16
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
markann
Forumaš(ica)
Pridružen/a: 07. 10. 2013. (01:37:06)
Postovi: (1F)16
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
 Postano: 2:24 sub, 7. 6. 2014 Naslov: Postano: 2:24 sub, 7. 6. 2014 Naslov: |
    |
|
|
Ajme hvala ti puno, napokon sam ga uspjela do kraja i točan je. :D (dođe mi da plačem od sreće što sam ga napokon dovršila hahaha)
Još uvijek mi ovo objašnjenje treba ako netko zna:
[quote="room"]
EDIT: Ipak još jedno pitanje.
http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_7.pdf
Zadatak 2.62. je riješen u skriptici, ali nije na vježbama. I nije mi baš jasno kako su ga riješili. Shvatila bih ovaj prvi dio jednakosti koji gleda integral sa granicama -3 do -2, ali ne znam zašto je drugačiji polinom nego zadani. A nastavak jednakosti mi nije jasan zašto je uopće tu i kako smo to gledali.
Ovo je graf u wa: http://www.wolframalpha.com/input/?i=y%3Dx%5E2-x-6%2C+y%3D0%2C[/quote]
I iz ove skriptice 2.35. a) i b): http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_3.pdf
2.35. a) ne znam kako bi, a 2.35. b) sam došla do jednog dijela pa sam zapela.. Podijelila sam polinome i ono što sam mogla sam integrirala.
[dtex]\frac{x^2}{2}+x+\int \frac{4x^3+4x^2-4x-6}{(x^2-2)^2}dx[/dtex]
I sad sam ovaj integral razdvojila ovako:
[dtex]4\int\frac{x^3}{(x^2-2)^2}dx+4\int\frac{x^2}{(x^2-2)^2}dx-4\int\frac{x}{(x^2-2)^2}dx-6\int\frac{1}{(x^2-2)^2}dx[/dtex]
Drugi i treći integral sam sredila i provjerila s wolfram alphom. No prvi i četvrti me muče. Četvrti ne znam kako bih, a prvi mi se u jednoj stvari razlikuje sa wolframom alphom pa mi recite di sam fulala..
[dtex]4\int\frac{x^3}{(x^2-2)^2}dx= [u=x^2, du=2xdx, dv=\frac{xdx}{(x^2-2)^2}, v=\frac{-1}{2(x^2-2)}] =\frac{-2x^2}{x^2-2}+4\int\frac{xdx}{x^2-2} = \frac{-2x^2}{x^2-2}+4\int\frac{\frac{dt}{2}}{t} = \frac{-2x^2}{x^2-2}+2ln(x^2-2)[/dtex]
I sad wolfram alpha logaritam dobije isto, ali ovo ispred dobije: [dtex]\frac{-4}{x^2-2}[/dtex]
Di je greška? :oops:
[quote="pllook"]može li mi netko pomoći sa ovim zadacima?
2.34. a), 2.35. b) http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_3.pdf[/quote]
2.34. a) imam.
Prvo na parcijalne razlomke razdvojiš, zatim napraviš supstituciju t=arctgx, pa tangense raspišeš kao sin/cos, pa ćeš dobiti cos^2, to napišeš kao [tex]\frac{1+cos2t}{2}[/tex] i cos^4, to napišeš kao [tex]\frac{1}{8}(cos4t+4cos2t+3)[/tex] i onda svaki posebno razdvojiš i integriraš i vratiš nazad iz t u x.
Ako treba neki dio raspisat skroz ili provjerit, reci (sad mi je prekasno bilo da i to sve raspisujem :? ).
Ajme hvala ti puno, napokon sam ga uspjela do kraja i točan je.  (dođe mi da plačem od sreće što sam ga napokon dovršila hahaha) (dođe mi da plačem od sreće što sam ga napokon dovršila hahaha)
Još uvijek mi ovo objašnjenje treba ako netko zna:
I iz ove skriptice 2.35. a) i b): http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_3.pdf
2.35. a) ne znam kako bi, a 2.35. b) sam došla do jednog dijela pa sam zapela.. Podijelila sam polinome i ono što sam mogla sam integrirala.
[dtex]\frac{x^2}{2}+x+\int \frac{4x^3+4x^2-4x-6}{(x^2-2)^2}dx[/dtex]
I sad sam ovaj integral razdvojila ovako:
[dtex]4\int\frac{x^3}{(x^2-2)^2}dx+4\int\frac{x^2}{(x^2-2)^2}dx-4\int\frac{x}{(x^2-2)^2}dx-6\int\frac{1}{(x^2-2)^2}dx[/dtex]
Drugi i treći integral sam sredila i provjerila s wolfram alphom. No prvi i četvrti me muče. Četvrti ne znam kako bih, a prvi mi se u jednoj stvari razlikuje sa wolframom alphom pa mi recite di sam fulala..
[dtex]4\int\frac{x^3}{(x^2-2)^2}dx= [u=x^2, du=2xdx, dv=\frac{xdx}{(x^2-2)^2}, v=\frac{-1}{2(x^2-2)}] =\frac{-2x^2}{x^2-2}+4\int\frac{xdx}{x^2-2} = \frac{-2x^2}{x^2-2}+4\int\frac{\frac{dt}{2}}{t} = \frac{-2x^2}{x^2-2}+2ln(x^2-2)[/dtex]
I sad wolfram alpha logaritam dobije isto, ali ovo ispred dobije: [dtex]\frac{-4}{x^2-2}[/dtex]
Di je greška? 
2.34. a) imam.
Prvo na parcijalne razlomke razdvojiš, zatim napraviš supstituciju t=arctgx, pa tangense raspišeš kao sin/cos, pa ćeš dobiti cos^2, to napišeš kao [tex]\frac{1+cos2t}{2}[/tex] i cos^4, to napišeš kao [tex]\frac{1}{8}(cos4t+4cos2t+3)[/tex] i onda svaki posebno razdvojiš i integriraš i vratiš nazad iz t u x.
Ako treba neki dio raspisat skroz ili provjerit, reci (sad mi je prekasno bilo da i to sve raspisujem  ). ).
|
|
| [Vrh] |
|
Ljubičica
Forumaš(ica)
Pridružen/a: 30. 11. 2012. (19:46:00)
Postovi: (6)16
|
|
| [Vrh] |
|
markann
Forumaš(ica)
Pridružen/a: 07. 10. 2013. (01:37:06)
Postovi: (1F)16
|
 Postano: 20:22 sub, 7. 6. 2014 Naslov: Postano: 20:22 sub, 7. 6. 2014 Naslov: |
    |
|
|
Zad 2.62 ima greske neke, nezz sta je snjim, uglavnom nemoj ga rjesavat hahaha
Za ovaj integral neznam kak bi rjesio pomocu tvog nacina, ali ja bi se drzo "sablone" i samo rastavljo na parcijalne
[dtex] \frac{1}{(x^2-2)^2} = \frac{1}{(x-\sqrt{2})^2(x+\sqrt{2})^2}[/dtex]
[quote="Ljubičica"]Zar u 2.19.d) u nazivniku nije ta zagrada na 3/2 (a ne na 1/2) i onda dobijemo integral od [latex]sint*cost^2*e^t[/latex] ? :))[/quote]
Supstitucija t=arctgx deriviranjem zamjenjuje te 3/2 sa 1/2, tj ostane samo korjen u nazivniku.. Valjda, kolko ja znam xD
Zad 2.62 ima greske neke, nezz sta je snjim, uglavnom nemoj ga rjesavat hahaha
Za ovaj integral neznam kak bi rjesio pomocu tvog nacina, ali ja bi se drzo "sablone" i samo rastavljo na parcijalne
[dtex] \frac{1}{(x^2-2)^2} = \frac{1}{(x-\sqrt{2})^2(x+\sqrt{2})^2}[/dtex]
| Ljubičica (napisa): | Zar u 2.19.d) u nazivniku nije ta zagrada na 3/2 (a ne na 1/2) i onda dobijemo integral od 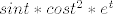 ? ?  ) ) |
Supstitucija t=arctgx deriviranjem zamjenjuje te 3/2 sa 1/2, tj ostane samo korjen u nazivniku.. Valjda, kolko ja znam xD
|
|
| [Vrh] |
|
alenand
Forumaš(ica)

Pridružen/a: 16. 11. 2011. (21:29:52)
Postovi: (18)16
|
 Postano: 22:29 sub, 7. 6. 2014 Naslov: Postano: 22:29 sub, 7. 6. 2014 Naslov: |
    |
|
|
Evo, da i ja bacim koji komentar na sve ovo. Isprike zbog ne praćenja foruma. Uglavnom, valjda sam pohvatao ove teže zadatke:
1. ovo što je kolegica već skoro izračunala do kraja. Samo da primijetim, drugi način je još malo dijelit te polinome - koliko je to već moguće. Konkretno, onaj razlomak pod integralom možemo ovako raspisati:
[dtex]\frac{4x^3+4x^2-4x-6}{(x^2-2)^2}=\frac{4x^3-8x+8x+4x^2-8+8-4x-6}{(x^2-2)^2}=\frac{4x(x^2-2)+4(x^2-2)+4x-2}{(x^2-2)^2}=\frac{4x}{x^2-2}+\frac{4}{x^2-2}+\frac{4x}{(x^2-2)^2}+\frac{2}{(x^2-2)^2}[/dtex]
Iako u suštini nije nešto bolje. Iduće se odnosi kako računati integrale poput zadnjeg:
2. Napisat ću dio izvoda kako reducirati sljedeći integral [dtex]\int \frac{1}{(x^2+a^2)^n}dx[/dtex] za n, u pripadni za n-1. Analogno za slične integrale:
[dtex]I_n=\int \frac{1}{(x^2+a^2)^n}dx=\frac{1}{a^2}\int \frac{a^2}{(x^2+a^2)^n}dx=\frac{1}{a^2}\int\frac{a^2+x^2-x^2}{(x^2+a^2)^n}=\frac{1}{a^2}\int\frac{1}{(x^2+a^2)^{n-1}}dx-\frac{1}{a^2}\int\frac{x^2}{(x^2+a^2)^n}dx=I_{n-1}-\frac{1}{a^2}\int\frac{x^2}{(x^2+a^2)^n}dx[/dtex]
I sad je poanta da je ovaj prvi dio upravo traženi integral za n-1, a drugi dio znamo (donekle) parcijalno integrirati. I tako negdje na desnoj strani se pojavi integral [tex]I_n[/tex] , prebaciš ga na drugu stranu itd. Nadam se da su daljni koraci jasni, ne znam kako ostalima, ali naporno je pisati sve te \frac...
Rezultat bi trebala bit sljedeća redukcijska formula:
[dtex]I_n=\frac{1}{2(n-1)a^2}\left(\frac{x}{(x^2+a^2)^{n-1}}+(2n-3)I_{n-1}\right)[/dtex]
U svakom slučaju, za konkretne integrale postaje bolje, samo treba imati na pamet tako neku ideju.
Za primjer uzmimo 2.34a)
[dtex]\int\frac{x^2}{(x^2+1)^3}dx[/dtex]
Ovo već je pogodno za parcijalnu integraciju poput u općenitom gornjem postupku, pa imamo
[dtex]\int\frac{x^2}{(x^2+1)^3}dx=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\int\frac{1}{(x^2+1)^2}dx[/dtex]
I sad se je stvar svela na računanje integrala sličnog gore, za a=1, n=2. Vidimo da parcijalna integracija funkcionira kad je u brojniku x^2, pa probamo ga odnekud stvorit i vidjet što se događa:
[dtex]=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\int\frac{1+x^2-x^2}{(x^2+1)^2}dx=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\int\frac{1}{(x^2+1)}dx+\frac{-1}{4}\int\frac{x^2}{(1+x^2)^2}dx=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\arctan{x}+\frac{-1}{4}\int\frac{x^2}{(1+x^2)^2}dx[/dtex]
A ovaj zadnji integral opet parcijalnom integracijom itd. Tako bi se slično moglo i onaj [dtex]\frac{1}{(x^2-2)^2}=\frac{1}{2}\frac{2-x^2+x^2}{(x^2-2)}[/dtex] i tako dalje. Nadam se da je jasno, ako ne, molim te pitaj me uživo.
3. Ok, samo kratki postupak za ovaj 2.20b) što ga malo pojednostavljuje. Primijetimo da bi ovo bilo lako da je u brojniku [tex]x^2[/tex]. Ustvari toliko bi nam pojednostavnilo stvar da upravo tu ideju možemo iskoristit u parcijalnoj integraciji:
[dtex]\int\frac{x^3}{(x^3+1)^2}dx=-\frac{1}{3}\frac{x}{1+x^3}+\frac{1}{3}\int\frac{1}{x^3+1}dx[/dtex]
Dalje se ovo svakako mora riješavat parcijalnim razlomcima.
4. U ovom integralu je ideja prvo raspisati sin2x, onda supstituirati t^2=tan x (yup, strpljenje s LaTeX mi je na kraju, sorry :/).
[dtex]\int\frac{\cos x}{\sqrt{\sin2x}}dx=\int\sqrt{\frac{\cos x}{2\sin x}}dx[/dtex]
Stavimo najavljeni t^2=tan x, pa dobivamo:
[dtex]2tdt=\frac{1}{\cos^2x}dx=(1+\tan^2x)dx[/dtex]
No sad, tan x=t^2 => (tan x)^2= t^4 pa napokon:
[dtex]dx=\frac{2t}{1+t^4}dt[/dtex]
Pa integral postaje:
[dtex]\frac{1}{\sqrt{2}}\int \frac{2}{1+t^4}dt[/dtex]
A to je jedan dosadan integral koji je riješen negdje u skripti, mislim u poglavlju s racionalnim funkcijama. Uglavnom, vrlo dosadno rastavljanje na parcijalne razlomke :/
I napokon samo da primijetim, 2.62. je krivo izračunat, ali inače je trivijalan zadatak, a 2.35.a) nije u suštini težak (rastav na parcijalne razlomke), ali je poprilično nemoguć za čovjeka. U svakom slučaju, ne isplati se računati ga ikako osim s wolframom.
Evo, da i ja bacim koji komentar na sve ovo. Isprike zbog ne praćenja foruma. Uglavnom, valjda sam pohvatao ove teže zadatke:
1. ovo što je kolegica već skoro izračunala do kraja. Samo da primijetim, drugi način je još malo dijelit te polinome - koliko je to već moguće. Konkretno, onaj razlomak pod integralom možemo ovako raspisati:
[dtex]\frac{4x^3+4x^2-4x-6}{(x^2-2)^2}=\frac{4x^3-8x+8x+4x^2-8+8-4x-6}{(x^2-2)^2}=\frac{4x(x^2-2)+4(x^2-2)+4x-2}{(x^2-2)^2}=\frac{4x}{x^2-2}+\frac{4}{x^2-2}+\frac{4x}{(x^2-2)^2}+\frac{2}{(x^2-2)^2}[/dtex]
Iako u suštini nije nešto bolje. Iduće se odnosi kako računati integrale poput zadnjeg:
2. Napisat ću dio izvoda kako reducirati sljedeći integral [dtex]\int \frac{1}{(x^2+a^2)^n}dx[/dtex] za n, u pripadni za n-1. Analogno za slične integrale:
[dtex]I_n=\int \frac{1}{(x^2+a^2)^n}dx=\frac{1}{a^2}\int \frac{a^2}{(x^2+a^2)^n}dx=\frac{1}{a^2}\int\frac{a^2+x^2-x^2}{(x^2+a^2)^n}=\frac{1}{a^2}\int\frac{1}{(x^2+a^2)^{n-1}}dx-\frac{1}{a^2}\int\frac{x^2}{(x^2+a^2)^n}dx=I_{n-1}-\frac{1}{a^2}\int\frac{x^2}{(x^2+a^2)^n}dx[/dtex]
I sad je poanta da je ovaj prvi dio upravo traženi integral za n-1, a drugi dio znamo (donekle) parcijalno integrirati. I tako negdje na desnoj strani se pojavi integral [tex]I_n[/tex] , prebaciš ga na drugu stranu itd. Nadam se da su daljni koraci jasni, ne znam kako ostalima, ali naporno je pisati sve te \frac...
Rezultat bi trebala bit sljedeća redukcijska formula:
[dtex]I_n=\frac{1}{2(n-1)a^2}\left(\frac{x}{(x^2+a^2)^{n-1}}+(2n-3)I_{n-1}\right)[/dtex]
U svakom slučaju, za konkretne integrale postaje bolje, samo treba imati na pamet tako neku ideju.
Za primjer uzmimo 2.34a)
[dtex]\int\frac{x^2}{(x^2+1)^3}dx[/dtex]
Ovo već je pogodno za parcijalnu integraciju poput u općenitom gornjem postupku, pa imamo
[dtex]\int\frac{x^2}{(x^2+1)^3}dx=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\int\frac{1}{(x^2+1)^2}dx[/dtex]
I sad se je stvar svela na računanje integrala sličnog gore, za a=1, n=2. Vidimo da parcijalna integracija funkcionira kad je u brojniku x^2, pa probamo ga odnekud stvorit i vidjet što se događa:
[dtex]=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\int\frac{1+x^2-x^2}{(x^2+1)^2}dx=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\int\frac{1}{(x^2+1)}dx+\frac{-1}{4}\int\frac{x^2}{(1+x^2)^2}dx=\frac{-1}{4}\frac{x}{(x^2+1)^2}+\frac{1}{4}\arctan{x}+\frac{-1}{4}\int\frac{x^2}{(1+x^2)^2}dx[/dtex]
A ovaj zadnji integral opet parcijalnom integracijom itd. Tako bi se slično moglo i onaj [dtex]\frac{1}{(x^2-2)^2}=\frac{1}{2}\frac{2-x^2+x^2}{(x^2-2)}[/dtex] i tako dalje. Nadam se da je jasno, ako ne, molim te pitaj me uživo.
3. Ok, samo kratki postupak za ovaj 2.20b) što ga malo pojednostavljuje. Primijetimo da bi ovo bilo lako da je u brojniku [tex]x^2[/tex]. Ustvari toliko bi nam pojednostavnilo stvar da upravo tu ideju možemo iskoristit u parcijalnoj integraciji:
[dtex]\int\frac{x^3}{(x^3+1)^2}dx=-\frac{1}{3}\frac{x}{1+x^3}+\frac{1}{3}\int\frac{1}{x^3+1}dx[/dtex]
Dalje se ovo svakako mora riješavat parcijalnim razlomcima.
4. U ovom integralu je ideja prvo raspisati sin2x, onda supstituirati t^2=tan x (yup, strpljenje s LaTeX mi je na kraju, sorry  ). ).
[dtex]\int\frac{\cos x}{\sqrt{\sin2x}}dx=\int\sqrt{\frac{\cos x}{2\sin x}}dx[/dtex]
Stavimo najavljeni t^2=tan x, pa dobivamo:
[dtex]2tdt=\frac{1}{\cos^2x}dx=(1+\tan^2x)dx[/dtex]
No sad, tan x=t^2 ⇒ (tan x)^2= t^4 pa napokon:
[dtex]dx=\frac{2t}{1+t^4}dt[/dtex]
Pa integral postaje:
[dtex]\frac{1}{\sqrt{2}}\int \frac{2}{1+t^4}dt[/dtex]
A to je jedan dosadan integral koji je riješen negdje u skripti, mislim u poglavlju s racionalnim funkcijama. Uglavnom, vrlo dosadno rastavljanje na parcijalne razlomke 
I napokon samo da primijetim, 2.62. je krivo izračunat, ali inače je trivijalan zadatak, a 2.35.a) nije u suštini težak (rastav na parcijalne razlomke), ali je poprilično nemoguć za čovjeka. U svakom slučaju, ne isplati se računati ga ikako osim s wolframom.
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
 Postano: 1:35 ned, 8. 6. 2014 Naslov: Postano: 1:35 ned, 8. 6. 2014 Naslov: |
    |
|
|
Hvala na prijedlogu markann, ali bilo mi je bolje po alenandovom, sad ću ubuduće znat sređivat ovakve integrale. Stvarno hvala puno alenand na raspisivanju (i meni je naporno pisat sve to u latexu, sve pet :) ). Uspjela sam ga dobit isto kao wolfram alpha. :D
I hvala za 2.45. c), ne da mi se dalje to sređivat jer je neki dugačak raspis, ali bitan mi je bio početak.
I prihvatit ću savjet da preskočim 2.35 a) jer je dosadan i da je 2.62. krivi. :wink:
Sutra/preksutra se javim s novim zadacima koji mi neće bit jasni, moram još neke opet probat ili provjerit, da ne odustanem odmah. :D
[quote="Ljubičica"]Zar u 2.19.d) u nazivniku nije ta zagrada na 3/2 (a ne na 1/2) i onda dobijemo integral od [latex]sint*cost^2*e^t[/latex] ? :))[/quote]
[dtex]\int \frac{xe^{arctgx}}{(1-x^2)(1+x^2)^{\frac{1}{2}}}dx [/dtex]
Supstitucija: [dtex] [t=arctgx, x=tgt, dt=\frac{1}{1+x^2}dx ]= \int \frac{tgte^t}{(tg^2t+1)^\frac{1}{2}}dt [/dtex]
Hvala na prijedlogu markann, ali bilo mi je bolje po alenandovom, sad ću ubuduće znat sređivat ovakve integrale. Stvarno hvala puno alenand na raspisivanju (i meni je naporno pisat sve to u latexu, sve pet  ). Uspjela sam ga dobit isto kao wolfram alpha. ). Uspjela sam ga dobit isto kao wolfram alpha. 
I hvala za 2.45. c), ne da mi se dalje to sređivat jer je neki dugačak raspis, ali bitan mi je bio početak.
I prihvatit ću savjet da preskočim 2.35 a) jer je dosadan i da je 2.62. krivi. 
Sutra/preksutra se javim s novim zadacima koji mi neće bit jasni, moram još neke opet probat ili provjerit, da ne odustanem odmah. 
| Ljubičica (napisa): | Zar u 2.19.d) u nazivniku nije ta zagrada na 3/2 (a ne na 1/2) i onda dobijemo integral od 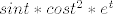 ? ?  ) ) |
[dtex]\int \frac{xe^{arctgx}}{(1-x^2)(1+x^2)^{\frac{1}{2}}}dx [/dtex]
Supstitucija: [dtex] [t=arctgx, x=tgt, dt=\frac{1}{1+x^2}dx ]= \int \frac{tgte^t}{(tg^2t+1)^\frac{1}{2}}dt [/dtex]
|
|
| [Vrh] |
|
Ljubičica
Forumaš(ica)
Pridružen/a: 30. 11. 2012. (19:46:00)
Postovi: (6)16
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
hendrix
Forumaš(ica)

Pridružen/a: 03. 09. 2012. (15:59:06)
Postovi: (92)16
|
|
| [Vrh] |
|
relax
Forumaš(ica)

Pridružen/a: 01. 02. 2014. (20:23:33)
Postovi: (1E)16
Spol: 
|
 Postano: 20:07 sub, 14. 6. 2014 Naslov: Postano: 20:07 sub, 14. 6. 2014 Naslov: |
    |
|
|
Nije u vezi integrala, ali je gradivo za drugi kol:
ako imamo red tipa
[dtex]\Sigma n!x^{n!}[/dtex] i racunamo radijus konvergencije, mozemo li supstituirati [tex]t = n! [/tex] pa dalje provjeravati (D'Alembert):
[dtex]R = lim_{t \to \infty} \frac{a_{n}}{a_{n+1}} = \frac{t}{t+1} = 1[/dtex]
Ako provjeravam
[dtex]R = lim_{n \to \infty} \frac{n!}{(n+1)!} = \frac{1}{n+1} = 0[/dtex], a to nije ispravno rjesenje
Je li onda ispravno ono prvo? Moze li se to opcenito koristiti kada je potencija od [tex](x-c) [/tex]razlicita od [tex]n[/tex], kao u ovom slucaju [tex]n![/tex] ?
EDIT: ispravljeno iz [tex]\infty[/tex] u [tex]0[/tex], moj previd :D
Nije u vezi integrala, ali je gradivo za drugi kol:
ako imamo red tipa
[dtex]\Sigma n!x^{n!}[/dtex] i racunamo radijus konvergencije, mozemo li supstituirati [tex]t = n! [/tex] pa dalje provjeravati (D'Alembert):
[dtex]R = lim_{t \to \infty} \frac{a_{n}}{a_{n+1}} = \frac{t}{t+1} = 1[/dtex]
Ako provjeravam
[dtex]R = lim_{n \to \infty} \frac{n!}{(n+1)!} = \frac{1}{n+1} = 0[/dtex], a to nije ispravno rjesenje
Je li onda ispravno ono prvo? Moze li se to opcenito koristiti kada je potencija od [tex](x-c) [/tex]razlicita od [tex]n[/tex], kao u ovom slucaju [tex]n![/tex] ?
EDIT: ispravljeno iz [tex]\infty[/tex] u [tex]0[/tex], moj previd 
Zadnja promjena: relax; 22:27 sub, 14. 6. 2014; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
 Postano: 23:49 sub, 14. 6. 2014 Naslov: Postano: 23:49 sub, 14. 6. 2014 Naslov: |
    |
|
|
[quote="room"]
Zna li netko iz nepravih integrala 2.59. b)[/quote]
Imaš na forumu hint, potraži "2.59" u tražilici.
Ako se dobro sjećam, poanta je izmnožiti (x-a)(b-x) pa dobiveni izraz izraziti ovako [tex]M^2 - (x-N)^2[/tex] gdje su M i N neki izrazi uz pomoć a i b pa imaš.
[dtex]\int \frac{\,dx}{\sqrt{M^2 - (x-N)^2}} = \frac{1}{M}\arcsin\frac{x-N}{M}[/dtex]
[quote="room"] i 2.60. a i d? [url]http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_6.pdf[/url][/quote]
a) Ja sam to ovako (valjda je dobro):
[dtex]\sin x < x \implies \sqrt{\sin x} < \sqrt{x} \implies \frac{1}{\sqrt{\sin x}} > \frac{1}{\sqrt{x}} > \frac{1}{x}[/dtex]
(nalazimo se na intervalu 0 do pi/2 i imamo funkciju oblika [dtex]\frac{1}{x^p}[/dtex] za p=1 pa divergira)
d)
Sve f-je na tom intervalu su veće ili jednake 0 i:
[dtex]ln(1+x) < x \\
\tan x = \frac{\sin x}{\cos x} < \frac{x}{\cos x} \leq \frac{x}{1}[/dtex]
na kraju kad pokratiš sve imaš: [dtex]\frac{1}{x^{1/2}}[/dtex] , 0 < p = 1/2 < 1 pa konvergira.
Moguće da imam negdje grešku, kasno je -.-
EDIT za d), sad kad gledam intervale, vidim da bi trebalo biti:
[dtex]\tan x = \frac{\sin x}{\cos x} < \frac{x}{\cos x} \leq \frac{x}{\cos 1}[/dtex]
pa kad se sve pokrati bi trebalo biti:
[dtex]\int_0^1 \frac{\,dx}{\cos 1 x^{1/2}}[/dtex]
no sad se valjda [tex]\frac{1}{\cos 1}[/tex] izluči ispred integrala pa opet imamo konvergenciju (čini mi se).
| room (napisa): |
Zna li netko iz nepravih integrala 2.59. b) |
Imaš na forumu hint, potraži "2.59" u tražilici.
Ako se dobro sjećam, poanta je izmnožiti (x-a)(b-x) pa dobiveni izraz izraziti ovako [tex]M^2 - (x-N)^2[/tex] gdje su M i N neki izrazi uz pomoć a i b pa imaš.
[dtex]\int \frac{\,dx}{\sqrt{M^2 - (x-N)^2}} = \frac{1}{M}\arcsin\frac{x-N}{M}[/dtex]
a) Ja sam to ovako (valjda je dobro):
[dtex]\sin x < x \implies \sqrt{\sin x} < \sqrt{x} \implies \frac{1}{\sqrt{\sin x}} > \frac{1}{\sqrt{x}} > \frac{1}{x}[/dtex]
(nalazimo se na intervalu 0 do pi/2 i imamo funkciju oblika [dtex]\frac{1}{x^p}[/dtex] za p=1 pa divergira)
d)
Sve f-je na tom intervalu su veće ili jednake 0 i:
[dtex]ln(1+x) < x \\
\tan x = \frac{\sin x}{\cos x} < \frac{x}{\cos x} \leq \frac{x}{1}[/dtex]
na kraju kad pokratiš sve imaš: [dtex]\frac{1}{x^{1/2}}[/dtex] , 0 < p = 1/2 < 1 pa konvergira.
Moguće da imam negdje grešku, kasno je -.-
EDIT za d), sad kad gledam intervale, vidim da bi trebalo biti:
[dtex]\tan x = \frac{\sin x}{\cos x} < \frac{x}{\cos x} \leq \frac{x}{\cos 1}[/dtex]
pa kad se sve pokrati bi trebalo biti:
[dtex]\int_0^1 \frac{\,dx}{\cos 1 x^{1/2}}[/dtex]
no sad se valjda [tex]\frac{1}{\cos 1}[/tex] izluči ispred integrala pa opet imamo konvergenciju (čini mi se).
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
|















