| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gia
Forumaš(ica)

Pridružen/a: 20. 06. 2004. (00:46:02)
Postovi: (1D)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 0:58 uto, 21. 9. 2004 Naslov: Re: problem sa jednim zad... Postano: 0:58 uto, 21. 9. 2004 Naslov: Re: problem sa jednim zad... |
    |
|
|
[quote="Gia"]imam jedan zad pa ako netko zna neka ga rijesi..
Neka je f fja klase C1 sa R2 u R. Dokazite da postoji neprekidna injekcija g sa [0,1] u R2 td je f°g konstanta.
:?:[/quote]
prevario se, nastavit cu raditi ujutro, ako netko moze obrisat ovi post ili cu ga ja prepravit kada/ako bude vremena za to?
| Gia (napisa): | imam jedan zad pa ako netko zna neka ga rijesi..
Neka je f fja klase C1 sa R2 u R. Dokazite da postoji neprekidna injekcija g sa [0,1] u R2 td je f°g konstanta.
 |
prevario se, nastavit cu raditi ujutro, ako netko moze obrisat ovi post ili cu ga ja prepravit kada/ako bude vremena za to?
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
defar
Forumaš(ica)


Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
 Postano: 15:15 uto, 21. 9. 2004 Naslov: Postano: 15:15 uto, 21. 9. 2004 Naslov: |
    |
|
|
hm...a sto si ti zubich vilo pisajO?.....ako je fja f konstantna, moze se uzet za g bilo kakav regularan gladak put, oukej.
ako nije, treba derivacija od g u svakoj tocki iz (0,1) bit ortogonalna diferencijalu od f(g(t))....(treba postojat neki put koji se probija kroz graf fje f tako da f(g(t)) ostaje na istom nivou)-jel to u redu reci?
mislim, ako je fog konstanta, onda je (fog)' 0 u svakoj tocki, tj. f'(g(t))*g'(t)=0, to je nuzno.
ne i dovoljno...al fja je klase C1....sto to govori o diferencijalu od f? osim da postoji?
a fja f je glatka. a put ne bi smio biti konst. na nijednom svom dijelu, da bi bijo injektivan, tj derivacija mu mora bit razlicita od 0, dobro.
derivacija puta...to po jednoj, pa po drugoj var nezavisno (meni se strasno spava)..
onda, ljudi, sto znamo o ortogonalnim vektorima? jel to dovoljno?
jel se moze nekako dobit vec sad kakvog oblika treba bit g'(t) da bi bio ortogonalan s Df(g(t)), pa onda integrirat po prvoj, pa po drugoj, i propisat put g tako nekako preko f?
hm...a sto si ti zubich vilo pisajO?.....ako je fja f konstantna, moze se uzet za g bilo kakav regularan gladak put, oukej.
ako nije, treba derivacija od g u svakoj tocki iz (0,1) bit ortogonalna diferencijalu od f(g(t))....(treba postojat neki put koji se probija kroz graf fje f tako da f(g(t)) ostaje na istom nivou)-jel to u redu reci?
mislim, ako je fog konstanta, onda je (fog)' 0 u svakoj tocki, tj. f'(g(t))*g'(t)=0, to je nuzno.
ne i dovoljno...al fja je klase C1....sto to govori o diferencijalu od f? osim da postoji?
a fja f je glatka. a put ne bi smio biti konst. na nijednom svom dijelu, da bi bijo injektivan, tj derivacija mu mora bit razlicita od 0, dobro.
derivacija puta...to po jednoj, pa po drugoj var nezavisno (meni se strasno spava)..
onda, ljudi, sto znamo o ortogonalnim vektorima? jel to dovoljno?
jel se moze nekako dobit vec sad kakvog oblika treba bit g'(t) da bi bio ortogonalan s Df(g(t)), pa onda integrirat po prvoj, pa po drugoj, i propisat put g tako nekako preko f?
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 23:50 uto, 21. 9. 2004 Naslov: Postano: 23:50 uto, 21. 9. 2004 Naslov: |
    |
|
|
[quote="defar"]hm...a sto si ti zubich vilo pisajO?.....ako je fja f konstantna, moze se uzet za g bilo kakav regularan gladak put, oukej.
ako nije, treba derivacija od g u svakoj tocki iz (0,1) bit ortogonalna diferencijalu od f(g(t))....(treba postojat neki put koji se probija kroz graf fje f tako da f(g(t)) ostaje na istom nivou)-jel to u redu reci?
mislim, ako je fog konstanta, onda je (fog)' 0 u svakoj tocki, tj. f'(g(t))*g'(t)=0, to je nuzno.
ne i dovoljno...[/quote]
Jest i dovoljno. Ako je domena povezana, a jest. :-)
[quote]al fja je klase C1....sto to govori o diferencijalu od f? osim da postoji?[/quote]
Da je neprekidan? :-)
[quote]derivacija puta...to po jednoj, pa po drugoj var nezavisno[/quote]
Odnosno, gornje množenje ti je skalarni produkt dva 2-vektora.
[quote] (meni se strasno spava)..[/quote]
Nisi jedina... :needsleep:
[quote]jel se moze nekako dobit vec sad kakvog oblika treba bit g'(t) da bi bio ortogonalan s Df(g(t)), pa onda integrirat po prvoj, pa po drugoj, i propisat put g tako nekako preko f?[/quote]
Vjerojatno može. Ako je jutro. A nije. Još. :-/
| defar (napisa): | hm...a sto si ti zubich vilo pisajO?.....ako je fja f konstantna, moze se uzet za g bilo kakav regularan gladak put, oukej.
ako nije, treba derivacija od g u svakoj tocki iz (0,1) bit ortogonalna diferencijalu od f(g(t))....(treba postojat neki put koji se probija kroz graf fje f tako da f(g(t)) ostaje na istom nivou)-jel to u redu reci?
mislim, ako je fog konstanta, onda je (fog)' 0 u svakoj tocki, tj. f'(g(t))*g'(t)=0, to je nuzno.
ne i dovoljno... |
Jest i dovoljno. Ako je domena povezana, a jest. 
| Citat: | | al fja je klase C1....sto to govori o diferencijalu od f? osim da postoji? |
Da je neprekidan? 
| Citat: | | derivacija puta...to po jednoj, pa po drugoj var nezavisno |
Odnosno, gornje množenje ti je skalarni produkt dva 2-vektora.
| Citat: | | (meni se strasno spava).. |
Nisi jedina... 
| Citat: | | jel se moze nekako dobit vec sad kakvog oblika treba bit g'(t) da bi bio ortogonalan s Df(g(t)), pa onda integrirat po prvoj, pa po drugoj, i propisat put g tako nekako preko f? |
Vjerojatno može. Ako je jutro. A nije. Još. :-/
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 0:00 sri, 22. 9. 2004 Naslov: Postano: 0:00 sri, 22. 9. 2004 Naslov: |
    |
|
|
[quote="defar"]jel se moze nekako dobit vec sad kakvog oblika treba bit g'(t) da bi bio ortogonalan s Df(g(t)), pa onda integrirat po prvoj, pa po drugoj, i propisat put g tako nekako preko f?[/quote]
Mitlin da nece ici, jerbo nemas dobro definiranu primitivnu fju unutar toga kolegija da bi to ucinila?
iako da.. intuitivna interpretacija ovog problema bi bila "da li postoji put u R2 t.d. je proizvoljna fja klase C1 na njemu konstantna" :) vizualizacija? zemljopisne karte? (izohipse, probaj zamisliti "svijet" u R2 u kojem ih ne mozemo "napraviti" :shock:)
(utoliko bi dokaz preko gradijenta fje bio mnogo "opisniji" od onog kojeg cu sprovesti :?)
Dakle, teorem o impl. fji :D, definiramo:
[latex]\displaystyle
F(x,y;c)=f(x,y)-c \Rightarrow \partial_y F(x,y;c)=\partial_y f(x,y)[/latex]
Dakle, imamo dva slucaja, prvi:
[latex]\displaystyle
\partial_y F(x_0,y_0;c)=0 ~ ~ \forall (x_0,y_0) \Rightarrow ~def. ~\overline f_{x_0}:=f \vert_{\{(x_0, y) : y \in R \}} \Rightarrow[/latex]
[latex]\displaystyle
\overline {f`}_{x_0}(y)=0 ~ ~\forall y \Rightarrow \overline f_{x_0} $ jest konstantna $ \forall x_0 \Rightarrow \\ \Rightarrow g_{x_0}(y):=(x_0,y) : [0,1] \rightarrow R^2 $ jest t.d. $ (f \circ g_{x_0}) $ jest konstantna $\forall x_0[/latex]
Drugi:
[latex]\displaystyle
\exists (x_0,y_0) $ t.d. $ \partial_y F(x_0,y_0;c) \neq 0 \Rightarrow \exists c_0 $ t.d. $ F(x_0,y_0;c_0)=0 \Rightarrow[/latex]
po tm.u o implicitno zadanoj fji:
[latex]\displaystyle
\exists$otvoreni interval $I \subseteq R$ t.d. $\exists \varphi : I \rightarrow R $ t.d. $ F(x, \varphi(x); c_0)=0 ~ ~ \forall x \in I \Rightarrow \\
$specijalno: $\exists h>0 $ t.d. $ [x_0-h/2, x_0+h/2] \subseteq I \Rightarrow\\ g(t):=(x_0-h/2+ t \cdot h, \varphi(x_0-h/2+ t \cdot h)) : [0,1] \rightarrow R^2 $ jest t.d. $ (F \circ g)=0 \\$ t.j. $ f(g(t))=c_0 ~ ~\forall t \in [0,1][/latex]
(btw: presutih da je phi(x) klase C1, te da je, dakle, i g klase C1, pa i neprekidna, analogna opaska i za prvi slucaj, dodatno, bi mozda trebalo napomenuti da je graf fje uvijek injektivan (dokaz za dz :g:), pa je stoga i (x,phi(x)) injektivna fja od x)
Jeto :D
simpaticno :) ovo bi se moglo zvati "propozicijom o [i]izohipsnosti[/i] fja definiranih na ravnini" :D
| defar (napisa): | | jel se moze nekako dobit vec sad kakvog oblika treba bit g'(t) da bi bio ortogonalan s Df(g(t)), pa onda integrirat po prvoj, pa po drugoj, i propisat put g tako nekako preko f? |
Mitlin da nece ici, jerbo nemas dobro definiranu primitivnu fju unutar toga kolegija da bi to ucinila?
iako da.. intuitivna interpretacija ovog problema bi bila "da li postoji put u R2 t.d. je proizvoljna fja klase C1 na njemu konstantna"  vizualizacija? zemljopisne karte? (izohipse, probaj zamisliti "svijet" u R2 u kojem ih ne mozemo "napraviti" vizualizacija? zemljopisne karte? (izohipse, probaj zamisliti "svijet" u R2 u kojem ih ne mozemo "napraviti"  ) )
(utoliko bi dokaz preko gradijenta fje bio mnogo "opisniji" od onog kojeg cu sprovesti  ) )
Dakle, teorem o impl. fji  , definiramo: , definiramo:
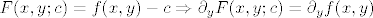
Dakle, imamo dva slucaja, prvi:
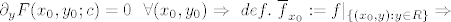

Drugi:
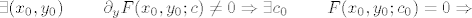
po tm.u o implicitno zadanoj fji:
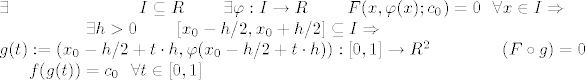
(btw: presutih da je phi(x) klase C1, te da je, dakle, i g klase C1, pa i neprekidna, analogna opaska i za prvi slucaj, dodatno, bi mozda trebalo napomenuti da je graf fje uvijek injektivan (dokaz za dz  ), pa je stoga i (x,phi(x)) injektivna fja od x) ), pa je stoga i (x,phi(x)) injektivna fja od x)
Jeto 
simpaticno  ovo bi se moglo zvati "propozicijom o izohipsnosti fja definiranih na ravnini" ovo bi se moglo zvati "propozicijom o izohipsnosti fja definiranih na ravnini" 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
defar
Forumaš(ica)


Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
 Postano: 10:00 sri, 22. 9. 2004 Naslov: Postano: 10:00 sri, 22. 9. 2004 Naslov: |
    |
|
|
ah, forumasi! :D
lavovi spavaju 15-20 sati dnevno. jer imaju slozenije mozgove/vise vremena(sto nije sasvim nezavisno) od zebre. one spavaju samo malo, i to stojecki.
bavo zubich!(iako mi se trenutno ne da bas jako pazljivo procitat) to je moj prijatelj! :D
a sto se vizualizacije tice - pa i rekla sam izohipse! trag puta na grafu funkcije, na istom nivou. ah, da, al izohipse su zatvorene, jel. mislim, taj moj put moze bit i dio izohipse. :D
ah, forumasi! 
lavovi spavaju 15-20 sati dnevno. jer imaju slozenije mozgove/vise vremena(sto nije sasvim nezavisno) od zebre. one spavaju samo malo, i to stojecki.
bavo zubich!(iako mi se trenutno ne da bas jako pazljivo procitat) to je moj prijatelj! 
a sto se vizualizacije tice - pa i rekla sam izohipse! trag puta na grafu funkcije, na istom nivou. ah, da, al izohipse su zatvorene, jel. mislim, taj moj put moze bit i dio izohipse. 
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 10:13 sri, 22. 9. 2004 Naslov: Postano: 10:13 sri, 22. 9. 2004 Naslov: |
    |
|
|
[quote="defar"]a sto se vizualizacije tice - pa i rekla sam izohipse! trag puta na grafu funkcije, na istom nivou. ah, da, al izohipse su zatvorene, jel. mislim, taj moj put moze bit i dio izohipse. :D[/quote]
Ni izohipse nisu zatvorene ako se protezu "preko ruba" karte ;)
:OT:
[quote="defar"]bavo zubich!(iako mi se trenutno ne da bas jako pazljivo procitat) to je moj prijatelj! :D[/quote]
:o A NA KAVU NE BI ZVALA ? :D
| defar (napisa): | a sto se vizualizacije tice - pa i rekla sam izohipse! trag puta na grafu funkcije, na istom nivou. ah, da, al izohipse su zatvorene, jel. mislim, taj moj put moze bit i dio izohipse.  |
Ni izohipse nisu zatvorene ako se protezu "preko ruba" karte 

| defar (napisa): | bavo zubich!(iako mi se trenutno ne da bas jako pazljivo procitat) to je moj prijatelj!  |
 A NA KAVU NE BI ZVALA ? A NA KAVU NE BI ZVALA ? 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
|




