|
Pa, u principu, bojim se da ne možete naći rješenja okupljena na jednom mjestu. :( Zamišljeno je da za svaki zadatak možete doći odgovarajućem asistentu u vrijeme koje će biti oglašeno na rezultatima i tamo pogledati svoju zadaću/ispravno rješenje zadatka.
Ja mogu napisati rješenja (samo rezultate) za zadatak koji sam ja zadao. Postoje četiri grupe zadataka, možda su malo izmiješane:
2.(a)
f(x)=x^2+2x-3
f(<-2,1>)=[-4,0>
[latex]f^{-1}[/latex](<-oo,5])=[-4,2]
f(x)=-x^2-4x
f([-4,0>)=[0,4]
[latex]f^{-1}[/latex]([0,3>)=[-4,-3>U<-1,0]
f(x)=x^2+6x+8
f(<-5,0])=[-1,8]
[latex]f^{-1}[/latex](<-2,0>)=<-4,-2>
f(x)=-x^2+4x-3
f(<-1,3>)=<-8,1]
[latex]f^{-1}[/latex](<-oo,-3>)=<-oo,0>U<4,+oo>
2.(b)
f(x)=||2^x-2|-3|
f(<-oo,2>)=<1,3]
[latex]f^{-1}[/latex](<0,3])=<-oo,[latex]\log_{2}5[/latex]>U<[latex]\log_{2}5[/latex],3]
f(x)=[latex]\log_{3}(|x+1|+3)[/latex]
f(<-oo,0>)=[1,+oo>
[latex]f^{-1}[/latex](<1,2])=[-7,-1>U<-1,5]
f(x)=|(x+1)^4-1|
f([-2,0>)=[0,1]
[latex]f^{-1}[/latex](<0,3>)=<-[latex]\sqrt{2}[/latex]-1,-2>U<-2,0>U<0,[latex]\sqrt{2}[/latex]-1>
f(x)=[latex]\sqrt[6]{||x-3|-3|}[/latex]
f([-1,2>)=[0,[latex]\sqrt[6]{2}[/latex]>
[latex]f^{-1}[/latex](<-oo,[latex]\sqrt[6]{3}[/latex]>)=<-3,3>U<3,9>
Pa, u principu, bojim se da ne možete naći rješenja okupljena na jednom mjestu.  Zamišljeno je da za svaki zadatak možete doći odgovarajućem asistentu u vrijeme koje će biti oglašeno na rezultatima i tamo pogledati svoju zadaću/ispravno rješenje zadatka. Zamišljeno je da za svaki zadatak možete doći odgovarajućem asistentu u vrijeme koje će biti oglašeno na rezultatima i tamo pogledati svoju zadaću/ispravno rješenje zadatka.
Ja mogu napisati rješenja (samo rezultate) za zadatak koji sam ja zadao. Postoje četiri grupe zadataka, možda su malo izmiješane:
2.(a)
f(x)=x^2+2x-3
f(←2,1>)=[-4,0>
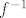 (←oo,5])=[-4,2] (←oo,5])=[-4,2]
f(x)=-x^2-4x
f([-4,0>)=[0,4]
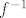 ([0,3>)=[-4,-3>U←1,0] ([0,3>)=[-4,-3>U←1,0]
f(x)=x^2+6x+8
f(←5,0])=[-1,8]
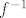 (←2,0>)=←4,-2> (←2,0>)=←4,-2>
f(x)=-x^2+4x-3
f(←1,3>)=←8,1]
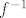 (←oo,-3>)=←oo,0>U<4,+oo> (←oo,-3>)=←oo,0>U<4,+oo>
2.(b)
f(x)=||2^x-2|-3|
f(←oo,2>)=<1,3]
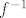 (<0,3])=←oo, (<0,3])=←oo,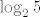 >U< >U<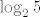 ,3] ,3]
f(x)=
f(←oo,0>)=[1,+oo>
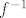 (<1,2])=[-7,-1>U←1,5] (<1,2])=[-7,-1>U←1,5]
f(x)=|(x+1)^4-1|
f([-2,0>)=[0,1]
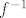 (<0,3>)=← (<0,3>)=←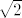 -1,-2>U←2,0>U<0, -1,-2>U←2,0>U<0,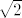 -1> -1>
f(x)=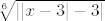
f([-1,2>)=[0,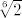 > >
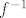 (←oo, (←oo,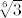 >)=←3,3>U<3,9> >)=←3,3>U<3,9>
|








