| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 16:02 čet, 17. 2. 2005 Naslov: dopuna do ortogonalne baze Postano: 16:02 čet, 17. 2. 2005 Naslov: dopuna do ortogonalne baze |
    |
|
|
Dopunite do ortogonalne (obzirom na standardni skalarni produkt) bazu za R4 skup {(1,-2,2,-3), (2,-3,2,4)}
ja sam to ovako rjesio :
1 -2 2 3
2 -3 2 4
prvom sam redak pomnozio sa -2 i dodao drugom, nakon cega sam 2. redak pomnozio sa 2 i dodao prvom i dobio
1 0 -2 7
0 1 -2 10
i onda sam
x=( -2s-7t, -2s+10t, s, t)
(-2,-2,1,0), (-7,10,0,1)
je li sam dobro ovo rijesio?
da li se ovaj zadatak moze rjesiti jos pomocu Gram-Schmidt-ovog postupka ortogonalizacije?
Dopunite do ortogonalne (obzirom na standardni skalarni produkt) bazu za R4 skup {(1,-2,2,-3), (2,-3,2,4)}
ja sam to ovako rjesio :
1 -2 2 3
2 -3 2 4
prvom sam redak pomnozio sa -2 i dodao drugom, nakon cega sam 2. redak pomnozio sa 2 i dodao prvom i dobio
1 0 -2 7
0 1 -2 10
i onda sam
x=( -2s-7t, -2s+10t, s, t)
(-2,-2,1,0), (-7,10,0,1)
je li sam dobro ovo rijesio?
da li se ovaj zadatak moze rjesiti jos pomocu Gram-Schmidt-ovog postupka ortogonalizacije?
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 16:57 čet, 17. 2. 2005 Naslov: Re: dopuna do ortogonalne baze Postano: 16:57 čet, 17. 2. 2005 Naslov: Re: dopuna do ortogonalne baze |
    |
|
|
[quote="filipnet"]
snip
da li se ovaj zadatak moze rjesiti jos pomocu Gram-Schmidt-ovog postupka ortogonalizacije?[/quote]
samo da ti napisem. razlog zato sam pao (again :( ) linearnu 2 na proslom roku jest, izmedju ostaloga, i taj sto sam upotrijebio Gram-Schmidtov postupak za rjesavanje istog zadatka.
Gram-schmidtov postupak provodi se kod ortonormiranja baze linearnog prostora, a ne kod ortogonalizacije.
Ortogonalizacija baze znaci sljedece:
predpostavimo da imamo prostor [latex]R^4[/latex] i [latex]L=[x_1, x_2]\leq R^4[/latex]. da bi dobili [latex]L^\perp[/latex] moramo preko skalarnog produkta (standardnog, aki isti nije definiran u zadatku) naci dva vektora, primjerice [latex]x_3, x_4 \in L^\perp[/latex] koji ce biti okomiti na vektore [latex]x_1, x_2 \in L[/latex].
tada [latex]L \bigoplus L^\perp=R^4[/latex], odnosno, vektori iz [latex]L[/latex] i [latex]L^\perp[/latex] cine bazu pocetnog prostora (u ovom slucaju [latex]R^4[/latex]).
eto...nadam se da sam ti pomogao (barem dijelom). ispricavam se ako ima kakvih tipfelera (mislim da kuzis sta sam htio reci ;-) ).
| filipnet (napisa): |
snip
da li se ovaj zadatak moze rjesiti jos pomocu Gram-Schmidt-ovog postupka ortogonalizacije? |
samo da ti napisem. razlog zato sam pao (again  ) linearnu 2 na proslom roku jest, izmedju ostaloga, i taj sto sam upotrijebio Gram-Schmidtov postupak za rjesavanje istog zadatka. ) linearnu 2 na proslom roku jest, izmedju ostaloga, i taj sto sam upotrijebio Gram-Schmidtov postupak za rjesavanje istog zadatka.
Gram-schmidtov postupak provodi se kod ortonormiranja baze linearnog prostora, a ne kod ortogonalizacije.
Ortogonalizacija baze znaci sljedece:
predpostavimo da imamo prostor 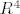 i i 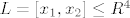 . da bi dobili . da bi dobili 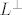 moramo preko skalarnog produkta (standardnog, aki isti nije definiran u zadatku) naci dva vektora, primjerice moramo preko skalarnog produkta (standardnog, aki isti nije definiran u zadatku) naci dva vektora, primjerice 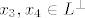 koji ce biti okomiti na vektore koji ce biti okomiti na vektore 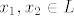 . .
tada 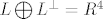 , odnosno, vektori iz , odnosno, vektori iz  i i 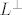 cine bazu pocetnog prostora (u ovom slucaju cine bazu pocetnog prostora (u ovom slucaju 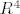 ). ).
eto...nadam se da sam ti pomogao (barem dijelom). ispricavam se ako ima kakvih tipfelera (mislim da kuzis sta sam htio reci  ). ).
|
|
| [Vrh] |
|
Gost
|
 Postano: 21:20 čet, 17. 2. 2005 Naslov: Postano: 21:20 čet, 17. 2. 2005 Naslov: |
    |
|
|
Filipnet, imas pogreske u racunu, to si provjeri, no - da vidimo ono bitno. Zadani vektori su ortogonalni. Dva vektora koji su ortogonalni na njih (a i medjusobno) doista mozemo traziti iz relacija ortogonalnosti (skalarni produkt je 0) sto nam daje dvije homogene jednadzbe s 4 nepoznanice, dakle 2-dim. rjesenje. Onda u tom rjesenju mozemo uzeti bilo koji vektor za treci, a za cetvrti u istom potprostoru L' (to jest ortogonalnom komplementu za potprostor L razapet zadanim vektorima) treba jos postaviti uvjet ortogonalnosti (dobiva se naravno 1-dim. rjesenje). Istina je da radi lakseg racunanja mozemo zadana dva vektora zamijeniti bilo kojom bazom istog potprostora, no operacije koje pritom izvodimo zapravo su iste one koje radimo kod rjesavanja spomenutog sustava jer koordinate vektora su koeficijenti u jednadzbama.
Inace, i Gram-Schmidt se moze primijeniti u tom postupku i sigurno nije to kaznjeno u ispravljanju ispita, nego je valjda bio upotrijebljen na krivi nacin (prva dva vektora se ne diraju u krajnjem rezultatu, normiranje se i ne trazi, ali za treci i cetvrti moze se primijeniti G-S no s tim da se prva dva vektora zamijene ortonormiranom bazom za L).
Filipnet, imas pogreske u racunu, to si provjeri, no - da vidimo ono bitno. Zadani vektori su ortogonalni. Dva vektora koji su ortogonalni na njih (a i medjusobno) doista mozemo traziti iz relacija ortogonalnosti (skalarni produkt je 0) sto nam daje dvije homogene jednadzbe s 4 nepoznanice, dakle 2-dim. rjesenje. Onda u tom rjesenju mozemo uzeti bilo koji vektor za treci, a za cetvrti u istom potprostoru L' (to jest ortogonalnom komplementu za potprostor L razapet zadanim vektorima) treba jos postaviti uvjet ortogonalnosti (dobiva se naravno 1-dim. rjesenje). Istina je da radi lakseg racunanja mozemo zadana dva vektora zamijeniti bilo kojom bazom istog potprostora, no operacije koje pritom izvodimo zapravo su iste one koje radimo kod rjesavanja spomenutog sustava jer koordinate vektora su koeficijenti u jednadzbama.
Inace, i Gram-Schmidt se moze primijeniti u tom postupku i sigurno nije to kaznjeno u ispravljanju ispita, nego je valjda bio upotrijebljen na krivi nacin (prva dva vektora se ne diraju u krajnjem rezultatu, normiranje se i ne trazi, ali za treci i cetvrti moze se primijeniti G-S no s tim da se prva dva vektora zamijene ortonormiranom bazom za L).
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 23:24 čet, 17. 2. 2005 Naslov: Postano: 23:24 čet, 17. 2. 2005 Naslov: |
    |
|
|
hvala! evo ispravka!
(-2,-2,1,0), (17,10,0,1)
hvala! evo ispravka!
(-2,-2,1,0), (17,10,0,1)
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 2:39 pet, 18. 2. 2005 Naslov: Re: dopuna do ortogonalne baze Postano: 2:39 pet, 18. 2. 2005 Naslov: Re: dopuna do ortogonalne baze |
    |
|
|
[quote="HijenA"]samo da ti napisem. razlog zato sam pao (again :( ) linearnu 2 na proslom roku jest, izmedju ostaloga, i taj sto sam upotrijebio Gram-Schmidtov postupak za rjesavanje istog zadatka.
Gram-schmidtov postupak provodi se kod ortonormiranja baze linearnog prostora, a ne kod ortogonalizacije.[/quote]
Za Gram-Schmidtov postupak nije dovoljno da prostor bude linearan, nego i mora imati skalarni produkt. A za takav se prostor veli da je unitaran.
Inače, koliko je meni poznato, ortonormiranje baze je isto kaj i ortogonalizacija, samo kaj se svaki vektor množi sa recipročnom vrijednosti svoje norme, da bi se dobil kolinearni istog smijera duljine 1.
| HijenA (napisa): | samo da ti napisem. razlog zato sam pao (again  ) linearnu 2 na proslom roku jest, izmedju ostaloga, i taj sto sam upotrijebio Gram-Schmidtov postupak za rjesavanje istog zadatka. ) linearnu 2 na proslom roku jest, izmedju ostaloga, i taj sto sam upotrijebio Gram-Schmidtov postupak za rjesavanje istog zadatka.
Gram-schmidtov postupak provodi se kod ortonormiranja baze linearnog prostora, a ne kod ortogonalizacije. |
Za Gram-Schmidtov postupak nije dovoljno da prostor bude linearan, nego i mora imati skalarni produkt. A za takav se prostor veli da je unitaran.
Inače, koliko je meni poznato, ortonormiranje baze je isto kaj i ortogonalizacija, samo kaj se svaki vektor množi sa recipročnom vrijednosti svoje norme, da bi se dobil kolinearni istog smijera duljine 1.
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 15:00 pet, 18. 2. 2005 Naslov: Re: dopuna do ortogonalne baze Postano: 15:00 pet, 18. 2. 2005 Naslov: Re: dopuna do ortogonalne baze |
    |
|
|
[quote="Crni"]
Za Gram-Schmidtov postupak nije dovoljno da prostor bude linearan, nego i mora imati skalarni produkt. A za takav se prostor veli da je unitaran.
Inače, koliko je meni poznato, ortonormiranje baze je isto kaj i ortogonalizacija, samo kaj se svaki vektor množi sa recipročnom vrijednosti svoje norme, da bi se dobil kolinearni istog smijera duljine 1.[/quote]
sad mi objasni zasto sam ja dobio na tom zadatku 0 bodova? proveo sam cijeli Gram-Schmidt, pomnozio vektore reciprocno sa njihovom normom, i dobio 2 vektora koja su se trazila.
| Crni (napisa): |
Za Gram-Schmidtov postupak nije dovoljno da prostor bude linearan, nego i mora imati skalarni produkt. A za takav se prostor veli da je unitaran.
Inače, koliko je meni poznato, ortonormiranje baze je isto kaj i ortogonalizacija, samo kaj se svaki vektor množi sa recipročnom vrijednosti svoje norme, da bi se dobil kolinearni istog smijera duljine 1. |
sad mi objasni zasto sam ja dobio na tom zadatku 0 bodova? proveo sam cijeli Gram-Schmidt, pomnozio vektore reciprocno sa njihovom normom, i dobio 2 vektora koja su se trazila.
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 15:20 pet, 18. 2. 2005 Naslov: Postano: 15:20 pet, 18. 2. 2005 Naslov: |
    |
|
|
nadopunis bazu od M do baze za R4. znaci dodas jos dva vektora npr. (1,0,0,0) i (0,1,0,0) i onda to ortogonaliziras!!
nadopunis bazu od M do baze za R4. znaci dodas jos dva vektora npr. (1,0,0,0) i (0,1,0,0) i onda to ortogonaliziras!!
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 15:23 pet, 18. 2. 2005 Naslov: Postano: 15:23 pet, 18. 2. 2005 Naslov: |
    |
|
|
[quote="filipnet"]nadopunis bazu od M do baze za R4. znaci dodas jos dva vektora npr. (1,0,0,0) i (0,1,0,0) i onda to ortogonaliziras!![/quote]
mislis ortonormiran? sad sam confused :-k
zasto nadopunjivat sa 2 vektora, odnosno sa n-k vektora (ako imamo k vektora, a dimenzija prostora je n)?
pa zar ovo sto smo dobili GM postupkom nije dovoljno da bi bilo baza? sta to nije linearno nezavisan skup vektora koji zajedno sa pocetnim skupom cini bazu vektorskog prostora?
| filipnet (napisa): | | nadopunis bazu od M do baze za R4. znaci dodas jos dva vektora npr. (1,0,0,0) i (0,1,0,0) i onda to ortogonaliziras!! |
mislis ortonormiran? sad sam confused 
zasto nadopunjivat sa 2 vektora, odnosno sa n-k vektora (ako imamo k vektora, a dimenzija prostora je n)?
pa zar ovo sto smo dobili GM postupkom nije dovoljno da bi bilo baza? sta to nije linearno nezavisan skup vektora koji zajedno sa pocetnim skupom cini bazu vektorskog prostora?
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
Gost
|
 Postano: 18:40 pet, 18. 2. 2005 Naslov: Postano: 18:40 pet, 18. 2. 2005 Naslov: |
    |
|
|
Sad, stvarno ne znam zašto su izgubljeni bodovi na pismenom, ali stvar bi u principu trebala biti jasna. Zadani su ortogonalni, ali ne i jedinični vektori a1 i a2. Označimo s e1 i e2 vektore dobivene njihovim normiranjem i dopunimo pomoću dva prikladna vektora a3 i a4 do baze prostora. G-Sch primijenjen na {e1,e2,a3,a4} daje ortonormiranu bazu {e1,e2,e3,e4} pa je {a1,a2,e3,e4} jedno rješenje zadatka. Ovdje je primjena G-Sch čak malo olakšana time što nam je e2 već gotovo "serviran" umjesto da ga izračunavamo "po formuli", pomoću projiciranja na smjer e1. Jasno, {e3,e4} ujedno je i baza ortogonalnog komplementa za potprostor [a1,a2] = [e1,e2].
Pritom, zadatak se lako rješava i bez G-Sch, rješavanjem homogenog sustava 2 jednadžbe s 4 nepoznanice pri čemu se dobiva baza ortogonalnog komplementa, koja se zatim lako zamijeni ortogonalnom bazom, tj. jedan vektor iz rješenja uzmemo po volji, a drugi odredimo tako da je ortogonalan na njega.
Sad, stvarno ne znam zašto su izgubljeni bodovi na pismenom, ali stvar bi u principu trebala biti jasna. Zadani su ortogonalni, ali ne i jedinični vektori a1 i a2. Označimo s e1 i e2 vektore dobivene njihovim normiranjem i dopunimo pomoću dva prikladna vektora a3 i a4 do baze prostora. G-Sch primijenjen na {e1,e2,a3,a4} daje ortonormiranu bazu {e1,e2,e3,e4} pa je {a1,a2,e3,e4} jedno rješenje zadatka. Ovdje je primjena G-Sch čak malo olakšana time što nam je e2 već gotovo "serviran" umjesto da ga izračunavamo "po formuli", pomoću projiciranja na smjer e1. Jasno, {e3,e4} ujedno je i baza ortogonalnog komplementa za potprostor [a1,a2] = [e1,e2].
Pritom, zadatak se lako rješava i bez G-Sch, rješavanjem homogenog sustava 2 jednadžbe s 4 nepoznanice pri čemu se dobiva baza ortogonalnog komplementa, koja se zatim lako zamijeni ortogonalnom bazom, tj. jedan vektor iz rješenja uzmemo po volji, a drugi odredimo tako da je ortogonalan na njega.
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 18:50 pet, 18. 2. 2005 Naslov: Postano: 18:50 pet, 18. 2. 2005 Naslov: |
    |
|
|
[quote="Anonymous"]
Pritom, zadatak se lako rješava i bez G-Sch, rješavanjem homogenog sustava 2 jednadžbe s 4 nepoznanice pri čemu se dobiva baza ortogonalnog komplementa, koja se zatim lako zamijeni ortogonalnom bazom, tj. jedan vektor iz rješenja uzmemo po volji, a drugi odredimo tako da je ortogonalan na njega.[/quote]
pa zar nisam ja tako rjesio zadatak na pocetku posta?
| Anonymous (napisa): |
Pritom, zadatak se lako rješava i bez G-Sch, rješavanjem homogenog sustava 2 jednadžbe s 4 nepoznanice pri čemu se dobiva baza ortogonalnog komplementa, koja se zatim lako zamijeni ortogonalnom bazom, tj. jedan vektor iz rješenja uzmemo po volji, a drugi odredimo tako da je ortogonalan na njega. |
pa zar nisam ja tako rjesio zadatak na pocetku posta?
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|

















