| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
 Postano: 10:51 ned, 17. 4. 2005 Naslov: Postano: 10:51 ned, 17. 4. 2005 Naslov: |
    |
|
|
Zaboravio sam sliku. Dakle, jezgra je jednodimenzionalna, pa je slika (n-1)-dimnzionalna po teoremu o rangu i defektu. Medjutim, ocito u slici moze biti polinom najvise (n-2)-stupnja. Naime, st(D(p))<st(p) se lako vidi raspisivanjem (vodeci clanovi se pokrate). Dakle, slika je potprostor prostora polinoma stupnja najvise n-2, a kako su im dimenzije iste, slika je upravo taj prostor.
Zaboravio sam sliku. Dakle, jezgra je jednodimenzionalna, pa je slika (n-1)-dimnzionalna po teoremu o rangu i defektu. Medjutim, ocito u slici moze biti polinom najvise (n-2)-stupnja. Naime, st(D(p))<st(p) se lako vidi raspisivanjem (vodeci clanovi se pokrate). Dakle, slika je potprostor prostora polinoma stupnja najvise n-2, a kako su im dimenzije iste, slika je upravo taj prostor.
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 11:32 ned, 17. 4. 2005 Naslov: Re: 2. zadatak - rok 7.2.2005 Postano: 11:32 ned, 17. 4. 2005 Naslov: Re: 2. zadatak - rok 7.2.2005 |
    |
|
|
[quote="Tonci"]Dakle, postoji a takav da je p(t+a)=p(t), za sve realne t. To zapravo znaci da je a period polinoma p, a jedini periodicni polinomi su konstantni polinomi (gledamo npr. q(t)=p(t)-p(a) i taj ima prebrojivo mnogo nultocki pa je onda nul-polinom), sto znaci da je jezgra vektorski prostor svih konstatntnih polinoma.[/quote]
cek...znaci...ja sam dobio sljedece:
[latex]p(t+a)-p(t)=0[/latex]
po definiciji linearnog operatora [latex]A(x+y)=A(x)+A(y), \forall x,y \in V[/latex](naravno...ako uzmemo da su [latex]\alpha,\beta=1[/latex]).
[latex]p(t)+p(a)-p(t)=0[/latex]
[latex]p(a)=0[/latex]
dakle...p(a) je nulpolinom. zasto mozemo pretpostavit da je p(t) periodican, odnosno konstantan polinom? pa onda izvuc konstataciju da je i on nulpolinom? ne kuzim ovo zadnje.
| Tonci (napisa): | | Dakle, postoji a takav da je p(t+a)=p(t), za sve realne t. To zapravo znaci da je a period polinoma p, a jedini periodicni polinomi su konstantni polinomi (gledamo npr. q(t)=p(t)-p(a) i taj ima prebrojivo mnogo nultocki pa je onda nul-polinom), sto znaci da je jezgra vektorski prostor svih konstatntnih polinoma. |
cek...znaci...ja sam dobio sljedece:

po definiciji linearnog operatora 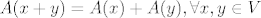 (naravno...ako uzmemo da su (naravno...ako uzmemo da su 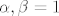 ). ).
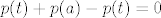
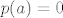
dakle...p(a) je nulpolinom. zasto mozemo pretpostavit da je p(t) periodican, odnosno konstantan polinom? pa onda izvuc konstataciju da je i on nulpolinom? ne kuzim ovo zadnje.
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
 Postano: 13:04 ned, 17. 4. 2005 Naslov: Re: 2. zadatak - rok 7.2.2005 Postano: 13:04 ned, 17. 4. 2005 Naslov: Re: 2. zadatak - rok 7.2.2005 |
    |
|
|
[quote="HijenA"]
cek...znaci...ja sam dobio sljedece:
[latex]p(t+a)-p(t)=0[/latex]
[/quote]
Odavde slijedi da je p(t+a)=p(t) i to treba vrijediti za svaki t. [b]To[/b] znaci da je polinom p periodican, a jedini periodicni polinomi su konstante. Drukciji dokaz ovog ide ovako:
Opet isto, p(t+a)=p(t). Definirajmo polinom q na sljedeci nacin: q(t)=p(t)-p(a). Tada vrijedi q(a)=p(a)-p(a)=0. q(2a)=p(2a)-p(a)=p(a+a)-p(a)=(iz cinjenice da je p(t+a)=p(t))=p(a)-p(a)=0. Slicno q(3a)=q(4a)=...=0. To znaci da polinom q ima "previse" (prebrojivo mnogo) nultocki, a onda je on nul-polinom, tj q(t)=0, za svaki t. Onda je p(t)=p(a) za svaki t, tj p(t) poprima uvijek istu vrijednost (ta vrijednost je p(a)) pa je onda konstantni polinom.
Hope this helps...
| HijenA (napisa): |
cek...znaci...ja sam dobio sljedece:

|
Odavde slijedi da je p(t+a)=p(t) i to treba vrijediti za svaki t. To znaci da je polinom p periodican, a jedini periodicni polinomi su konstante. Drukciji dokaz ovog ide ovako:
Opet isto, p(t+a)=p(t). Definirajmo polinom q na sljedeci nacin: q(t)=p(t)-p(a). Tada vrijedi q(a)=p(a)-p(a)=0. q(2a)=p(2a)-p(a)=p(a+a)-p(a)=(iz cinjenice da je p(t+a)=p(t))=p(a)-p(a)=0. Slicno q(3a)=q(4a)=...=0. To znaci da polinom q ima "previse" (prebrojivo mnogo) nultocki, a onda je on nul-polinom, tj q(t)=0, za svaki t. Onda je p(t)=p(a) za svaki t, tj p(t) poprima uvijek istu vrijednost (ta vrijednost je p(a)) pa je onda konstantni polinom.
Hope this helps...
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 13:36 ned, 17. 4. 2005 Naslov: Re: 2. zadatak - rok 7.2.2005 Postano: 13:36 ned, 17. 4. 2005 Naslov: Re: 2. zadatak - rok 7.2.2005 |
    |
|
|
[quote="Tonci"][quote="HijenA"]
cek...znaci...ja sam dobio sljedece:
[latex]p(t+a)-p(t)=0[/latex]
[/quote]
Odavde slijedi da je p(t+a)=p(t) i to treba vrijediti za svaki t. [b]To[/b] znaci da je polinom p periodican, a jedini periodicni polinomi su konstante. Drukciji dokaz ovog ide ovako:
Opet isto, p(t+a)=p(t). Definirajmo polinom q na sljedeci nacin: q(t)=p(t)-p(a). Tada vrijedi q(a)=p(a)-p(a)=0. q(2a)=p(2a)-p(a)=p(a+a)-p(a)=(iz cinjenice da je p(t+a)=p(t))=p(a)-p(a)=0. Slicno q(3a)=q(4a)=...=0. To znaci da polinom q ima "previse" (prebrojivo mnogo) nultocki, a onda je on nul-polinom, tj q(t)=0, za svaki t. Onda je p(t)=p(a) za svaki t, tj p(t) poprima uvijek istu vrijednost (ta vrijednost je p(a)) pa je onda konstantni polinom.
Hope this helps...[/quote]
ok...shvatio sam (i think). moze jos ovo za sliku? kako znamo da slika ima dimenziju n-2 jer po teoremu o rangu i defektu dimenzija slike je n-1 posto je polinom p(t) sadrzan u slici operatora [latex]D_a[/latex]?
| Tonci (napisa): | | HijenA (napisa): |
cek...znaci...ja sam dobio sljedece:

|
Odavde slijedi da je p(t+a)=p(t) i to treba vrijediti za svaki t. To znaci da je polinom p periodican, a jedini periodicni polinomi su konstante. Drukciji dokaz ovog ide ovako:
Opet isto, p(t+a)=p(t). Definirajmo polinom q na sljedeci nacin: q(t)=p(t)-p(a). Tada vrijedi q(a)=p(a)-p(a)=0. q(2a)=p(2a)-p(a)=p(a+a)-p(a)=(iz cinjenice da je p(t+a)=p(t))=p(a)-p(a)=0. Slicno q(3a)=q(4a)=...=0. To znaci da polinom q ima "previse" (prebrojivo mnogo) nultocki, a onda je on nul-polinom, tj q(t)=0, za svaki t. Onda je p(t)=p(a) za svaki t, tj p(t) poprima uvijek istu vrijednost (ta vrijednost je p(a)) pa je onda konstantni polinom.
Hope this helps... |
ok...shvatio sam (i think). moze jos ovo za sliku? kako znamo da slika ima dimenziju n-2 jer po teoremu o rangu i defektu dimenzija slike je n-1 posto je polinom p(t) sadrzan u slici operatora 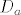 ? ?
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
 Postano: 15:52 ned, 17. 4. 2005 Naslov: Postano: 15:52 ned, 17. 4. 2005 Naslov: |
    |
|
|
Dimenzija od P_n je n (iako su stupnja manjeg od n, tu su i oni stupnja nula). Dakle, dimenzija jezgre + dimenzija slike = n.
Vec smo vidjeli da je dimenzija jezgre 1, dakle, dimenzija slike je n-1.
Poslije dokazem da su slika svi polinomi stupnja najvise (n-2) ali to nije krivo jer je prostor svih tih polinoma (n-1)-dimenzionalan, opet zbog polinoma stupnja nula.
Dimenzija od P_n je n (iako su stupnja manjeg od n, tu su i oni stupnja nula). Dakle, dimenzija jezgre + dimenzija slike = n.
Vec smo vidjeli da je dimenzija jezgre 1, dakle, dimenzija slike je n-1.
Poslije dokazem da su slika svi polinomi stupnja najvise (n-2) ali to nije krivo jer je prostor svih tih polinoma (n-1)-dimenzionalan, opet zbog polinoma stupnja nula.
|
|
| [Vrh] |
|
|













