| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 20:11 ned, 4. 9. 2005 Naslov: Pomoć oko B-W teorema!? |
    |
|
|
Naime, trebao bih pomoć oko dokaza Bolzano-Weierstrassova teorema o neprekidnim funkcijama na segmentu (gradivo MA1) koji glasi: "Neka je I=[a,b] segment realnih brojeva i f sa I u R neprekidna funkcija na I. Ako funkcija f nije konstanta, onda je I'=f(I)={f(x):x element iz I} segment u R." Konkretno, kad dokazujemo ograničenost funkcije f onda u dokazu i u bilježnici i u knjizi piše "Kada bi f bila odozgo neograničena, onda bi za svako n iz N postojao bar jedan element xn iz I takav da je f(xn)>n." Zašto je to tako? Kakve veze imaju f(xn) i n?
Naime, trebao bih pomoć oko dokaza Bolzano-Weierstrassova teorema o neprekidnim funkcijama na segmentu (gradivo MA1) koji glasi: "Neka je I=[a,b] segment realnih brojeva i f sa I u R neprekidna funkcija na I. Ako funkcija f nije konstanta, onda je I'=f(I)={f(x) element iz I} segment u R." Konkretno, kad dokazujemo ograničenost funkcije f onda u dokazu i u bilježnici i u knjizi piše "Kada bi f bila odozgo neograničena, onda bi za svako n iz N postojao bar jedan element xn iz I takav da je f(xn)>n." Zašto je to tako? Kakve veze imaju f(xn) i n?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ahri
Forumaš(ica)
Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
| Postano: 20:32 ned, 4. 9. 2005 Naslov: |
|
|
pa ako je odozgo neogranicena, to znaci da od nekog P postoje svi veci brojevi... hmm, ne znam kako da se izrazim, ali npr pogledaj brojevni pravac... ako kaze da je odozgo neogranicena, tada od neke tocke na brojevnom pravcu, svi desno od te tocke su "sadrzani" (neprekinuta je i neogranicena odozgo).
sorry, stvarno se ne znam izraziti, ali nadam se da me razumijes...
tako da ti ta funkcija sadrzava sve brojeve [P, beskonacno>
i sad je lako... koji god prirodni broj n uzmes, sigurno u tom skupu postoji veci (ako je n<P, onda je P veci, a ako je n>=P, onda je u onom skupu sadrzan npr. n+1).
i sad neki broj koji je veci od n (a takav postoji, i ima ih beskonacno mnogo) oznacis sa x_n.
nadam se da sam pomogao, ali malo sam nerazumljiv...
sorry, stvarno se ne znam izraziti, ali nadam se da me razumijes...
tako da ti ta funkcija sadrzava sve brojeve [P, beskonacno>
i sad je lako... koji god prirodni broj n uzmes, sigurno u tom skupu postoji veci (ako je n<P, onda je P veci, a ako je n>=P, onda je u onom skupu sadrzan npr. n+1).
i sad neki broj koji je veci od n (a takav postoji, i ima ih beskonacno mnogo) oznacis sa x_n.
nadam se da sam pomogao, ali malo sam nerazumljiv...
_________________  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ahri
Forumaš(ica)
Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
| Postano: 0:56 pon, 5. 9. 2005 Naslov: |
|
|
|
[quote="ahri"]to znaci da od nekog P postoje svi veci brojevi...
...
sorry, stvarno se ne znam izraziti, ali nadam se da me razumijes...
tako da ti ta funkcija sadrzava sve brojeve [P, beskonacno>[/quote]
Samo mali ispravak, jer je ovo dosta bitno: [b]sama neogranicenost ne znaci da sadrzava [u]SVE[/u] brojeve [P, beskonacno>[/b], nego za svaki x postoji y takav da je p(y) > p(x) (tj. za svakog postoji neki koji ima vecu sliku). 8)
E, a sada cu odmah reci da je i to krivo, iako djeluje "ocito tocno". :-s Naime, funkcija f(x)=1-1/x ima isto svojstvo, a nije neogranicena. :shock:
Dakle, neogranicenost (odozgo) znaci:
[latex]\displaystyle \forall y \exists x: p(x) > y[/latex] 8)
Naravno, kad se tu umijesa i neprekidnost (i funkcije i domene!), onda se dobije ovo sto je Ahri napisao. 8)
| ahri (napisa): | to znaci da od nekog P postoje svi veci brojevi...
...
sorry, stvarno se ne znam izraziti, ali nadam se da me razumijes...
tako da ti ta funkcija sadrzava sve brojeve [P, beskonacno> |
Samo mali ispravak, jer je ovo dosta bitno: sama neogranicenost ne znaci da sadrzava SVE brojeve [P, beskonacno>, nego za svaki x postoji y takav da je p(y) > p(x) (tj. za svakog postoji neki koji ima vecu sliku). 
E, a sada cu odmah reci da je i to krivo, iako djeluje "ocito tocno".  Naime, funkcija f(x)=1-1/x ima isto svojstvo, a nije neogranicena. 
Dakle, neogranicenost (odozgo) znaci:
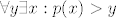
Naravno, kad se tu umijesa i neprekidnost (i funkcije i domene!), onda se dobije ovo sto je Ahri napisao.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
|
