| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 18:21 sri, 23. 11. 2005 Naslov: Re: Par zadačića Postano: 18:21 sri, 23. 11. 2005 Naslov: Re: Par zadačića |
    |
|
|
[quote="Anonymous"]1)od brojeva 1,2,...n nacinimo sve moguce produkte od k različitih faktora.Koliko je takvih brojeva djeljivo s prostim brojem p<=n?[/quote]
Ideja: Za p>n/2 to su oni koji sadrze p. 8) Za p izmedju n/3 i n/2, to su oni koji sadrze p [b]ili[/b] p/2 (ili oba!). :| Dakle, ovisi o "najvece cijelo od n/p". 8)
[quote="Anonymous"]2)neka je A skup kardanaliteta m.Na koliko je nacina moguce odabrati dvoclani skup {x1,x2}iz P(A) takav da je x1Ux2=A?[/quote]
Neka je [latex]A=\{a_0, a_1,\dots,a_{m-1}\}[/latex] i neka je [latex](b_{m-1} \dots b_1b_0)_2[/latex] bin. broj. :)
[latex]b_i = \left\{\begin{array}{l@{\,,\ }l}
0 & a_i \in x1 \\
1 & a_i \in x2
\end{array}\right.[/latex]
Dokazi bijektivnost i vidi koliko ima takvih brojeva. 8)
Treci zadatak ce netko drugi... :gg:
| Anonymous (napisa): | | 1)od brojeva 1,2,...n nacinimo sve moguce produkte od k različitih faktora.Koliko je takvih brojeva djeljivo s prostim brojem p⇐n? |
Ideja: Za p>n/2 to su oni koji sadrze p.  Za p izmedju n/3 i n/2, to su oni koji sadrze p ili p/2 (ili oba!). Za p izmedju n/3 i n/2, to su oni koji sadrze p ili p/2 (ili oba!).  Dakle, ovisi o "najvece cijelo od n/p". Dakle, ovisi o "najvece cijelo od n/p". 
| Anonymous (napisa): | | 2)neka je A skup kardanaliteta m.Na koliko je nacina moguce odabrati dvoclani skup {x1,x2}iz P(A) takav da je x1Ux2=A? |
Neka je 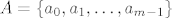 i neka je i neka je  bin. broj. bin. broj. 
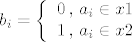
Dokazi bijektivnost i vidi koliko ima takvih brojeva. 
Treci zadatak ce netko drugi... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 22:08 sri, 23. 11. 2005 Naslov: Re: Par zadačića Postano: 22:08 sri, 23. 11. 2005 Naslov: Re: Par zadačića |
    |
|
|
[quote="vsego"][quote="Anonymous"]1)od brojeva 1,2,...n nacinimo sve moguce produkte od k različitih faktora.Koliko je takvih brojeva djeljivo s prostim brojem p<=n?[/quote]
Ideja: Za p>n/2 to su oni koji sadrze p. 8) Za p izmedju n/3 i n/2, to su oni koji sadrze p [b]ili[/b] p/2 (ili oba!). :| Dakle, ovisi o "najvece cijelo od n/p". 8)[/quote]
Druga ideja: bar jedan od faktora mora biti djeljiv s p. Prebroji koliko ima produkata kod kojih nijedan faktor nije djeljiv s p i oduzmi od ukupnog broja.
Cini mi se da p/2 uglavnom nece biti prirodan broj... nije mi bas jasno sto tu radi...
[quote="vsego"][quote="Anonymous"]2)neka je A skup kardanaliteta m.Na koliko je nacina moguce odabrati dvoclani skup {x1,x2}iz P(A) takav da je x1Ux2=A?[/quote]
Neka je [latex]A=\{a_0, a_1,\dots,a_{m-1}\}[/latex] i neka je [latex](b_{m-1} \dots b_1b_0)_2[/latex] bin. broj. :)
[latex]b_i = \left\{\begin{array}{l@{\,,\ }l}
0 & a_i \in x1 \\
1 & a_i \in x2
\end{array}\right.[/latex]
Dokazi bijektivnost i vidi koliko ima takvih brojeva. 8)[/quote]
Ne pise da su x1 i x2 disjunktni. Dakle, za svaki element iz A trebas se odluciti je li u x1, ili u x2, ili u oba. Samo pazi da ne bude x1=x2 (jer onda {x1,x2} nije dvoclan). I podijeli s 2 jer je svejedno koji je prvi a koji drugi.
[quote="vsego"]Treci zadatak ce netko drugi... :gg:[/quote]
Dok kazes :keks:
| vsego (napisa): | | Anonymous (napisa): | | 1)od brojeva 1,2,...n nacinimo sve moguce produkte od k različitih faktora.Koliko je takvih brojeva djeljivo s prostim brojem p⇐n? |
Ideja: Za p>n/2 to su oni koji sadrze p.  Za p izmedju n/3 i n/2, to su oni koji sadrze p ili p/2 (ili oba!). Za p izmedju n/3 i n/2, to su oni koji sadrze p ili p/2 (ili oba!).  Dakle, ovisi o "najvece cijelo od n/p". Dakle, ovisi o "najvece cijelo od n/p".  |
Druga ideja: bar jedan od faktora mora biti djeljiv s p. Prebroji koliko ima produkata kod kojih nijedan faktor nije djeljiv s p i oduzmi od ukupnog broja.
Cini mi se da p/2 uglavnom nece biti prirodan broj... nije mi bas jasno sto tu radi...
| vsego (napisa): | | Anonymous (napisa): | | 2)neka je A skup kardanaliteta m.Na koliko je nacina moguce odabrati dvoclani skup {x1,x2}iz P(A) takav da je x1Ux2=A? |
Neka je 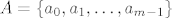 i neka je i neka je  bin. broj. bin. broj. 
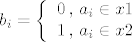
Dokazi bijektivnost i vidi koliko ima takvih brojeva.  |
Ne pise da su x1 i x2 disjunktni. Dakle, za svaki element iz A trebas se odluciti je li u x1, ili u x2, ili u oba. Samo pazi da ne bude x1=x2 (jer onda {x1,x2} nije dvoclan). I podijeli s 2 jer je svejedno koji je prvi a koji drugi.
| vsego (napisa): | Treci zadatak ce netko drugi...  |
Dok kazes 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:44 sri, 23. 11. 2005 Naslov: Re: Par zadačića Postano: 22:44 sri, 23. 11. 2005 Naslov: Re: Par zadačića |
    |
|
|
[quote="krcko"]Cini mi se da p/2 uglavnom nece biti prirodan broj... nije mi bas jasno sto tu radi...[/quote]
2p. :oops:
[quote="krcko"]Ne pise da su x1 i x2 disjunktni. Dakle, za svaki element iz A trebas se odluciti je li u x1, ili u x2, ili u oba. Samo pazi da ne bude x1=x2 (jer onda {x1,x2} nije dvoclan). I podijeli s 2 jer je svejedno koji je prvi a koji drugi.[/quote]
Ok, onda moze preko baze 3, uz oprez da nisu svi u oba skupa, te koji se slucajevi pojavljuju dvaput. ;)
| krcko (napisa): | | Cini mi se da p/2 uglavnom nece biti prirodan broj... nije mi bas jasno sto tu radi... |
2p. 
| krcko (napisa): | | Ne pise da su x1 i x2 disjunktni. Dakle, za svaki element iz A trebas se odluciti je li u x1, ili u x2, ili u oba. Samo pazi da ne bude x1=x2 (jer onda {x1,x2} nije dvoclan). I podijeli s 2 jer je svejedno koji je prvi a koji drugi. |
Ok, onda moze preko baze 3, uz oprez da nisu svi u oba skupa, te koji se slucajevi pojavljuju dvaput. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 22:57 sri, 23. 11. 2005 Naslov: Re: Par zadačića Postano: 22:57 sri, 23. 11. 2005 Naslov: Re: Par zadačića |
    |
|
|
[quote="Anonymous"]3) Koliko ima nesukladnih trokuta opsega 2000,čije su duljine stranica prirodni brojevi?[/quote]
83333, provrtjeh petlju da pobrojim.
Ali to se može dobiti i malo pametnijim prebrajanjem i sumiranjem.
Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko.
Tražimo koliko ima neuređenih trojki prirodnih brojeva a,b,c koji su stranice trokuta i za koje je a+b+c=2000.
Uz supstituciju
x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2
a=y+z, b=z+x, c=x+y
problem prelazi u traženje koliko ima neuređenih trojki prirodnih brojeva x,y,z za koje je x+y+z=1000.
J=broj trojki x,y,z kod kojih su neka dva broja jednaka
R=broj trojki x,y,z kod kojih su svi brojevi različiti
Očigledno je J=499.
Osim toga,
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
Odavde dobivamo
R=499*166
Konačno, traženi broj je
J+R=499*167=83333
| Anonymous (napisa): | | 3) Koliko ima nesukladnih trokuta opsega 2000,čije su duljine stranica prirodni brojevi? |
83333, provrtjeh petlju da pobrojim.
Ali to se može dobiti i malo pametnijim prebrajanjem i sumiranjem.
Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko.
Tražimo koliko ima neuređenih trojki prirodnih brojeva a,b,c koji su stranice trokuta i za koje je a+b+c=2000.
Uz supstituciju
x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2
a=y+z, b=z+x, c=x+y
problem prelazi u traženje koliko ima neuređenih trojki prirodnih brojeva x,y,z za koje je x+y+z=1000.
J=broj trojki x,y,z kod kojih su neka dva broja jednaka
R=broj trojki x,y,z kod kojih su svi brojevi različiti
Očigledno je J=499.
Osim toga,
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
Odavde dobivamo
R=499*166
Konačno, traženi broj je
J+R=499*167=83333
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 11:20 čet, 24. 11. 2005 Naslov: Postano: 11:20 čet, 24. 11. 2005 Naslov: |
    |
|
|
Da se radi o uredenom paru, u prvom zadatku bi imao bijekciju sa [latex] 2 \times m[/latex] matricama nula i jedinica sa svojstvom da nijedan stupac nije nul-stupac (to bi znacilo da neki element ne sadrzi nijedan od dva podskupa). Sad bi bilo dobro kad bi se to moglo upotrijebiti i za skup.
Pogledas skup svih takvih matrica. Ako neka matrica zadovoljava uvjet tada i matrica koju dobijemo zamjenjivanjem redaka te matrice takoder zadovoljava uvjet (to je isto kao i zamjenjivanje mjesta u uredenom paru), no toga se mozemo rijesiti uz dodatan uvjet da je npr broj ciji binaran zapis predstavlja prvi redak strogo veci (tako smo se rrijesili i jedinog slucaja kada su nam retci jednaki, a koji nam nije dobar jer nam skupovi moraju biti razliciti) od onog ciji predstavlja drugi redak.
Uz taj dodatni uvjet na matrice sada imamo pravu bijekciju. Broj nacina za odabir tih matrica bez dodatnog uvjeta je [latex]3^m[/latex] jer za svaki stupac imas tri mogucnosti. Ima samo jedna takva matrica kojoj su oba retka jednaka (matrica puna jedinica), a u svim ostalim slucajevima je za svaku matricu matrica sa zamijenjenim recima razlicita. To znaci da ovaj dodatan uvjet od [latex]3^m[/latex] makne jedan, pa jos prepolovi. Ukupan broj takvih matrica je [latex]\frac{3^m - 1}{2}[/latex], a zbog bijekcije je to ujedno i broj takvih skupova
Da se radi o uredenom paru, u prvom zadatku bi imao bijekciju sa 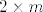 matricama nula i jedinica sa svojstvom da nijedan stupac nije nul-stupac (to bi znacilo da neki element ne sadrzi nijedan od dva podskupa). Sad bi bilo dobro kad bi se to moglo upotrijebiti i za skup. matricama nula i jedinica sa svojstvom da nijedan stupac nije nul-stupac (to bi znacilo da neki element ne sadrzi nijedan od dva podskupa). Sad bi bilo dobro kad bi se to moglo upotrijebiti i za skup.
Pogledas skup svih takvih matrica. Ako neka matrica zadovoljava uvjet tada i matrica koju dobijemo zamjenjivanjem redaka te matrice takoder zadovoljava uvjet (to je isto kao i zamjenjivanje mjesta u uredenom paru), no toga se mozemo rijesiti uz dodatan uvjet da je npr broj ciji binaran zapis predstavlja prvi redak strogo veci (tako smo se rrijesili i jedinog slucaja kada su nam retci jednaki, a koji nam nije dobar jer nam skupovi moraju biti razliciti) od onog ciji predstavlja drugi redak.
Uz taj dodatni uvjet na matrice sada imamo pravu bijekciju. Broj nacina za odabir tih matrica bez dodatnog uvjeta je 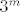 jer za svaki stupac imas tri mogucnosti. Ima samo jedna takva matrica kojoj su oba retka jednaka (matrica puna jedinica), a u svim ostalim slucajevima je za svaku matricu matrica sa zamijenjenim recima razlicita. To znaci da ovaj dodatan uvjet od jer za svaki stupac imas tri mogucnosti. Ima samo jedna takva matrica kojoj su oba retka jednaka (matrica puna jedinica), a u svim ostalim slucajevima je za svaku matricu matrica sa zamijenjenim recima razlicita. To znaci da ovaj dodatan uvjet od 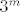 makne jedan, pa jos prepolovi. Ukupan broj takvih matrica je makne jedan, pa jos prepolovi. Ukupan broj takvih matrica je 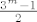 , a zbog bijekcije je to ujedno i broj takvih skupova , a zbog bijekcije je to ujedno i broj takvih skupova
_________________
Bri
|
|
| [Vrh] |
|
Markec
Forumaš(ica)

Pridružen/a: 20. 02. 2003. (14:49:45)
Postovi: (134)16
Spol: 
|
 Postano: 20:38 čet, 24. 11. 2005 Naslov: Postano: 20:38 čet, 24. 11. 2005 Naslov: |
    |
|
|
[quote]
[quote]3) Koliko ima nesukladnih trokuta opsega 2000,čije su duljine stranica prirodni brojevi?[/quote]
83333, provrtjeh petlju da pobrojim.
Ali to se može dobiti i malo pametnijim prebrajanjem i sumiranjem.
Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko.
Tražimo koliko ima neuređenih trojki prirodnih brojeva a,b,c koji su stranice trokuta i za koje je a+b+c=2000.
Uz supstituciju
x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2
a=y+z, b=z+x, c=x+y
problem prelazi u traženje koliko ima neuređenih trojki prirodnih brojeva x,y,z za koje je x+y+z=1000.
J=broj trojki x,y,z kod kojih su neka dva broja jednaka
R=broj trojki x,y,z kod kojih su svi brojevi različiti
Očigledno je J=499.
Osim toga,
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
Odavde dobivamo
R=499*166
Konačno, traženi broj je
J+R=499*167=83333[/quote]
jel tu upada i npr. trojka (1,2,1997)-mislim to npr. nije trokut
| Citat: |
| Citat: | | 3) Koliko ima nesukladnih trokuta opsega 2000,čije su duljine stranica prirodni brojevi? |
83333, provrtjeh petlju da pobrojim.
Ali to se može dobiti i malo pametnijim prebrajanjem i sumiranjem.
Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko.
Tražimo koliko ima neuređenih trojki prirodnih brojeva a,b,c koji su stranice trokuta i za koje je a+b+c=2000.
Uz supstituciju
x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2
a=y+z, b=z+x, c=x+y
problem prelazi u traženje koliko ima neuređenih trojki prirodnih brojeva x,y,z za koje je x+y+z=1000.
J=broj trojki x,y,z kod kojih su neka dva broja jednaka
R=broj trojki x,y,z kod kojih su svi brojevi različiti
Očigledno je J=499.
Osim toga,
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
Odavde dobivamo
R=499*166
Konačno, traženi broj je
J+R=499*167=83333 |
jel tu upada i npr. trojka (1,2,1997)-mislim to npr. nije trokut
|
|
| [Vrh] |
|
Gost
|
 Postano: 21:13 čet, 24. 11. 2005 Naslov: Postano: 21:13 čet, 24. 11. 2005 Naslov: |
    |
|
|
[quote="Markec"]jel tu upada i npr. trojka (1,2,1997)-mislim to npr. nije trokut[/quote]
Pa ne upada. Samo trojke koje su duljine stranica nekog trokuta. Zato i je malo teže za prebrojiti.
Osim toga, to su čak neuređene trojke, npr. 6 permutacija od (500, 600, 900) brojimo samo jedanput, a 3 permutacije od (600, 600, 800) isto samo jedanput.
| Markec (napisa): | | jel tu upada i npr. trojka (1,2,1997)-mislim to npr. nije trokut |
Pa ne upada. Samo trojke koje su duljine stranica nekog trokuta. Zato i je malo teže za prebrojiti.
Osim toga, to su čak neuređene trojke, npr. 6 permutacija od (500, 600, 900) brojimo samo jedanput, a 3 permutacije od (600, 600, 800) isto samo jedanput.
|
|
| [Vrh] |
|
plavooka
Forumaš(ica)


Pridružen/a: 23. 06. 2004. (18:22:48)
Postovi: (43)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
plavooka
Forumaš(ica)


Pridružen/a: 23. 06. 2004. (18:22:48)
Postovi: (43)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
antimon
Forumaš(ica)

Pridružen/a: 01. 03. 2005. (20:28:21)
Postovi: (8)16
|
 Postano: 18:36 pet, 25. 11. 2005 Naslov: Re: Par zadačića Postano: 18:36 pet, 25. 11. 2005 Naslov: Re: Par zadačića |
    |
|
|
[quote="vjekovac"][quote="Anonymous"]3) Koliko ima nesukladnih trokuta opsega 2000,čije su duljine stranica prirodni brojevi?[/quote]
83333, provrtjeh petlju da pobrojim.
Ali to se može dobiti i malo pametnijim prebrajanjem i sumiranjem.
Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko.
Tražimo koliko ima neuređenih trojki prirodnih brojeva a,b,c koji su stranice trokuta i za koje je a+b+c=2000.
Uz supstituciju
x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2
a=y+z, b=z+x, c=x+y
problem prelazi u traženje koliko ima neuređenih trojki prirodnih brojeva x,y,z za koje je x+y+z=1000.
J=broj trojki x,y,z kod kojih su neka dva broja jednaka
R=broj trojki x,y,z kod kojih su svi brojevi različiti
Očigledno je J=499.
Osim toga,
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
Odavde dobivamo
R=499*166
Konačno, traženi broj je
J+R=499*167=83333[/quote]
Lijepo napisano, ali...
Vidim 2 greške: 1. Riječ je o [b]trokutu[/b], pa mora biti zadovoljena i nejednakost trokuta...
2. Trokuti sa stranicama npr. 700/700/600 i 600/700/700 nisu različiti, a prebrojani su...
To je ono što ja vidim i zato mislim da treba doraditi rješenje.
Zadaci su dani na vježbama za rješiti kod kuće. U redu je tražiti pomoć, ali se nadam da ih je netko najprije probao/la sam/a riješiti.
Ja se, istina, još nisam potrudio :oops:
| vjekovac (napisa): | | Anonymous (napisa): | | 3) Koliko ima nesukladnih trokuta opsega 2000,čije su duljine stranica prirodni brojevi? |
83333, provrtjeh petlju da pobrojim.
Ali to se može dobiti i malo pametnijim prebrajanjem i sumiranjem.
Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko.
Tražimo koliko ima neuređenih trojki prirodnih brojeva a,b,c koji su stranice trokuta i za koje je a+b+c=2000.
Uz supstituciju
x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2
a=y+z, b=z+x, c=x+y
problem prelazi u traženje koliko ima neuređenih trojki prirodnih brojeva x,y,z za koje je x+y+z=1000.
J=broj trojki x,y,z kod kojih su neka dva broja jednaka
R=broj trojki x,y,z kod kojih su svi brojevi različiti
Očigledno je J=499.
Osim toga,
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
Odavde dobivamo
R=499*166
Konačno, traženi broj je
J+R=499*167=83333 |
Lijepo napisano, ali...
Vidim 2 greške: 1. Riječ je o trokutu, pa mora biti zadovoljena i nejednakost trokuta...
2. Trokuti sa stranicama npr. 700/700/600 i 600/700/700 nisu različiti, a prebrojani su...
To je ono što ja vidim i zato mislim da treba doraditi rješenje.
Zadaci su dani na vježbama za rješiti kod kuće. U redu je tražiti pomoć, ali se nadam da ih je netko najprije probao/la sam/a riješiti.
Ja se, istina, još nisam potrudio 
_________________
Ja sam uvijek neodlučan! A možda i nisam?!
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 18:43 pet, 25. 11. 2005 Naslov: Postano: 18:43 pet, 25. 11. 2005 Naslov: |
    |
|
|
[quote="vjekovac"]x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2 [/quote]
Nije li nejednakost trokuta postignuta time da su x,y,z [b]prirodni[/b] (dakle [b]nenegativni[/b]) brojevi? :-k
| vjekovac (napisa): | | x=(b+c-a)/2, y=(c+a-b)/2, z=(a+b-c)/2 |
Nije li nejednakost trokuta postignuta time da su x,y,z prirodni (dakle nenegativni) brojevi? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
antimon
Forumaš(ica)


Pridružen/a: 01. 03. 2005. (20:28:21)
Postovi: (8)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 18:16 pon, 28. 11. 2005 Naslov: Postano: 18:16 pon, 28. 11. 2005 Naslov: |
    |
|
|
[quote="antimon"]ali mislim da još uvijek ostaje problem pod brojem 2. Jesam li u pravu? :?[/quote]
Nisu li [b]oba[/b] trokuta sadrzana u 3J? :-k A u konacan rezultat, vjekovac je stavio samo J. 8)
Sorry, ne stignem se bolje udubiti u to, ali meni se cini da je dobro rijesio. :)
| antimon (napisa): | ali mislim da još uvijek ostaje problem pod brojem 2. Jesam li u pravu?  |
Nisu li oba trokuta sadrzana u 3J?  A u konacan rezultat, vjekovac je stavio samo J. A u konacan rezultat, vjekovac je stavio samo J. 
Sorry, ne stignem se bolje udubiti u to, ali meni se cini da je dobro rijesio. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 21:01 pon, 28. 11. 2005 Naslov: Re: Par zadačića Postano: 21:01 pon, 28. 11. 2005 Naslov: Re: Par zadačića |
    |
|
|
[quote="antimon"]1. Riječ je o [b]trokutu[/b], pa mora biti zadovoljena i nejednakost trokuta...[/quote]
Kao što reče vsego. Tome i služi gornja supstitucija.
[quote="antimon"]2. Trokuti sa stranicama npr. 700/700/600 i 600/700/700 nisu različiti, a prebrojani su...[/quote]
U jednakosti:
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
su raznostranični trokuti prebrojani 6 puta, a jednakokračni 3 puta.
No ja na kraju računam R+J i to je broj svih trokuta, pri čemu je svaki uračunat jedanput.
Zato sam i napisao ovo:
[quote="ja"]Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko.[/quote]
Malo povjerenja molim. Nisam ja baš od jučer. 8)
Ima tu još dosta sitnica za raspisati kad čovjek ide cjepidlačiti. Ali onda to više ne bi bilo elegantno rješenje.
| antimon (napisa): | | 1. Riječ je o trokutu, pa mora biti zadovoljena i nejednakost trokuta... |
Kao što reče vsego. Tome i služi gornja supstitucija.
| antimon (napisa): | | 2. Trokuti sa stranicama npr. 700/700/600 i 600/700/700 nisu različiti, a prebrojani su... |
U jednakosti:
6R+3J = broj rastava od 1000 na 3 prirodna pribrojnika = (999 povrh 2)
su raznostranični trokuti prebrojani 6 puta, a jednakokračni 3 puta.
No ja na kraju računam R+J i to je broj svih trokuta, pri čemu je svaki uračunat jedanput.
Zato sam i napisao ovo:
| ja (napisa): | | Evo mog rješenja koje koristi ipak malo sofisticiraniju ideju (i treba se malo nad njim zamisliti da bi mu se povjerovalo), ali je kratko. |
Malo povjerenja molim. Nisam ja baš od jučer. 
Ima tu još dosta sitnica za raspisati kad čovjek ide cjepidlačiti. Ali onda to više ne bi bilo elegantno rješenje.
|
|
| [Vrh] |
|
antimon
Forumaš(ica)


Pridružen/a: 01. 03. 2005. (20:28:21)
Postovi: (8)16
|
|
| [Vrh] |
|
|













