| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 20:30 uto, 10. 1. 2006 Naslov: Zadatak sa kolokvija Postano: 20:30 uto, 10. 1. 2006 Naslov: Zadatak sa kolokvija |
    |
|
|
Ako netko zna kako se rjesava ovaj zadatak molim da napise rjesenje i objasni:
Neka je omega= { 1, 2, 3, 4, 5, 6, 7 } i A1 = { 1, 2 } , A2 = { 3, 5, 6 } , A3 = { 4 } , A4 = { 7 } . Odredite najmanju sigma−algebru na omega
koja sadrzi skupove Ai, i = 1, 2, 3, 4.
Puno hvala!:-)
Ako netko zna kako se rjesava ovaj zadatak molim da napise rjesenje i objasni:
Neka je omega= { 1, 2, 3, 4, 5, 6, 7 } i A1 = { 1, 2 } , A2 = { 3, 5, 6 } , A3 = { 4 } , A4 = { 7 } . Odredite najmanju sigma−algebru na omega
koja sadrzi skupove Ai, i = 1, 2, 3, 4.
Puno hvala!
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 21:28 uto, 10. 1. 2006 Naslov: Postano: 21:28 uto, 10. 1. 2006 Naslov: |
    |
|
|
Probaš napraviti najmanju familiju tako da vrijedi:
(iz definicije)
1. prazan skup je u familiji
2. Za svaki skup iz familije, i njegov komplement je u familiji
3. Svaka prebrojiva unija skupova iz familije je opet element familije
I sad se trebaš igrat s tim pravilima. Za ovaj konkretan primjer, ubaciš prazan skup, svaki pojedini A_1,.. ,A_4 i sve njihove unije (za to sigurno znaš da mora biti u familiji da bi to bila sigma-algebra) i provjeriš da je to sve što ti treba(da su zadovoljena sva tri uvjeta iz definicije). Dobit ćeš ukupno 16 skupova (2^4 :) )
Ali ne nalaziš ih uvijek na taj način, ovdje je to tako zato što su skupovi A_1,...,A_4 međusobno disjunktni.
Kao što rekoh, inače se igraš s tim pravilima da bi dobio takve nekakve disjunktne skupove koji su sigurno u familiji.
Hope it helps! :wink:
Probaš napraviti najmanju familiju tako da vrijedi:
(iz definicije)
1. prazan skup je u familiji
2. Za svaki skup iz familije, i njegov komplement je u familiji
3. Svaka prebrojiva unija skupova iz familije je opet element familije
I sad se trebaš igrat s tim pravilima. Za ovaj konkretan primjer, ubaciš prazan skup, svaki pojedini A_1,.. ,A_4 i sve njihove unije (za to sigurno znaš da mora biti u familiji da bi to bila sigma-algebra) i provjeriš da je to sve što ti treba(da su zadovoljena sva tri uvjeta iz definicije). Dobit ćeš ukupno 16 skupova (2^4  ) )
Ali ne nalaziš ih uvijek na taj način, ovdje je to tako zato što su skupovi A_1,...,A_4 međusobno disjunktni.
Kao što rekoh, inače se igraš s tim pravilima da bi dobio takve nekakve disjunktne skupove koji su sigurno u familiji.
Hope it helps! 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
akki
Forumaš(ica)


Pridružen/a: 28. 09. 2004. (14:55:35)
Postovi: (88)16
|
 Postano: 16:07 sri, 11. 1. 2006 Naslov: Postano: 16:07 sri, 11. 1. 2006 Naslov: |
    |
|
|
Ja sam dobila samo 10 skupova :? , i to slijedeće: {1,2}, {3,5,6}, {4}, {7}, {3,4,5,6}, {1,2,4,7}, {1,2,3,5,6,7}, {1,2,3,4,5,6}, {1,2,3,4,5,6,7} i prazan skup. Dali netko zna gdje grješim :x
Ja sam dobila samo 10 skupova  , i to slijedeće: {1,2}, {3,5,6}, {4}, {7}, {3,4,5,6}, {1,2,4,7}, {1,2,3,5,6,7}, {1,2,3,4,5,6}, {1,2,3,4,5,6,7} i prazan skup. Dali netko zna gdje grješim , i to slijedeće: {1,2}, {3,5,6}, {4}, {7}, {3,4,5,6}, {1,2,4,7}, {1,2,3,5,6,7}, {1,2,3,4,5,6}, {1,2,3,4,5,6,7} i prazan skup. Dali netko zna gdje grješim 
_________________ 
 Kad jednom probas letjeti
hodati ces zemljom, s pogledom prema gore,
tamo gdje si bio i kamo se čezneš vratiti....
  |
|
| [Vrh] |
|
Kova
Forumaš(ica)


Pridružen/a: 27. 02. 2004. (23:13:50)
Postovi: (4B)16
Spol: 
|
 Postano: 17:45 sri, 11. 1. 2006 Naslov: Postano: 17:45 sri, 11. 1. 2006 Naslov: |
    |
|
|
[quote="akki"]Ja sam dobila samo 10 skupova Confused , i to slijedeće: {1,2}, {3,5,6}, {4}, {7}, {3,4,5,6}, {1,2,4,7}, {1,2,3,5,6,7}, {1,2,3,4,5,6}, {1,2,3,4,5,6,7} i prazan skup. Dali netko zna gdje grješim Mad[/quote]
Fali ti A1UA3={1,2,4}, A1UA4={1,2,7}, A1UA2={1,2,3,5,6}, A2UA4={3,5,6,7}, A3UA4={4,7}, A1UA2UA4={1,2,3,5,6,7}
eto mislim da su to svi (uz one koje si ti navela), nadam se da nisam falio :)
:lol:
| akki (napisa): | | Ja sam dobila samo 10 skupova Confused , i to slijedeće: {1,2}, {3,5,6}, {4}, {7}, {3,4,5,6}, {1,2,4,7}, {1,2,3,5,6,7}, {1,2,3,4,5,6}, {1,2,3,4,5,6,7} i prazan skup. Dali netko zna gdje grješim Mad |
Fali ti A1UA3={1,2,4}, A1UA4={1,2,7}, A1UA2={1,2,3,5,6}, A2UA4={3,5,6,7}, A3UA4={4,7}, A1UA2UA4={1,2,3,5,6,7}
eto mislim da su to svi (uz one koje si ti navela), nadam se da nisam falio 

_________________
kova
|
|
| [Vrh] |
|
akki
Forumaš(ica)


Pridružen/a: 28. 09. 2004. (14:55:35)
Postovi: (88)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:27 sri, 11. 1. 2006 Naslov: Postano: 20:27 sri, 11. 1. 2006 Naslov: |
    |
|
|
[quote="akki"]Ako je P(A)=0 ili 1, dokažite da je tada događaj A nezavisan s proizvoljnim događajem B[/quote]
Dogadjaji A i B su nezavisni akko je [latex]P(A \cap B) = P(A) \cdot P(B)[/latex] 8)
Podsjetnik:[list][*][latex]C \subseteq D \Rightarrow 0 \leq P(C) \leq P(D)[/latex]
[*][latex]P(C \cup D) = P(C) + P(D) - P(C \cap D)[/latex] :arrow: [latex]P(C \cup D) + P(C \cap D) = P(C) + P(D)[/latex][/list:u]Nadalje:[list=1][*] Uvrstimo: [latex]P(A) = 0[/latex]
Zbog [latex]A \cap B \subseteq A[/latex] je [latex]P(A \cap B) = 0[/latex].
Takodjer: [latex]P(A) \cdot P(B) = 0 \cdot P(B) = 0[/latex], pa je [latex]P(A \cap B) = P(A) \cdot P(B)[/latex] :D
[*] Uvrstimo: [latex]P(A) = 1[/latex]; vrijedi: [latex]P(A \cap B) + P(A \cup B) = P(A) + P(B) = 1 + P(B)[/latex] i [latex]P(A \cup B) \geq P(A) = 1[/latex], pa je:
[latex]P(A \cap B) + 1 = 1 + P(B)[/latex], tj.
Dakle: [latex]P(A \cap B) = P(B)[/latex]
Takodjer: [latex]P(A) \cdot P(B) = 1 \cdot P(B) = P(B)[/latex], pa je [latex]P(A \cap B) = P(A) \cdot P(B)[/latex] :D[/list:o]
Nadam se da nisam nista fulao... O:)
| akki (napisa): | | Ako je P(A)=0 ili 1, dokažite da je tada događaj A nezavisan s proizvoljnim događajem B |
Dogadjaji A i B su nezavisni akko je 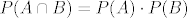 
Podsjetnik:Nadalje:- Uvrstimo:
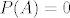
Zbog 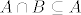 je je 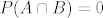 . .
Takodjer: 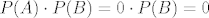 , pa je , pa je 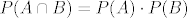 
- Uvrstimo:
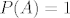 ; vrijedi: ; vrijedi: 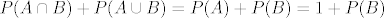 i i 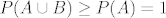 , pa je: , pa je:
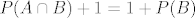 , tj. , tj.
Dakle: 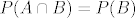
Takodjer: 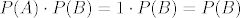 , pa je , pa je 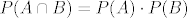 
Nadam se da nisam nista fulao... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
|







