Uzmimo da trokut ima osnovicu a, krakove b, a radijus opisane kruznice R. Opseg je funkcija dviej varijable- a i b. Medutim, 1)jos ne znamo racunati ekstreme funkcija dviju varijabli 2)te dvije varijable nisu nezavisne (ne mogu mijenjati a, ostaviti b fiksan, a da mi trokut ostaje upisan u kruznicu radijusa R). Zato prvo moramo izraziti a preko b (ili obratno), koristeci ovo o R. Ja sam to napravila preko povrsina-vjerojatno moze i drukcije. Dakle, [latex]\frac{ab^{2}}{4R}=P=\frac{1}{2}a\sqrt{b^{2}-\frac{a^{2}}{4}}[/latex]. Iz toga mogu izraziti npr. [latex]a=\sqrt{4b^{2}-\frac{b^{4}}{R^{2}}}[/latex].
Sad mi je opseg [latex]O=a+2b=2b+\sqrt{4b^{2}-\frac{b^{4}}{R^{2}}}[/latex] funkcija jedne varijable (b). Funkciji jedne varijable znam naci ekstrem. Trazim nultocku derivacije [latex]O'=2+\frac{8b-\frac{4b^{3}}{R^{2}}}{2\sqrt{4b^{2}-\frac{b^{4}}{R^{2}}}}=0[/latex]. Kad malo sredim tu jednadzbu, dobivam [latex] \frac{b^{2}}{R^{2}}(\frac{b^{2}}{R^{2}}-3)=0 [/latex]. Rjesenje b=0 bas i nema smisla (zapravo ima, onda je i a=0 i to je trokut s minimalnim opsegom upisan u tu kruznicu :D ), a kad ovo drugo, [latex]b=\sqrt{3}R[/latex] uvrstim u gornju formulu za a, dobivam a=b.
Sad bi jos trebalo komentirati da je ta stacionarna tocka koju smo nasli stvarno tocka maksimuma (a ne npr. minimum ili samo stac.tocka)... A tu morate pitat svoje asistente jel kupuju objanjenje "vidi se sa slike" ili ne :) Evo npr. objasnjenja: to je jedini kandidat za maksimum te funkcije, sa slike je ocito da se maksimum postize, dakle to je maksimum. Asistenti jel kupujete? :)
Uzmimo da trokut ima osnovicu a, krakove b, a radijus opisane kruznice R. Opseg je funkcija dviej varijable- a i b. Medutim, 1)jos ne znamo racunati ekstreme funkcija dviju varijabli 2)te dvije varijable nisu nezavisne (ne mogu mijenjati a, ostaviti b fiksan, a da mi trokut ostaje upisan u kruznicu radijusa R). Zato prvo moramo izraziti a preko b (ili obratno), koristeci ovo o R. Ja sam to napravila preko povrsina-vjerojatno moze i drukcije. Dakle,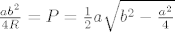 
. Iz toga mogu izraziti npr. 
.
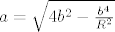Sad mi je opseg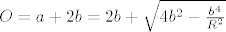 
funkcija jedne varijable (b). Funkciji jedne varijable znam naci ekstrem. Trazim nultocku derivacije 
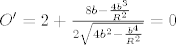. Kad malo sredim tu jednadzbu, dobivam 
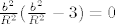. Rjesenje b=0 bas i nema smisla (zapravo ima, onda je i a=0 i to je trokut s minimalnim opsegom upisan u tu kruznicu 
), a kad ovo drugo, 
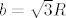uvrstim u gornju formulu za a, dobivam a=b.
Sad bi jos trebalo komentirati da je ta stacionarna tocka koju smo nasli stvarno tocka maksimuma (a ne npr. minimum ili samo stac.tocka)... A tu morate pitat svoje asistente jel kupuju objanjenje "vidi se sa slike" ili ne 
Evo npr. objasnjenja: to je jedini kandidat za maksimum te funkcije, sa slike je ocito da se maksimum postize, dakle to je maksimum. Asistenti jel kupujete?
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
