| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
BoMark
Forumaš(ica)


Pridružen/a: 17. 11. 2003. (12:51:47)
Postovi: (125)16
Spol: 
|
 Postano: 16:51 ned, 29. 1. 2006 Naslov: zadatak:U kruznicu upisan trokut. Poznato: r, a i b. Postano: 16:51 ned, 29. 1. 2006 Naslov: zadatak:U kruznicu upisan trokut. Poznato: r, a i b. |
    |
|
|
Uglavnom, u kruznicu je upisan trokut. Poznat je radijus kruznice r, i dvije stranice trokuta, a i b.
problem je pronaci trecu stranicu trokuta i sve kuteve trokuta.
Molim pomoc u vezi ovog zadatka.
To je gradivo drugog razreda srednje skole...
ako sam na krivom mjestu pitao, molim cijenjene moderatore da premjeste na adekvatno mjesto..
Hvala...
(inace r = 3.6 cm, a = 5, b = 5.8 cm ... ako me sjecanje dobro sluzi)
Uglavnom, u kruznicu je upisan trokut. Poznat je radijus kruznice r, i dvije stranice trokuta, a i b.
problem je pronaci trecu stranicu trokuta i sve kuteve trokuta.
Molim pomoc u vezi ovog zadatka.
To je gradivo drugog razreda srednje skole...
ako sam na krivom mjestu pitao, molim cijenjene moderatore da premjeste na adekvatno mjesto..
Hvala...
(inace r = 3.6 cm, a = 5, b = 5.8 cm ... ako me sjecanje dobro sluzi)
_________________
Ljudi misle da razmisljaju, dok zapravo samo preuredjuju svoje predrasude!
Čovjek koji ne mijenja svoje stavove, nije ljudsko biće nego spomenik!
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 17:09 ned, 29. 1. 2006 Naslov: Postano: 17:09 ned, 29. 1. 2006 Naslov: |
    |
|
|
"Zute" tablice imaju ove formule za povrsinu trokuta:
[latex]P = \frac{abc}{4R} = \sqrt{s(s-a)(s-b)(s-c)}[/latex], gdje je [i]R[/i] radijus opisane kriznice, a [latex]2s = a+b+c[/latex].
Ti imas sve osim [i]c[/i]:
[latex]a^2 b^2 c^2 = R^2 (a+b+c)(-a+b+c)(a-b+c)(a+b-c)[/latex]
[latex]841 c^2 = 12.96 (10.8+c)(0.8+c)(-0.8+c)(10.8-c)[/latex]
S desne strane imas dvije razlike kvadrata:
[latex]841 c^2 = 12.96 (10.8^2-c^2)(c^2-0.8^2)[/latex]
[latex]841 c^2 = 12.96 (116.64-c^2)(c^2-0.64)[/latex]
[latex]841 c^2 = -967.458816 + 1519.9488 c^2 - 12.96 c^4[/latex]
Stavi da je [latex]t := c^2[/latex] i imas obicnu kvadratnu jednadzbu (jasno, ako nisam fulao negdje). :)
Joj, kako ce me Martina tuć' kad vidi kako sam ovo skomplicirao... :trema:
"Zute" tablice imaju ove formule za povrsinu trokuta:
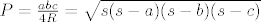 , gdje je R radijus opisane kriznice, a , gdje je R radijus opisane kriznice, a 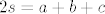 . .
Ti imas sve osim c:

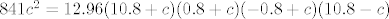
S desne strane imas dvije razlike kvadrata:
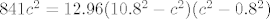
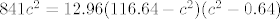
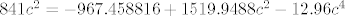
Stavi da je 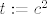 i imas obicnu kvadratnu jednadzbu (jasno, ako nisam fulao negdje). i imas obicnu kvadratnu jednadzbu (jasno, ako nisam fulao negdje). 
Joj, kako ce me Martina tuć' kad vidi kako sam ovo skomplicirao... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 20:50 ned, 29. 1. 2006 Naslov: Postano: 20:50 ned, 29. 1. 2006 Naslov: |
    |
|
|
Tuci ce te Martinab svakako.
[quote="BoMark"] ...u kruznicu je upisan trokut... [/quote]
[quote="vsego"] ...gdje je R radijus opisane kriznice... [/quote]
ccc... Dakle, ako stvarno imas UPISANU kruznicu, odgovarajuca formula za povrsinu je P=rs, uz iste oznake kao dolje. Sad mozes nastaviti kao sto je vsego napisao, izjednacavajuce Heronovu formulu za povrsinu sa ovom koju sam ja napisala gore...
Medutim, u ovom slucaju ne dobivas bikvadratnu jednadzbu po c, nego ti se pojave clanovi 4.,2., 1. i 0. stupnja, kojoj koeficijenti (barem kolko ja vidim), nisu nastimani-> ne znamo ju rijesiti.
Stovise, sumnjiv mi je zadatak :) Tocnije, sumnjivo mi je sto radi u 2. razredu srednje. U 2. srednje bi se trbala raditi stereometrija i trigonometrija, ali samo pravokutnog trokuta. Ovo mi nekak ne spada tu. Ako se program promijenio i u 2. se redi trigonometrija opcenito, onda imamo hrpu trigonometrijskih formula kojima ovo prilicno lako rijesimo...
Ajd pliz provjeri jel fakat 2. razred i kaj sve smijem koristiti (preciznije, jesu li ucili trigonometriju, i da li samo pravokutnog trokuta ili i opcenito- ono, poucak o sinusu i kosinusu i sve sto slijedi iz toga)
Tuci ce te Martinab svakako.
| BoMark (napisa): | | ...u kruznicu je upisan trokut... |
| vsego (napisa): | | ...gdje je R radijus opisane kriznice... |
ccc... Dakle, ako stvarno imas UPISANU kruznicu, odgovarajuca formula za povrsinu je P=rs, uz iste oznake kao dolje. Sad mozes nastaviti kao sto je vsego napisao, izjednacavajuce Heronovu formulu za povrsinu sa ovom koju sam ja napisala gore...
Medutim, u ovom slucaju ne dobivas bikvadratnu jednadzbu po c, nego ti se pojave clanovi 4.,2., 1. i 0. stupnja, kojoj koeficijenti (barem kolko ja vidim), nisu nastimani-> ne znamo ju rijesiti.
Stovise, sumnjiv mi je zadatak  Tocnije, sumnjivo mi je sto radi u 2. razredu srednje. U 2. srednje bi se trbala raditi stereometrija i trigonometrija, ali samo pravokutnog trokuta. Ovo mi nekak ne spada tu. Ako se program promijenio i u 2. se redi trigonometrija opcenito, onda imamo hrpu trigonometrijskih formula kojima ovo prilicno lako rijesimo... Tocnije, sumnjivo mi je sto radi u 2. razredu srednje. U 2. srednje bi se trbala raditi stereometrija i trigonometrija, ali samo pravokutnog trokuta. Ovo mi nekak ne spada tu. Ako se program promijenio i u 2. se redi trigonometrija opcenito, onda imamo hrpu trigonometrijskih formula kojima ovo prilicno lako rijesimo...
Ajd pliz provjeri jel fakat 2. razred i kaj sve smijem koristiti (preciznije, jesu li ucili trigonometriju, i da li samo pravokutnog trokuta ili i opcenito- ono, poucak o sinusu i kosinusu i sve sto slijedi iz toga)
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:36 ned, 29. 1. 2006 Naslov: Postano: 21:36 ned, 29. 1. 2006 Naslov: |
    |
|
|
:zbunjen: Ok, u mojim godinama [ :djed: ] senilija je ozbiljna bolest, ali ako je [b]u kruznicu[/b] upisan trokut, nije li onda ta ista kruznica [b]opisana[/b] tom istom trokutu? :grebgreb:
 Ok, u mojim godinama [ Ok, u mojim godinama [  ] senilija je ozbiljna bolest, ali ako je u kruznicu upisan trokut, nije li onda ta ista kruznica opisana tom istom trokutu? ] senilija je ozbiljna bolest, ali ako je u kruznicu upisan trokut, nije li onda ta ista kruznica opisana tom istom trokutu? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Maroje
Forumaš(ica)

Pridružen/a: 20. 03. 2003. (08:49:56)
Postovi: (8F)16
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 23:32 ned, 29. 1. 2006 Naslov: Postano: 23:32 ned, 29. 1. 2006 Naslov: |
    |
|
|
Gradivo osnovne škole:
Trokut upisan u kružnicu, čija je jedna stranica DIJAGONALA kruga, je pravokutan
(poseban slučaj priče o obodnom i središnjem kutu).
A sada ja vidim DVA pravokutna trokuta, oboma je jedna stranica DIJAGONALA,
a druga poznata stranica trokuta - i tu mi je trigonometrija pravokutnog trokuta dovoljna,
barem da odredim kut između poznatih stranica, a onda koristeći obodni i središnji kut
mislim da imam sve kutove.
Kako na forumu nema tehnoloških mogućnosti za geometrijske konstrukcije :), to ja
ovdje stajem. Nadam se da je ideja korisna.
- Nenad
Gradivo osnovne škole:
Trokut upisan u kružnicu, čija je jedna stranica DIJAGONALA kruga, je pravokutan
(poseban slučaj priče o obodnom i središnjem kutu).
A sada ja vidim DVA pravokutna trokuta, oboma je jedna stranica DIJAGONALA,
a druga poznata stranica trokuta - i tu mi je trigonometrija pravokutnog trokuta dovoljna,
barem da odredim kut između poznatih stranica, a onda koristeći obodni i središnji kut
mislim da imam sve kutove.
Kako na forumu nema tehnoloških mogućnosti za geometrijske konstrukcije  , to ja , to ja
ovdje stajem. Nadam se da je ideja korisna.
- Nenad
|
|
| [Vrh] |
|
BoMark
Forumaš(ica)


Pridružen/a: 17. 11. 2003. (12:51:47)
Postovi: (125)16
Spol: 
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 1:09 pon, 30. 1. 2006 Naslov: Postano: 1:09 pon, 30. 1. 2006 Naslov: |
    |
|
|
ne znam da li se poopceno dijagonalom smatraju spojnice najudaljenijih tocaka... but...
no u ovom gore slucaju se misli na promjer (dijametar, 2radijusa) vulgaris... i talesov poucak o obodnom i sredisnjem kutu, koji specijalno vristi da trokut kojem je jedna stranica promjer kruznice, a nasuprotni vrh na kruznici - je pravokutan sa pravim kutem kod tog nasuprotnog vrha....
talesov poucak opcenito kaze da je je obodni kut nad nekim lukom duplo manji od njemu pripadnog sredisnjeg.... sredisnji je onaj koji spaja krajeve luka sa sredistem kruznice, a obodni je svaki onaj (primjeti, ima ih beskonacno) koji spaja krajeve luka sa tockom na onom dijelu kruznice izvan tog luka....
crtezom: (citaj: zanemari ono gore ako si se pogubio, iako to nije clanak-stavak sistem :wink:)
plavo zeleni trokut je pravokutan - specijalni slucaj, ovo sto tebi treba...
[img]http://www.math.ubc.ca/~hoek/Teaching/Elemgeo/GeoBasic/thal00.jpg[/img]
plavo zeleni kut (obodni )je duplo manji od crveno zutog (sredisnji) kuta
[img]http://www.math.ubc.ca/~hoek/Teaching/Elemgeo/GeoBasic/thal01.jpg[/img]
oba su nad istim lukom, tetivom, isjeckom - ono crno... pa neki dio toga :o) isjecak je sve, luk je dio kruznice, a tetiva je duzina...
nadam se da rasvjetlih i neprezakomplicirah.... :grebgreb:
link, mozda nadjes jos neki odnos koji ti moze koristiti....
[url]http://www.math.ubc.ca/~hoek/Teaching/Elemgeo/Angonseg.html[/url]
ne znam da li se poopceno dijagonalom smatraju spojnice najudaljenijih tocaka... but...
no u ovom gore slucaju se misli na promjer (dijametar, 2radijusa) vulgaris... i talesov poucak o obodnom i sredisnjem kutu, koji specijalno vristi da trokut kojem je jedna stranica promjer kruznice, a nasuprotni vrh na kruznici - je pravokutan sa pravim kutem kod tog nasuprotnog vrha....
talesov poucak opcenito kaze da je je obodni kut nad nekim lukom duplo manji od njemu pripadnog sredisnjeg.... sredisnji je onaj koji spaja krajeve luka sa sredistem kruznice, a obodni je svaki onaj (primjeti, ima ih beskonacno) koji spaja krajeve luka sa tockom na onom dijelu kruznice izvan tog luka....
crtezom: (citaj: zanemari ono gore ako si se pogubio, iako to nije clanak-stavak sistem  ) )
plavo zeleni trokut je pravokutan - specijalni slucaj, ovo sto tebi treba...
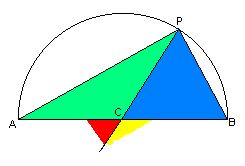
plavo zeleni kut (obodni )je duplo manji od crveno zutog (sredisnji) kuta
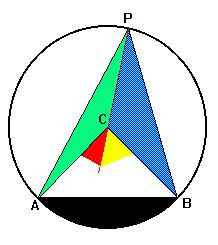
oba su nad istim lukom, tetivom, isjeckom - ono crno... pa neki dio toga  isjecak je sve, luk je dio kruznice, a tetiva je duzina... isjecak je sve, luk je dio kruznice, a tetiva je duzina...
nadam se da rasvjetlih i neprezakomplicirah.... 
link, mozda nadjes jos neki odnos koji ti moze koristiti....
http://www.math.ubc.ca/~hoek/Teaching/Elemgeo/Angonseg.html
_________________
It's not who you love. It's how.
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 10:00 pon, 30. 1. 2006 Naslov: Postano: 10:00 pon, 30. 1. 2006 Naslov: |
    |
|
|
Na prvoj Nesinoj slici, trokut PAB je pravokutan. Uzmimo da je PA jedna stranica
zadanog trokuta, i odmah znamo kosinus kuta kod A.
Zamislimo da je iz točke A nanesena i druga poznata stranica trokuta, čiji drugi
kraj na kružnici označimo s P' (zamislimo s druge strane dijagonale od P), koja s danom
dijagonalom ponovno zatvara poznati kut (kosinus); zbroj ili razlika tih kutova je
tada kut između dviju stranica polaznog trokuta, zovimo ga alpha.
Ostali se kutovi sada lako izračunaju, jer spojnica PP' s C čini jednakokračni trokut,
i kutovi kod P i P' su polovica Pi-(2alpha), tj. Pi/2-alpha.
Duljina stranice PP' se sada lako izračuna preko polumjera upisane kružnice ili
nekako drugačije.
Zaključak: Zadatak je rješiv s pomoću gradiva do trigonometrije pravokutnog trokuta
(uključivo).
- Nenad
Na prvoj Nesinoj slici, trokut PAB je pravokutan. Uzmimo da je PA jedna stranica
zadanog trokuta, i odmah znamo kosinus kuta kod A.
Zamislimo da je iz točke A nanesena i druga poznata stranica trokuta, čiji drugi
kraj na kružnici označimo s P' (zamislimo s druge strane dijagonale od P), koja s danom
dijagonalom ponovno zatvara poznati kut (kosinus); zbroj ili razlika tih kutova je
tada kut između dviju stranica polaznog trokuta, zovimo ga alpha.
Ostali se kutovi sada lako izračunaju, jer spojnica PP' s C čini jednakokračni trokut,
i kutovi kod P i P' su polovica Pi-(2alpha), tj. Pi/2-alpha.
Duljina stranice PP' se sada lako izračuna preko polumjera upisane kružnice ili
nekako drugačije.
Zaključak: Zadatak je rješiv s pomoću gradiva do trigonometrije pravokutnog trokuta
(uključivo).
- Nenad
|
|
| [Vrh] |
|
Maroje
Forumaš(ica)

Pridružen/a: 20. 03. 2003. (08:49:56)
Postovi: (8F)16
|
|
| [Vrh] |
|
BoMark
Forumaš(ica)


Pridružen/a: 17. 11. 2003. (12:51:47)
Postovi: (125)16
Spol: 
|
|
| [Vrh] |
|
|










