| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 20:34 čet, 9. 2. 2006 Naslov: Postano: 20:34 čet, 9. 2. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Uh,sorry zaboravih napisat :oops: : treba naci sve polinome f iz R[x] koji zadovoljavaju x(x-1)f(x+1)=(x-2)(x+1)f(x-1),za svako x iz R[/quote]
Uzmemo [latex]x = 2 \Rightarrow f(3) = 0[/latex]
Tvrdimo da je za svaki x oblika 3 + 2n , [latex]n \in N_0[/latex], f(x) = 0
Lako se pokaze indukcijom po n.
Ako postoji polinom f koji je rjesenje, on ima beskonacno mnogo nultocki, tj f je nul-polinom.
Nul-polinom stvarno zadovoljava gornji uvjet, pa imamo [latex]f(x) = 0[/latex]
| Anonymous (napisa): | Uh,sorry zaboravih napisat  : treba naci sve polinome f iz R[x] koji zadovoljavaju x(x-1)f(x+1)=(x-2)(x+1)f(x-1),za svako x iz R : treba naci sve polinome f iz R[x] koji zadovoljavaju x(x-1)f(x+1)=(x-2)(x+1)f(x-1),za svako x iz R |
Uzmemo 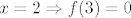
Tvrdimo da je za svaki x oblika 3 + 2n , 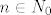 , f(x) = 0 , f(x) = 0
Lako se pokaze indukcijom po n.
Ako postoji polinom f koji je rjesenje, on ima beskonacno mnogo nultocki, tj f je nul-polinom.
Nul-polinom stvarno zadovoljava gornji uvjet, pa imamo 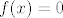
_________________
Bri
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
 Postano: 10:55 pet, 10. 2. 2006 Naslov: Postano: 10:55 pet, 10. 2. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Ako je p polinom s cjelobrojnim koeficijentima koji poprima vrijednost 5 za 5 različitih cijelih brojeva,dokažite da tada p nema cjelobrojnu nultočku![/quote]
Dakle, P(a)=P(b)=P(c)=P(d)=P(e)=5 za medjusobno različite cijele brojeve a,b,c,d,e.
[quote="Anonymous"]Zadatak je s prijašnjih kolokvija i pise da se od p oduzme 5 pa ce sve bit jasnije??[/quote]
Dakle promatramo polinom Q definiran ovako: Q(x)=P(x)-5.
Sada vrijedi Q(a)=Q(b)=Q(c)=Q(d)=Q(e)=0.
Treba pokazati da ne postoji cjelobrojna točka u kojoj Q ima vrijednost -5 (u toj bi točki vrijednost od P bila 0).
Mea
| Anonymous (napisa): | | Ako je p polinom s cjelobrojnim koeficijentima koji poprima vrijednost 5 za 5 različitih cijelih brojeva,dokažite da tada p nema cjelobrojnu nultočku! |
Dakle, P(a)=P(b)=P(c)=P(d)=P(e)=5 za medjusobno različite cijele brojeve a,b,c,d,e.
| Anonymous (napisa): | | Zadatak je s prijašnjih kolokvija i pise da se od p oduzme 5 pa ce sve bit jasnije?? |
Dakle promatramo polinom Q definiran ovako: Q(x)=P(x)-5.
Sada vrijedi Q(a)=Q(b)=Q(c)=Q(d)=Q(e)=0.
Treba pokazati da ne postoji cjelobrojna točka u kojoj Q ima vrijednost -5 (u toj bi točki vrijednost od P bila 0).
Mea
|
|
| [Vrh] |
|
|









