| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
DADAN KARAMBOLIS
Forumaš(ica)

Pridružen/a: 06. 02. 2006. (10:51:36)
Postovi: (7)16
|
|
| [Vrh] |
|
DADAN KARAMBOLIS
Forumaš(ica)

Pridružen/a: 06. 02. 2006. (10:51:36)
Postovi: (7)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 2:11 čet, 23. 2. 2006 Naslov: Postano: 2:11 čet, 23. 2. 2006 Naslov: |
    |
|
|
Što se tiče tog zadatka, asistentica na vježbama je rekla da je pogrešno zadan, tj. da ne stoji
[latex]\overrightarrow{OT}=\sum_{i=0}^{n}\alpha_i \overrightarrow{OA_i}[/latex]
već
[latex]\overrightarrow{OT} + \overrightarrow{OA_0}=\sum_{i=0}^{n}\alpha_i \overrightarrow{OA_i}[/latex].
To što su točke [latex]A_0, A_1, \dots , A_n[/latex] linearno nezavisne povlači da su i vektori [latex]\overrightarrow{A_0 A_1}, \overrightarrow{A_0 A_2}, \dots , \overrightarrow{A_0 A_n}[/latex] linearno nezavisni i oni čine bazu u [latex]V^n[/latex].
Tada za [latex]\overrightarrow{OT}[/latex] postoje jedinstveni koeficijenti [latex]\beta_1 , \beta_2 , \dots , \beta_n[/latex] pomoću kojih se taj vektor može na jednistven način pokazati kao zbroj vektora baze, tj. [latex]\overrightarrow{OT}=\sum_{i=1}^{n} \beta_i \overrightarrow{A_0 A_i}[/latex].
Sada malo tu sumu raspisujemo:
[latex]\overrightarrow{OT}=\sum_{i=1}^{n} \beta_i \overrightarrow{A_0 A_i} = \sum_{i=1}^{n} \beta_i (\overrightarrow{A_0 O} + \overrightarrow{O A_i})= \\
\sum_{i=1}^{n} \beta_i \overrightarrow{A_0 O} + \sum_{i=1}^{n} \beta_i \overrightarrow{O A_i} = - \sum_{i=1}^{n} \beta_i \overrightarrow{O A_0} + \sum_{i=1}^{n} \beta_i \overrightarrow{O A_i}
[/latex]
Sada uzmemo da je [latex]\beta_i = \alpha_i[/latex] za svaki i>0, a vrijedi još [latex]\sum_{i=0}^{n}\alpha_i = 1[/latex].
Sada vrijedi:
[latex]\alpha_0 = 1 - \sum_{i=1}^{n}\alpha_i = 1 - \sum_{i=1}^{n}\beta_i[/latex].
Pokažimo da to vrijedi za vektor iz zadatka, tj. pretpostavimo da vrijedi
[latex]\overrightarrow{OT} + \overrightarrow{OA_0}=\sum_{i=0}^{n}\alpha_i \overrightarrow{OA_i}[/latex].
Ako malo rastavimo ovu sumu, dobivamo:
[latex]\overrightarrow{OT} + \overrightarrow{OA_0}=\alpha_0 \overrightarrow{OA_0} + \sum_{i=1}^{n}\alpha_i \overrightarrow{OA_i}[/latex].
Možemo sada umjesto [latex]\alpha_i[/latex] uvrstiti [latex]\beta_i[/latex] za i>0, a za i=0 uvrstiti: [latex]\alpha_0 = 1 - \sum_{i=1}^{n}\alpha_i = 1 - \sum_{i=1}^{n}\beta_i[/latex].
Sada imamo:
[latex]\overrightarrow{OT} + \overrightarrow{OA_0}=(1 - \sum_{i=1}^{n}\beta_i ) \overrightarrow{OA_0} + \sum_{i=1}^{n}\beta_i \overrightarrow{OA_i}[/latex]
[latex]\overrightarrow{OT} + \overrightarrow{OA_0}=\overrightarrow{OA_0} - \sum_{i=1}^{n}\beta_i \overrightarrow{OA_0}+ \sum_{i=1}^{n}\beta_i \overrightarrow{OA_i}[/latex]
Ove dvije sume su upravo jednake [latex]\overrightarrow{OT}[/latex], pa sada imamo:
[latex]\overrightarrow{OT} + \overrightarrow{OA_0}=\overrightarrow{OT} + \overrightarrow{OA_0}[/latex], tj. tvrdnja je dokazana.
Nadam se da je sada jasnije, na vježbama smo dosta potrošili na ovaj zadatak da bi nakraju zaključili da je pogrešno zadan.
Što se tiče tog zadatka, asistentica na vježbama je rekla da je pogrešno zadan, tj. da ne stoji
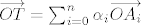
već
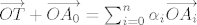 . .
To što su točke 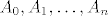 linearno nezavisne povlači da su i vektori linearno nezavisne povlači da su i vektori 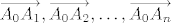 linearno nezavisni i oni čine bazu u linearno nezavisni i oni čine bazu u 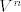 . .
Tada za 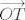 postoje jedinstveni koeficijenti postoje jedinstveni koeficijenti 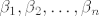 pomoću kojih se taj vektor može na jednistven način pokazati kao zbroj vektora baze, tj. pomoću kojih se taj vektor može na jednistven način pokazati kao zbroj vektora baze, tj. 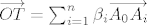 . .
Sada malo tu sumu raspisujemo:
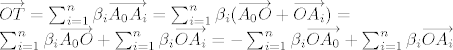
Sada uzmemo da je 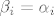 za svaki i>0, a vrijedi još za svaki i>0, a vrijedi još 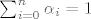 . .
Sada vrijedi:
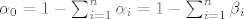 . .
Pokažimo da to vrijedi za vektor iz zadatka, tj. pretpostavimo da vrijedi
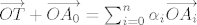 . .
Ako malo rastavimo ovu sumu, dobivamo:
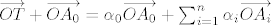 . .
Možemo sada umjesto 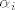 uvrstiti uvrstiti 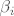 za i>0, a za i=0 uvrstiti: za i>0, a za i=0 uvrstiti: 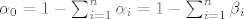 . .
Sada imamo:
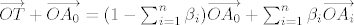
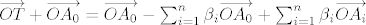
Ove dvije sume su upravo jednake 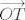 , pa sada imamo: , pa sada imamo:
 , tj. tvrdnja je dokazana. , tj. tvrdnja je dokazana.
Nadam se da je sada jasnije, na vježbama smo dosta potrošili na ovaj zadatak da bi nakraju zaključili da je pogrešno zadan.
_________________
The Dude Abides
|
|
| [Vrh] |
|
DADAN KARAMBOLIS
Forumaš(ica)

Pridružen/a: 06. 02. 2006. (10:51:36)
Postovi: (7)16
|
|
| [Vrh] |
|
DADAN KARAMBOLIS
Forumaš(ica)

Pridružen/a: 06. 02. 2006. (10:51:36)
Postovi: (7)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
vjakovac
Forumaš s poteškoćama u pisanju

Pridružen/a: 28. 02. 2006. (10:07:16)
Postovi: (4B)16
|
 Postano: 22:31 uto, 28. 2. 2006 Naslov: Postano: 22:31 uto, 28. 2. 2006 Naslov: |
    |
|
|
[quote="DADAN KARAMBOLIS"]dali je kod afinih preslikavanja dovoljno da detreminanta matrice bude razlicita od 0(cini mi se) da bi mogli zakljucit da je to bijekcija...[/quote]
Svako afino preslikavanje na [latex]\mathbb{E}^n[/latex] se može prikazati kao kompozicija nekog linearnog operatora A i translacije za neki vektor.
To preslikavanje je bijekcija ako i samo ako je [latex]\det A\neq 0[/latex]. Dakle, odgovor je potvrdan.
Dokaz te činjenice je trivijalan: translacije su bijekcije, kompozicija bijekcija je opet bijekcija, linearni operator je bijektivan akko mu je det različita od 0.
_________________
Ups, čini mi se da sam zakasnio. :)
[color=darkred][b][i]"Tko dvije, njemu prije."[/i][/b][/color]
| DADAN KARAMBOLIS (napisa): | | dali je kod afinih preslikavanja dovoljno da detreminanta matrice bude razlicita od 0(cini mi se) da bi mogli zakljucit da je to bijekcija... |
Svako afino preslikavanje na 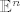 se može prikazati kao kompozicija nekog linearnog operatora A i translacije za neki vektor. se može prikazati kao kompozicija nekog linearnog operatora A i translacije za neki vektor.
To preslikavanje je bijekcija ako i samo ako je 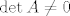 . Dakle, odgovor je potvrdan. . Dakle, odgovor je potvrdan.
Dokaz te činjenice je trivijalan: translacije su bijekcije, kompozicija bijekcija je opet bijekcija, linearni operator je bijektivan akko mu je det različita od 0.
_________________
Ups, čini mi se da sam zakasnio. 
"Tko dvije, njemu prije."
|
|
| [Vrh] |
|
|





