| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
vanish
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (22:45:35)
Postovi: (6D)16
Spol: 
Lokacija: stambena zgrada
|
|
| [Vrh] |
|
bla bla
Forumaš(ica)


Pridružen/a: 15. 02. 2006. (19:07:44)
Postovi: (41)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
marinaa
Gost
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 17:23 pon, 24. 4. 2006 Naslov: Postano: 17:23 pon, 24. 4. 2006 Naslov: |
    |
|
|
Grupa gdje je 1. zadatak (x*sin(x)-x*cos(x))^2
1. 0
2. a1=2, a2=-2
3. alfa=1 beta=pi/2, f je klase C1(R)
4. raste na <-inf,3>, pada na <3,+inf>, maksimum u 3
Grupa gdje je 1. zadatak (x*sin(x)-x*cos(x))^2
1. 0
2. a1=2, a2=-2
3. alfa=1 beta=pi/2, f je klase C1(R)
4. raste na <-inf,3>, pada na <3,+inf>, maksimum u 3
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Sasuke
Forumaš(ica)

Pridružen/a: 27. 06. 2005. (19:22:00)
Postovi: (47)16
Spol: 
Lokacija: zemlja
|
|
| [Vrh] |
|
bernard_z
Forumaš(ica)

Pridružen/a: 23. 04. 2006. (20:39:06)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
Sasuke
Forumaš(ica)

Pridružen/a: 27. 06. 2005. (19:22:00)
Postovi: (47)16
Spol: 
Lokacija: zemlja
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
bernard_z
Forumaš(ica)

Pridružen/a: 23. 04. 2006. (20:39:06)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 21:33 pon, 24. 4. 2006 Naslov: Postano: 21:33 pon, 24. 4. 2006 Naslov: |
    |
|
|
e da, tu sam rijec trazio, stota derivacija ubije ovaj prvi clan, a ovaj drugi prezivi, al onda stota derivacija u nuli pobije sve zivo i ostane samo 0 :lol:
(nesto tipa ide funkcija f(x)=(x*sin(x)-x*cos(x))^2 ulicom, ali naleti zlocesti linearni operator deriviranja i kaze joj derivirat cu te 100 puta, funkcija mu hladno odvrati pa sta onda, a operator joj kaze... :lol: i tako dalje, mozete si sami nastavit pricu ako vas zabavlja kao, recimo, mene)
e da, tu sam rijec trazio, stota derivacija ubije ovaj prvi clan, a ovaj drugi prezivi, al onda stota derivacija u nuli pobije sve zivo i ostane samo 0 
(nesto tipa ide funkcija f(x)=(x*sin(x)-x*cos(x))^2 ulicom, ali naleti zlocesti linearni operator deriviranja i kaze joj derivirat cu te 100 puta, funkcija mu hladno odvrati pa sta onda, a operator joj kaze...  i tako dalje, mozete si sami nastavit pricu ako vas zabavlja kao, recimo, mene) i tako dalje, mozete si sami nastavit pricu ako vas zabavlja kao, recimo, mene)
|
|
| [Vrh] |
|
ana345
Forumaš(ica)

Pridružen/a: 24. 04. 2006. (21:12:55)
Postovi: (3)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 22:39 pon, 24. 4. 2006 Naslov: Postano: 22:39 pon, 24. 4. 2006 Naslov: |
    |
|
|
[quote="ana345"]
Ja sam isto tako dobila, funkcija je x^2sin2x je neparna pa je njena parna derivacija u 0= 0. :)[/quote]
Ne kuzim vezu, jel mislis ako je f neparna i ima parnu derivaciju u 0, onda je ta parna derivacija nuzno jednaka 0?
Jer npr. funkcija 1/x je neparna ali nije ni definirana u 0, a nema ni derivaciju, a treći korijen iz x je definirana u 0, ali nema derivaciju.
E, sad, kako vidjeti (bez Leibniza) da funkcija ima stotu derivaciju u 0? :cry:
Toliko pitanja, a tako malo vremena
| ana345 (napisa): |
Ja sam isto tako dobila, funkcija je x^2sin2x je neparna pa je njena parna derivacija u 0= 0.  |
Ne kuzim vezu, jel mislis ako je f neparna i ima parnu derivaciju u 0, onda je ta parna derivacija nuzno jednaka 0?
Jer npr. funkcija 1/x je neparna ali nije ni definirana u 0, a nema ni derivaciju, a treći korijen iz x je definirana u 0, ali nema derivaciju.
E, sad, kako vidjeti (bez Leibniza) da funkcija ima stotu derivaciju u 0? 
Toliko pitanja, a tako malo vremena
Zadnja promjena: alen; 22:59 pon, 24. 4. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 23:05 pon, 24. 4. 2006 Naslov: Postano: 23:05 pon, 24. 4. 2006 Naslov: |
    |
|
|
[quote="alen"][quote="ana345"]
Ja sam isto tako dobila, funkcija je x^2sin2x je neparna pa je njena parna derivacija u 0= 0. :)[/quote]
Ne kuzim vezu, jel mislis ako je f neparna i ima parnu derivaciju u 0, onda je ta parna derivacija nuzno jednaka 0?
Jer npr. funkcija 1/x je neparna ali nije ni definirana u 0, a nema ni derivaciju, a treći korijen iz x je definirana u 0, ali nema derivaciju[/quote]
Ima smisla to što je rekla, recimo uz (grubu) pretpostavku na [latex]f[/latex] da je definirana na nekom simetričnom otvorenom intervalu [latex]I[/latex] oko nule, da je parna/neparna i da je klase [latex]C^{\infty}(I)[/latex], onda je svaka neparna/parna derivacija u 0 jednaka 0.
Npr. ako je f parna onda je za sve [latex]x \in I[/latex]
[latex]f'(-x):=\lim_{h \rightarrow 0} \frac{f(-x+h)-f(-x)}{h}=\lim_{h \rightarrow 0} \frac{f(-x-h)-f(-x)}{-h}=[/latex][latex]-\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}=-f'(x)[/latex],
tj. njena derivacija je neparna funkcija na [latex]I[/latex], pa je svakako [latex]f'(0)=-f'(0)[/latex], tj. [latex]f'(0)=0[/latex].
Analogno dokažeš da je (uz iste pretpostavke) derivacija neparne funkcije, parna funkcija, pa iz toga slijedi ovo gore što sam napisao.
| alen (napisa): | | ana345 (napisa): |
Ja sam isto tako dobila, funkcija je x^2sin2x je neparna pa je njena parna derivacija u 0= 0.  |
Ne kuzim vezu, jel mislis ako je f neparna i ima parnu derivaciju u 0, onda je ta parna derivacija nuzno jednaka 0?
Jer npr. funkcija 1/x je neparna ali nije ni definirana u 0, a nema ni derivaciju, a treći korijen iz x je definirana u 0, ali nema derivaciju |
Ima smisla to što je rekla, recimo uz (grubu) pretpostavku na  da je definirana na nekom simetričnom otvorenom intervalu da je definirana na nekom simetričnom otvorenom intervalu 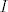 oko nule, da je parna/neparna i da je klase oko nule, da je parna/neparna i da je klase 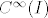 , onda je svaka neparna/parna derivacija u 0 jednaka 0. , onda je svaka neparna/parna derivacija u 0 jednaka 0.
Npr. ako je f parna onda je za sve 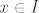
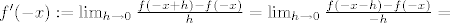 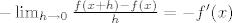 , ,
tj. njena derivacija je neparna funkcija na 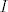 , pa je svakako , pa je svakako 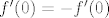 , tj. , tj. 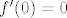 . .
Analogno dokažeš da je (uz iste pretpostavke) derivacija neparne funkcije, parna funkcija, pa iz toga slijedi ovo gore što sam napisao.
Zadnja promjena: Ilja; 23:11 pon, 24. 4. 2006; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
|












