| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 17:44 ned, 23. 7. 2006 Naslov: Malo (ne)potrebnog filozofiranja o izjavama iliti sudovima Postano: 17:44 ned, 23. 7. 2006 Naslov: Malo (ne)potrebnog filozofiranja o izjavama iliti sudovima |
    |
|
|
Naslov donekle opisuje o čemu ću pisati. Odmah molim one, kojima će se ovo činiti kao nepotrebno cjepidlačenje i mlaćenje prazne slame, neka mi ne zamjere zbog toga. Naime, imam nekoliko nedoumica što se tiču izjava (sudova) u matematičkoj logici, ali i općenito matematičkih definicija.
Krećem od "definicije" (možda je to više izjava, he he, mala igra riječi) izjave ili suda iz knjige "Elementarna matematika 1" koja kaže, citiram '[b]Izjava [/b]ili [b]sud[/b] je smislena rečenica koja može biti [b]istinita [/b]ili [b]lažna[/b] (neistinita).' Je li smisao te rečenice 'Izjava je smislena rečenica.', a ona pak može biti istinita ili lažna? Ili to znači da je izjava svaka smislena rečenica koja je istinita ili lažna, tj. da je ta istinitost u stvari određuje? Najvjerojatnije (99.9%) je da je ovo drugo. Međutim, dalje kaže 'Od izjava možemo tvoriti nove složene izjave povezujući polazne izjave veznicima, odnosno negirajući ih.' Dalje "definira" (stavljam navodnike jer nigdje ne piše da je to definicija nego se samo navodi) '[b]Konjunkcija[/b] A&B dvaju izjava A i B je složena izjava nastala povezivanjem izjava A, B veznikom [b]i[/b] za koji se upotrebljava simbol &. (…) Izjava A&B je po definiciji točna ako su izjave A, B istinite.', ali '[b]Disjunkcija[/b] A[latex]\land[/latex]B dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.'. Implikacija i ekvivalencija su definirane na isti način kao disjunkcija. Koje je sad ispravno? Mislim, jesu li te izjave definirane preko povezivanja dviju izjava veznicima ili preko istinitosti? Međutim opet, kad bi bile definirane preko istinitosti, otkud nam te dvije izjave koje se spominju ako ih prethodno nismo povezali veznikom ili nešto drugo s njima napravili? A ako možemo odrediti istinitost složenih izjava, to znači da su i one izjave. Znači li to da se tu može govoriti i o nekoj grupi izjava ili nečemu takvom?
Još da malo dotaknem i ovo o negiranju izjava. Kad imamo neku izjavu i negiramo negaciju te izjave, jesu li te izjave iste ili samo imaju iste vrijednosti istinitosti ili je to u stvari isto?
Uglavnom, nije mi jasno otkud takva nepreciznost i nonšalancija u matematičkim knjigama? :shock: Mislim, ovo je nevažan primjer i ne utječe puno, ali i mnoge važnije stvari su tako napisane. Ne razumijem, kako to da u matematici ne postoje točne definicije i teoremi kojih bi se svi pridržavali? Ako bi nešto trebalo biti uređeno, to je matematika. :?
P.S. Znam da svi imaju pametnijeg posla, nego čitati ovakve tekstove, ali ipak…
Naslov donekle opisuje o čemu ću pisati. Odmah molim one, kojima će se ovo činiti kao nepotrebno cjepidlačenje i mlaćenje prazne slame, neka mi ne zamjere zbog toga. Naime, imam nekoliko nedoumica što se tiču izjava (sudova) u matematičkoj logici, ali i općenito matematičkih definicija.
Krećem od "definicije" (možda je to više izjava, he he, mala igra riječi) izjave ili suda iz knjige "Elementarna matematika 1" koja kaže, citiram 'Izjava ili sud je smislena rečenica koja može biti istinita ili lažna (neistinita).' Je li smisao te rečenice 'Izjava je smislena rečenica.', a ona pak može biti istinita ili lažna? Ili to znači da je izjava svaka smislena rečenica koja je istinita ili lažna, tj. da je ta istinitost u stvari određuje? Najvjerojatnije (99.9%) je da je ovo drugo. Međutim, dalje kaže 'Od izjava možemo tvoriti nove složene izjave povezujući polazne izjave veznicima, odnosno negirajući ih.' Dalje "definira" (stavljam navodnike jer nigdje ne piše da je to definicija nego se samo navodi) 'Konjunkcija A&B dvaju izjava A i B je složena izjava nastala povezivanjem izjava A, B veznikom i za koji se upotrebljava simbol &. (…) Izjava A&B je po definiciji točna ako su izjave A, B istinite.', ali 'Disjunkcija A B dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.'. Implikacija i ekvivalencija su definirane na isti način kao disjunkcija. Koje je sad ispravno? Mislim, jesu li te izjave definirane preko povezivanja dviju izjava veznicima ili preko istinitosti? Međutim opet, kad bi bile definirane preko istinitosti, otkud nam te dvije izjave koje se spominju ako ih prethodno nismo povezali veznikom ili nešto drugo s njima napravili? A ako možemo odrediti istinitost složenih izjava, to znači da su i one izjave. Znači li to da se tu može govoriti i o nekoj grupi izjava ili nečemu takvom? B dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.'. Implikacija i ekvivalencija su definirane na isti način kao disjunkcija. Koje je sad ispravno? Mislim, jesu li te izjave definirane preko povezivanja dviju izjava veznicima ili preko istinitosti? Međutim opet, kad bi bile definirane preko istinitosti, otkud nam te dvije izjave koje se spominju ako ih prethodno nismo povezali veznikom ili nešto drugo s njima napravili? A ako možemo odrediti istinitost složenih izjava, to znači da su i one izjave. Znači li to da se tu može govoriti i o nekoj grupi izjava ili nečemu takvom?
Još da malo dotaknem i ovo o negiranju izjava. Kad imamo neku izjavu i negiramo negaciju te izjave, jesu li te izjave iste ili samo imaju iste vrijednosti istinitosti ili je to u stvari isto?
Uglavnom, nije mi jasno otkud takva nepreciznost i nonšalancija u matematičkim knjigama?  Mislim, ovo je nevažan primjer i ne utječe puno, ali i mnoge važnije stvari su tako napisane. Ne razumijem, kako to da u matematici ne postoje točne definicije i teoremi kojih bi se svi pridržavali? Ako bi nešto trebalo biti uređeno, to je matematika. Mislim, ovo je nevažan primjer i ne utječe puno, ali i mnoge važnije stvari su tako napisane. Ne razumijem, kako to da u matematici ne postoje točne definicije i teoremi kojih bi se svi pridržavali? Ako bi nešto trebalo biti uređeno, to je matematika. 
P.S. Znam da svi imaju pametnijeg posla, nego čitati ovakve tekstove, ali ipak…
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:11 ned, 23. 7. 2006 Naslov: Re: Malo (ne)potrebnog filozofiranja o izjavama iliti sudovi Postano: 22:11 ned, 23. 7. 2006 Naslov: Re: Malo (ne)potrebnog filozofiranja o izjavama iliti sudovi |
    |
|
|
[quote="Silver Surfer"]Uglavnom, nije mi jasno otkud takva nepreciznost i nonšalancija u matematičkim knjigama? :shock: Mislim, ovo je nevažan primjer i ne utječe puno, ali i mnoge važnije stvari su tako napisane. Ne razumijem, kako to da u matematici ne postoje točne definicije i teoremi kojih bi se svi pridržavali? Ako bi nešto trebalo biti uređeno, to je matematika. :?[/quote]
Sto je skup? :-k
Kratko: da bi mogao precizno nesto definirati, trebaju ti pojmovi pomocu kojih ces definirati novi pojam. :-s No, kako definirati prvi pojam u nekoj teoriji, dok jos nemas drugih pojmova koje bi mogao iskoristiti? :-k Tu je potrebno biti deskriptivan i osloniti se na "zdravi razum". :(
Da, izjava je izjava bas zato jer je moguce utvrditi njenu istinitost. 8)
| Silver Surfer (napisa): | Uglavnom, nije mi jasno otkud takva nepreciznost i nonšalancija u matematičkim knjigama?  Mislim, ovo je nevažan primjer i ne utječe puno, ali i mnoge važnije stvari su tako napisane. Ne razumijem, kako to da u matematici ne postoje točne definicije i teoremi kojih bi se svi pridržavali? Ako bi nešto trebalo biti uređeno, to je matematika. Mislim, ovo je nevažan primjer i ne utječe puno, ali i mnoge važnije stvari su tako napisane. Ne razumijem, kako to da u matematici ne postoje točne definicije i teoremi kojih bi se svi pridržavali? Ako bi nešto trebalo biti uređeno, to je matematika.  |
Sto je skup? 
Kratko: da bi mogao precizno nesto definirati, trebaju ti pojmovi pomocu kojih ces definirati novi pojam.  No, kako definirati prvi pojam u nekoj teoriji, dok jos nemas drugih pojmova koje bi mogao iskoristiti? No, kako definirati prvi pojam u nekoj teoriji, dok jos nemas drugih pojmova koje bi mogao iskoristiti?  Tu je potrebno biti deskriptivan i osloniti se na "zdravi razum". Tu je potrebno biti deskriptivan i osloniti se na "zdravi razum". 
Da, izjava je izjava bas zato jer je moguce utvrditi njenu istinitost. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:32 ned, 23. 7. 2006 Naslov: Postano: 22:32 ned, 23. 7. 2006 Naslov: |
    |
|
|
[quote="Silver Surfer"]Znam, naravno da neke pojmove ne možeš definirati. Međutim, svatko intuitivno zna što je skup, ali ne zna što je konjunkcija.[/quote]
Citiram tvoj prijepis definicije konjukcije (ne ulazim u to da li u knjizi pise "definicija"):
[quote="Silver Surfer"]'Konjunkcija A&B dvaju izjava A i B je složena izjava nastala povezivanjem izjava A, B veznikom i za koji se upotrebljava simbol &. (…) Izjava A&B je po definiciji točna ako su izjave A, B istinite.'[/quote]
Ovime se definira konjukcija na slijedeci nacin:
1. "[b]Konjunkcija[/b] [color=#aaaaaa]A&B dvaju izjava A i B[/color] [b]je[/b] [color=#aaaaaa]složena[/color] [b]izjava[/b]..." :arrow: Dakle, konjukcija je izjava, sto znaci "recenica kojoj je moguce odrediti istinitost" 8)
2. "Izjava A&B je po [u]definiciji[/u] točna ako su izjave A, B istinite" :arrow: Dakle, [u]definiramo[/u] vrijednost izjave A&B kao istinu ako je A istina i ako je B istina; inace je vrijednost izjave A&B laz (jer trece mogucnosti nema). 8)
Dakle, ne trazi se da intuitivno znas sto je konjukcija (dapace, nju ovime definiras), nego da znas sto znaci da "su izjave A, B istinite". :D
| Silver Surfer (napisa): | | Znam, naravno da neke pojmove ne možeš definirati. Međutim, svatko intuitivno zna što je skup, ali ne zna što je konjunkcija. |
Citiram tvoj prijepis definicije konjukcije (ne ulazim u to da li u knjizi pise "definicija"):
| Silver Surfer (napisa): | | 'Konjunkcija A&B dvaju izjava A i B je složena izjava nastala povezivanjem izjava A, B veznikom i za koji se upotrebljava simbol &. (…) Izjava A&B je po definiciji točna ako su izjave A, B istinite.' |
Ovime se definira konjukcija na slijedeci nacin:
1. "Konjunkcija A&B dvaju izjava A i B je složena izjava..."  Dakle, konjukcija je izjava, sto znaci "recenica kojoj je moguce odrediti istinitost" Dakle, konjukcija je izjava, sto znaci "recenica kojoj je moguce odrediti istinitost" 
2. "Izjava A&B je po definiciji točna ako su izjave A, B istinite"  Dakle, definiramo vrijednost izjave A&B kao istinu ako je A istina i ako je B istina; inace je vrijednost izjave A&B laz (jer trece mogucnosti nema). Dakle, definiramo vrijednost izjave A&B kao istinu ako je A istina i ako je B istina; inace je vrijednost izjave A&B laz (jer trece mogucnosti nema). 
Dakle, ne trazi se da intuitivno znas sto je konjukcija (dapace, nju ovime definiras), nego da znas sto znaci da "su izjave A, B istinite". 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:49 ned, 23. 7. 2006 Naslov: Postano: 22:49 ned, 23. 7. 2006 Naslov: |
    |
|
|
Kako drugacije? :grebgreb:
[quote="Silver Surfer"]Disjunkcija [latex]A \land B[/latex] dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.'[/quote]
Za pocetak, krivi simbol si stavio:
[quote="Silver Surfer"]Disjunkcija [latex]A \lor B[/latex] dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.'[/quote]
Kod konjukcije smo rekli kad je istina, a kod disjunkcije kad je laz. :| Nije bas neka duboka razlika u pristupu... ;)
Kako drugacije? 
| Silver Surfer (napisa): | Disjunkcija 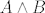 dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.' dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.' |
Za pocetak, krivi simbol si stavio:
| Silver Surfer (napisa): | Disjunkcija 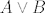 dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.' dviju izjava A, B je složena izjava koja je lažna točno onda ako su obje izjave A, B lažne.' |
Kod konjukcije smo rekli kad je istina, a kod disjunkcije kad je laz.  Nije bas neka duboka razlika u pristupu... Nije bas neka duboka razlika u pristupu... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 23:10 ned, 23. 7. 2006 Naslov: Postano: 23:10 ned, 23. 7. 2006 Naslov: |
    |
|
|
[quote="Silver Surfer"]Pa samo je rečeno za istinitost, a nije rečeno da je nastala povezivanjem izjava veznikom ili, recimo.[/quote]
Stvar simbola; ne mislim da je to jako bitno za naglasiti kad ti vec pise simbol. 8)
[quote="Silver Surfer"]Je li svaka izjava koja je lazna kada su i A i B lažne isto disjunkcija?[/quote]
Ako je laz tada i samo tada, onda je ona ekvivalentna disjunkciji. 8)
No, ne mozes reci da je [latex]\neg(\neg A \land \neg B)[/latex] disjunkcija, ne? ;) Zato i sluzi ono [latex]A \lor B[/latex] - da znas kojeg je oblika disjunkcija. 8)
| Silver Surfer (napisa): | | Pa samo je rečeno za istinitost, a nije rečeno da je nastala povezivanjem izjava veznikom ili, recimo. |
Stvar simbola; ne mislim da je to jako bitno za naglasiti kad ti vec pise simbol. 
| Silver Surfer (napisa): | | Je li svaka izjava koja je lazna kada su i A i B lažne isto disjunkcija? |
Ako je laz tada i samo tada, onda je ona ekvivalentna disjunkciji. 
No, ne mozes reci da je 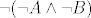 disjunkcija, ne? disjunkcija, ne?  Zato i sluzi ono Zato i sluzi ono 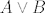 - da znas kojeg je oblika disjunkcija. - da znas kojeg je oblika disjunkcija. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 23:31 ned, 23. 7. 2006 Naslov: Postano: 23:31 ned, 23. 7. 2006 Naslov: |
    |
|
|
Ne, jer nije oblika [latex]A \lor B[/latex] (dakle "[tt]A znak_operatora B[/tt]"). :ccc: Sjeti se normalnih formi sa UuRa - tocno se zna kako moraju izgledati; sve ostalo spada pod "sredjivanje" izraza. 8)
Ako ti napises "[tt]A + B[/tt]" je laz ako i samo ako su i A i B laz, onda to [b]JE[/b] disjunkcija, samo sto si odabrao drugi simbol za nju. 8) Slucajno, "+" se i inace koristi za disjunkciju, no mogao si staviti kakav god simbol... :)
Ono gore nije disjunkcija nego negacija konjukcije negacija izjava A i B. 8)
Recimo, dva "medvjeda" (kovanice od 5kn) imaju [b]istu vrijednost[/b] kao novcanica od 10kn, ali dvije kovanice od 5kn [b]nisu[/b] novcanica od 10kn. :) Jasnije? :D
Ne, jer nije oblika 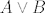 (dakle "A znak_operatora B"). (dakle "A znak_operatora B").  Sjeti se normalnih formi sa UuRa - tocno se zna kako moraju izgledati; sve ostalo spada pod "sredjivanje" izraza. Sjeti se normalnih formi sa UuRa - tocno se zna kako moraju izgledati; sve ostalo spada pod "sredjivanje" izraza. 
Ako ti napises "A + B" je laz ako i samo ako su i A i B laz, onda to JE disjunkcija, samo sto si odabrao drugi simbol za nju.  Slucajno, "+" se i inace koristi za disjunkciju, no mogao si staviti kakav god simbol... Slucajno, "+" se i inace koristi za disjunkciju, no mogao si staviti kakav god simbol... 
Ono gore nije disjunkcija nego negacija konjukcije negacija izjava A i B. 
Recimo, dva "medvjeda" (kovanice od 5kn) imaju istu vrijednost kao novcanica od 10kn, ali dvije kovanice od 5kn nisu novcanica od 10kn.  Jasnije? Jasnije? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 23:51 ned, 23. 7. 2006 Naslov: Postano: 23:51 ned, 23. 7. 2006 Naslov: |
    |
|
|
Pa, to pise simbolicki. :| Ok, ne pise rijecima kako si ti naveo, ali imas simboliku: [tt]A znak_disjunkcije B[/tt]. :)
U definiciji derivacije imas [tt]f'(x)[/tt] gdje je [tt]f[/tt] nekakva funkcija. :-s Ako ja napisem negdje "[tt]f(x')[/tt]" tebi nece pasti na pamet da je to derivacija, iako imas i [tt]f[/tt] i znak koji se pojavljuje u definiciji derivacije [tt]'[/tt] i varijablu [tt]x[/tt]. :-s Zasto? Jednostavno zato jer nisu slozeni na nacin na koji to pise u definiciji: [tt]f'(x)[/tt]. :g:
Ista stvar je i ovdje: ako nije oblika [tt]A operator B[/tt], nije disjunkcija jer tako pise u definiciji. :) Da moze biti bilo kojeg oblika, pisalo bi "izjava koja sadrzi samo izjave A i B i logicke operatore". 8)
Pa, to pise simbolicki.  Ok, ne pise rijecima kako si ti naveo, ali imas simboliku: A znak_disjunkcije B. Ok, ne pise rijecima kako si ti naveo, ali imas simboliku: A znak_disjunkcije B. 
U definiciji derivacije imas f'(x) gdje je f nekakva funkcija.  Ako ja napisem negdje "f(x')" tebi nece pasti na pamet da je to derivacija, iako imas i f i znak koji se pojavljuje u definiciji derivacije ' i varijablu x. Ako ja napisem negdje "f(x')" tebi nece pasti na pamet da je to derivacija, iako imas i f i znak koji se pojavljuje u definiciji derivacije ' i varijablu x.  Zasto? Jednostavno zato jer nisu slozeni na nacin na koji to pise u definiciji: f'(x). Zasto? Jednostavno zato jer nisu slozeni na nacin na koji to pise u definiciji: f'(x). 
Ista stvar je i ovdje: ako nije oblika A operator B, nije disjunkcija jer tako pise u definiciji.  Da moze biti bilo kojeg oblika, pisalo bi "izjava koja sadrzi samo izjave A i B i logicke operatore". Da moze biti bilo kojeg oblika, pisalo bi "izjava koja sadrzi samo izjave A i B i logicke operatore". 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 0:04 pon, 24. 7. 2006 Naslov: Postano: 0:04 pon, 24. 7. 2006 Naslov: |
    |
|
|
Znači, želiš reći da se konjunkcija, disjunkcija, implikacija i ekvivalencija razlikuju samo po tablicama istinitosti jer su sve oblika A operator B? Je li to znači da to nema veze sa jezičnim oblikom, A i B, A ili B, ako A onda B,...? To je kao da si lakše predočimo, ili tako nešto?
Znači, želiš reći da se konjunkcija, disjunkcija, implikacija i ekvivalencija razlikuju samo po tablicama istinitosti jer su sve oblika A operator B? Je li to znači da to nema veze sa jezičnim oblikom, A i B, A ili B, ako A onda B,...? To je kao da si lakše predočimo, ili tako nešto?
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 0:12 pon, 24. 7. 2006 Naslov: Postano: 0:12 pon, 24. 7. 2006 Naslov: |
    |
|
|
[quote="Silver Surfer"]Znači, želiš reći da se konjunkcija, disjunkcija, implikacija i ekvivalencija razlikuju samo po tablicama istinitosti jer su sve oblika A operator B?[/quote]
Tocno tako. 8) Naravno, bilo bi neprakticno izmisljati svoje oznake za te operatore, ali - formalno - nitko ti ne brani; samo moras napisati "Neka [tt]tvoja oznaka[/tt] oznacava konjukciju" i sve je ok! :D
[quote="Silver Surfer"]Je li to znači da to nema veze sa jezičnim oblikom, A i B, A ili B, ako A onda B,...? To je kao da si lakše predočimo, ili tako nešto?[/quote]
Pa, ne da si lakse predocimo, nego da znamo oznaciti (i procitati). 8) Kao sto "[tt]+[/tt]" oznacava zbrajanje: iako se ne bi nista promijenilo da upotrijebimo "[tt]?[/tt]" (uz propisno naglasavanje), standardna oznaka smanjuje mogucnost zabune. 8)
Zamisli zadatak: "Ako s '[tt]+[/tt]' oznacimo mnozenje, a sa '[tt]*[/tt]' zbrajanje, izracunajte [tt]1*2+3*4+(5*6+7)[/tt]". :shock: To bi vjerojatno rijesio tako da bi si prvo "preveo" na "standardni jezik" ([tt]1+2*3+4*(5+6*7)[/tt]), pa bi tek onda isao racunati. 8) A ovo je samo jednostavan primjer... :scared:
| Silver Surfer (napisa): | | Znači, želiš reći da se konjunkcija, disjunkcija, implikacija i ekvivalencija razlikuju samo po tablicama istinitosti jer su sve oblika A operator B? |
Tocno tako.  Naravno, bilo bi neprakticno izmisljati svoje oznake za te operatore, ali - formalno - nitko ti ne brani; samo moras napisati "Neka tvoja oznaka oznacava konjukciju" i sve je ok! Naravno, bilo bi neprakticno izmisljati svoje oznake za te operatore, ali - formalno - nitko ti ne brani; samo moras napisati "Neka tvoja oznaka oznacava konjukciju" i sve je ok! 
| Silver Surfer (napisa): | | Je li to znači da to nema veze sa jezičnim oblikom, A i B, A ili B, ako A onda B,...? To je kao da si lakše predočimo, ili tako nešto? |
Pa, ne da si lakse predocimo, nego da znamo oznaciti (i procitati).  Kao sto "+" oznacava zbrajanje: iako se ne bi nista promijenilo da upotrijebimo "?" (uz propisno naglasavanje), standardna oznaka smanjuje mogucnost zabune. Kao sto "+" oznacava zbrajanje: iako se ne bi nista promijenilo da upotrijebimo "?" (uz propisno naglasavanje), standardna oznaka smanjuje mogucnost zabune. 
Zamisli zadatak: "Ako s '+' oznacimo mnozenje, a sa '*' zbrajanje, izracunajte 1*2+3*4+(5*6+7)".  To bi vjerojatno rijesio tako da bi si prvo "preveo" na "standardni jezik" (1+2*3+4*(5+6*7)), pa bi tek onda isao racunati. To bi vjerojatno rijesio tako da bi si prvo "preveo" na "standardni jezik" (1+2*3+4*(5+6*7)), pa bi tek onda isao racunati.  A ovo je samo jednostavan primjer... A ovo je samo jednostavan primjer... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 7:06 pon, 24. 7. 2006 Naslov: Postano: 7:06 pon, 24. 7. 2006 Naslov: |
    |
|
|
Niz je prilicno standardan pojam, nisam primijetio puno varijacija (OK kad dodjes do Laurentovih redova domena ce postati [b]Z[/b] umjesto [b]N[/b], ali to je sitnica). Za konjukciju itd. u ozbiljnim knjigama neces naci definiciju nego samo aksiome. To je u logici nedefiniran pojam, isto kao unija i presjek u teoriji skupova. Na Elementarnoj glumimo definicije - to se zove naivna teorija skupova, odn. logika. Te "definicije" su zapravo objasnjenja mahanjem rukama, pa ih je malo teze standardizirati.
Niz je prilicno standardan pojam, nisam primijetio puno varijacija (OK kad dodjes do Laurentovih redova domena ce postati Z umjesto N, ali to je sitnica). Za konjukciju itd. u ozbiljnim knjigama neces naci definiciju nego samo aksiome. To je u logici nedefiniran pojam, isto kao unija i presjek u teoriji skupova. Na Elementarnoj glumimo definicije - to se zove naivna teorija skupova, odn. logika. Te "definicije" su zapravo objasnjenja mahanjem rukama, pa ih je malo teze standardizirati.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 20:09 uto, 1. 8. 2006 Naslov: Postano: 20:09 uto, 1. 8. 2006 Naslov: |
    |
|
|
Evo mene opet! :D Naime, sad kad sam ponovno pročitao sve što smo napisali, sve mi je puno jasnije. Zbog toga zahvaljujem vsegi i krcku na objašnjenjima. I mislim da bi to sve trebalo pisati u knjizi da ljudima bude jasnije, jer iz onih par rečenica se to ne da vidjeti.
Međutim, ne bih ja bio Silver Surfer kad mi nešto ne bi bilo jasno.
Prvo, ne razumijem zašto kod onoga "Izjava A&B je po definiciji točna ako (i zašto u ovakvim stvarima ne piše ako i amo ako?) su izjave A, B istinite." piše točna, a ne istinita kad se cijelo vrijeme koristi istinita i lažna. Netko bi možda za "točna" mogao pomisliti u smislu ispravno oblikovana konjunkcija.
Drugo, mislim da definicija, recimo, konjunkcije nije dobra kao "AoperatorB i njezina tablica istinitosti", a da to slučajno čitamo A i B, jer na primjer izjava "Pada kiša i dan je." je stvarno istinita baš kada i pada kiša i dan je. Znači li to da operator može biti bilo koji znak, ali konjunkciju uvijek moramo čitati A i B i taj operator označava veznik "i"? Malo sam zakomplicirao i vrtim se u krug, ali nadam se da se vidi što mi točno nije jasno.
Evo mene opet!  Naime, sad kad sam ponovno pročitao sve što smo napisali, sve mi je puno jasnije. Zbog toga zahvaljujem vsegi i krcku na objašnjenjima. I mislim da bi to sve trebalo pisati u knjizi da ljudima bude jasnije, jer iz onih par rečenica se to ne da vidjeti. Naime, sad kad sam ponovno pročitao sve što smo napisali, sve mi je puno jasnije. Zbog toga zahvaljujem vsegi i krcku na objašnjenjima. I mislim da bi to sve trebalo pisati u knjizi da ljudima bude jasnije, jer iz onih par rečenica se to ne da vidjeti.
Međutim, ne bih ja bio Silver Surfer kad mi nešto ne bi bilo jasno.
Prvo, ne razumijem zašto kod onoga "Izjava A&B je po definiciji točna ako (i zašto u ovakvim stvarima ne piše ako i amo ako?) su izjave A, B istinite." piše točna, a ne istinita kad se cijelo vrijeme koristi istinita i lažna. Netko bi možda za "točna" mogao pomisliti u smislu ispravno oblikovana konjunkcija.
Drugo, mislim da definicija, recimo, konjunkcije nije dobra kao "AoperatorB i njezina tablica istinitosti", a da to slučajno čitamo A i B, jer na primjer izjava "Pada kiša i dan je." je stvarno istinita baš kada i pada kiša i dan je. Znači li to da operator može biti bilo koji znak, ali konjunkciju uvijek moramo čitati A i B i taj operator označava veznik "i"? Malo sam zakomplicirao i vrtim se u krug, ali nadam se da se vidi što mi točno nije jasno.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:31 uto, 1. 8. 2006 Naslov: Postano: 20:31 uto, 1. 8. 2006 Naslov: |
    |
|
|
[quote="Silver Surfer"]Međutim, ne bih ja bio Silver Surfer kad mi nešto ne bi bilo jasno.[/quote]
Ako ce to rijesiti problem, mogu ti promijeniti nick. :D
[quote="Silver Surfer"]Prvo, ne razumijem zašto kod onoga "Izjava A&B je po definiciji točna ako (i zašto u ovakvim stvarima ne piše ako i amo ako?) su izjave A, B istinite." piše točna, a ne istinita kad se cijelo vrijeme koristi istinita i lažna. Netko bi možda za "točna" mogao pomisliti u smislu ispravno oblikovana konjunkcija.[/quote]
Tu se slazem da bi "istinita" bio sretniji izraz, no to je do autora knjige. 8)
Sto se tice "ako i samo ako"... cemu? :-k Recimo "broj je paran ako je djeljiv s dva" :arrow: kad kazem "paran broj, rekao sam da je on djeljiv s dva" i to je sve sto ja od definicije hocu! :D
[quote="Silver Surfer"]Drugo, mislim da definicija, recimo, konjunkcije nije dobra kao "AoperatorB i njezina tablica istinitosti", a da to slučajno čitamo A i B, jer na primjer izjava "Pada kiša i dan je." je stvarno istinita baš kada i pada kiša i dan je. Znači li to da operator može biti bilo koji znak, ali konjunkciju uvijek moramo čitati A i B i taj operator označava veznik "i"? Malo sam zakomplicirao i vrtim se u krug, ali nadam se da se vidi što mi točno nije jasno.[/quote]
Zasto ja ne bih mogao reci "A ping-pong B je logicki operator sa slijedecom tablicom istinitosti: [tt]tablica konjukcije[/tt]" i onda reci "pada kisa ping-pong dan je"? :-k To ce opet znaciti da vani pada kisa i da je dan, zar ne? :D
Besides, netko s engleskog govornog podrucja ce reci "it is raining [b]AND[/b] it is day", tj. koristit ce "and", a ne "i". 8) Matematika ne robuje jeziku; that's the part of the beauty in it! :gg:
| Silver Surfer (napisa): | | Međutim, ne bih ja bio Silver Surfer kad mi nešto ne bi bilo jasno. |
Ako ce to rijesiti problem, mogu ti promijeniti nick. 
| Silver Surfer (napisa): | | Prvo, ne razumijem zašto kod onoga "Izjava A&B je po definiciji točna ako (i zašto u ovakvim stvarima ne piše ako i amo ako?) su izjave A, B istinite." piše točna, a ne istinita kad se cijelo vrijeme koristi istinita i lažna. Netko bi možda za "točna" mogao pomisliti u smislu ispravno oblikovana konjunkcija. |
Tu se slazem da bi "istinita" bio sretniji izraz, no to je do autora knjige. 
Sto se tice "ako i samo ako"... cemu?  Recimo "broj je paran ako je djeljiv s dva" Recimo "broj je paran ako je djeljiv s dva"  kad kazem "paran broj, rekao sam da je on djeljiv s dva" i to je sve sto ja od definicije hocu! kad kazem "paran broj, rekao sam da je on djeljiv s dva" i to je sve sto ja od definicije hocu! 
| Silver Surfer (napisa): | | Drugo, mislim da definicija, recimo, konjunkcije nije dobra kao "AoperatorB i njezina tablica istinitosti", a da to slučajno čitamo A i B, jer na primjer izjava "Pada kiša i dan je." je stvarno istinita baš kada i pada kiša i dan je. Znači li to da operator može biti bilo koji znak, ali konjunkciju uvijek moramo čitati A i B i taj operator označava veznik "i"? Malo sam zakomplicirao i vrtim se u krug, ali nadam se da se vidi što mi točno nije jasno. |
Zasto ja ne bih mogao reci "A ping-pong B je logicki operator sa slijedecom tablicom istinitosti: tablica konjukcije" i onda reci "pada kisa ping-pong dan je"?  To ce opet znaciti da vani pada kisa i da je dan, zar ne? To ce opet znaciti da vani pada kisa i da je dan, zar ne? 
Besides, netko s engleskog govornog podrucja ce reci "it is raining AND it is day", tj. koristit ce "and", a ne "i".  Matematika ne robuje jeziku; that's the part of the beauty in it! Matematika ne robuje jeziku; that's the part of the beauty in it! 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Silver Surfer
Forumaš(ica)


Pridružen/a: 09. 03. 2006. (12:21:57)
Postovi: (28)16
|
 Postano: 20:52 uto, 1. 8. 2006 Naslov: Postano: 20:52 uto, 1. 8. 2006 Naslov: |
    |
|
|
E, ali za "broj je paran ako je djeljiv s 2" ne treba akko, ali za ovo treba jer ne znači li da ako je A&B istinita da su i A i B istinite?
Ali AND na hrvatskom znači i, pa je to opet i. :) MAtematika ne robuje jednom od jezika, nego općenito jeziku. To jest, nije baš da robuje, nego jezik čini matematiku, jer kad kažem "broj je paran" to je jezik, svjedno koji. Nije li tako?
Što se tiče ping-ponga, mislim da bi se moglo tako reći, ali onda mi opet nije jasna uloga jezika u matematici. :?
E, ali za "broj je paran ako je djeljiv s 2" ne treba akko, ali za ovo treba jer ne znači li da ako je A&B istinita da su i A i B istinite?
Ali AND na hrvatskom znači i, pa je to opet i.  MAtematika ne robuje jednom od jezika, nego općenito jeziku. To jest, nije baš da robuje, nego jezik čini matematiku, jer kad kažem "broj je paran" to je jezik, svjedno koji. Nije li tako? MAtematika ne robuje jednom od jezika, nego općenito jeziku. To jest, nije baš da robuje, nego jezik čini matematiku, jer kad kažem "broj je paran" to je jezik, svjedno koji. Nije li tako?
Što se tiče ping-ponga, mislim da bi se moglo tako reći, ali onda mi opet nije jasna uloga jezika u matematici. 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 22:32 uto, 1. 8. 2006 Naslov: Postano: 22:32 uto, 1. 8. 2006 Naslov: |
    |
|
|
[quote="Silver Surfer"]E, ali za "broj je paran ako je djeljiv s 2" ne treba akko, ali za ovo treba jer ne znači li da ako je A&B istinita da su i A i B istinite?[/quote]
U definicijama se podrazumijeva "ako i samo ako", ali se rijetko pise eksplicitno. Obicno se pise samo jedan smjer implikacije, no u definiciji uvijek imas ekvivalenciju.
| Silver Surfer (napisa): | | E, ali za "broj je paran ako je djeljiv s 2" ne treba akko, ali za ovo treba jer ne znači li da ako je A&B istinita da su i A i B istinite? |
U definicijama se podrazumijeva "ako i samo ako", ali se rijetko pise eksplicitno. Obicno se pise samo jedan smjer implikacije, no u definiciji uvijek imas ekvivalenciju.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
|












