| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:09 čet, 28. 9. 2006 Naslov: Postano: 23:09 čet, 28. 9. 2006 Naslov: |
    |
|
|
[quote]Možete li, molim Vas, precizirati. Jeste li konstrukcijom ''kao takvi" željeli izraziti bit pojma broj, ili pojmiti sam pojam broja? [/quote]
brojevi, brojevi, brojevi... prirodni, realni, nule, beskonačnosti.. pa to smo izmislili (simbole) samo da nam bude lakše zapisivati, da ne koristimo crte, točke, i što ja znam već... što znači pojmiti broj? u kom smislu? kao količinu nečeg? kao veličinu nečeg? kao redni broj nečeg? odnos imeđu dva broja, kao sam za sebe... ova rasprava je besmislena koliko i računanje sa beskonačno... broj nikad nije sam sebi svrha
bit broja?! bit broja je relativna. ovisi za što ga služim.
evo kao umjetnik, napravih [url=http://web.studenti.math.hr/~fsrica//graphic/svemir.swf]ovo[/url]
| Citat: | | Možete li, molim Vas, precizirati. Jeste li konstrukcijom ''kao takvi" željeli izraziti bit pojma broj, ili pojmiti sam pojam broja? |
brojevi, brojevi, brojevi... prirodni, realni, nule, beskonačnosti.. pa to smo izmislili (simbole) samo da nam bude lakše zapisivati, da ne koristimo crte, točke, i što ja znam već... što znači pojmiti broj? u kom smislu? kao količinu nečeg? kao veličinu nečeg? kao redni broj nečeg? odnos imeđu dva broja, kao sam za sebe... ova rasprava je besmislena koliko i računanje sa beskonačno... broj nikad nije sam sebi svrha
bit broja?! bit broja je relativna. ovisi za što ga služim.
evo kao umjetnik, napravih ovo
Zadnja promjena: Saf; 19:17 pet, 20. 10. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
 Postano: 9:57 sub, 30. 9. 2006 Naslov: Postano: 9:57 sub, 30. 9. 2006 Naslov: |
    |
|
|
[quote="Grga"]Buduci da sam se vec jednom "hrvao" s osobom koja je isti ovaj "problem" iznijela, osjecam veliku potrebu da odgovorim na ovaj topic 8)
Problem je u tome sto ti pretpostavljas
[latex]0.\underbrace{0\dots 0}_\infty1 > 0[/latex]
Ali onda po Arhimedovom aksiomu (koji je intuitivno sasvim jasan) postoji neki prirodan broj n takav da je
[latex]n \cdot 0.\underbrace{0\dots 0}_\infty1 > 1 \Longrightarrow n > 10^\infty[/latex]
sto ocito nije moguce, jer je n prirodan broj, pa je to jednako nuli.
(ovdje se pravimo da je beskonacno broj s kojim mozes baratati, ali u principu stvar i je u tome da nije, te ne mozes reci da nakon beskonacno nula ide jedinica jer to nema smisla, buduci da cinjenica da je znamenka k na n-tom mjestu u decimalnom zapisu po definiciji znaci:
[latex]a_0.a_1 \dots a_{n-1} k = a_0.a_1 \dots a_{n-1} + \frac{k}{10^n}[/latex]
no ako je n "beskonacno", onda to jednostavno nema smisla)[/quote]
@Grga:
Zahvaljujem se. Ukazali ste mi na intuitivnu grešku. Kada bi nastavio s pitanjima, ova bi tema izgubila kontruktivnost koju sam želio ostvariti.
@ostali:
U biti, želio sam da se zapitamo, možemo li logički definirati pojam broja, na što ste me uvjerili da broj možemo definirati samo matematičkim aksiomima.
Primjetio sam da u principu postavljam pitanja koja su već za antičke grčke počeli postavljati, a danas još nisu odgovorena. Morati ću se zadovoljiti s ponuđenim aksiomima (αξιωμα).
Želio bih se još jednom zahvaliti onima koji su konstruktivno raspravljali na ovu temu.
| Grga (napisa): | Buduci da sam se vec jednom "hrvao" s osobom koja je isti ovaj "problem" iznijela, osjecam veliku potrebu da odgovorim na ovaj topic 
Problem je u tome sto ti pretpostavljas
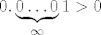
Ali onda po Arhimedovom aksiomu (koji je intuitivno sasvim jasan) postoji neki prirodan broj n takav da je
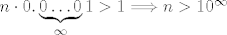
sto ocito nije moguce, jer je n prirodan broj, pa je to jednako nuli.
(ovdje se pravimo da je beskonacno broj s kojim mozes baratati, ali u principu stvar i je u tome da nije, te ne mozes reci da nakon beskonacno nula ide jedinica jer to nema smisla, buduci da cinjenica da je znamenka k na n-tom mjestu u decimalnom zapisu po definiciji znaci:
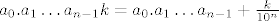
no ako je n "beskonacno", onda to jednostavno nema smisla) |
@Grga:
Zahvaljujem se. Ukazali ste mi na intuitivnu grešku. Kada bi nastavio s pitanjima, ova bi tema izgubila kontruktivnost koju sam želio ostvariti.
@ostali:
U biti, želio sam da se zapitamo, možemo li logički definirati pojam broja, na što ste me uvjerili da broj možemo definirati samo matematičkim aksiomima.
Primjetio sam da u principu postavljam pitanja koja su već za antičke grčke počeli postavljati, a danas još nisu odgovorena. Morati ću se zadovoljiti s ponuđenim aksiomima (αξιωμα).
Želio bih se još jednom zahvaliti onima koji su konstruktivno raspravljali na ovu temu.
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 11:05 sub, 30. 9. 2006 Naslov: Postano: 11:05 sub, 30. 9. 2006 Naslov: |
    |
|
|
[quote="misl4vb"]Primjetio sam da u principu postavljam pitanja koja su već za antičke grčke počeli postavljati, a danas još nisu odgovorena.
[/quote]
Kolega, pitanja koja postavljas spadaju pod neodgovoriva. Naime, krecu od jedne pretpostavke (koja je, usput budi receno nefalsifikabilna u poperijanskom smislu), a to je da sve ima neku "bit", "esenciju" ("ono po cemu jest ono sto jest").
Uzaludan je pokusaj pobijanja tvrdnje "sve ima bit", ali milsim da ti mogu naglasiti da je "bit" broja znanstveno nerelevantna (tj. ne vodi novim rezultatima). Naime, osim eksplicitnih pitanja o biti broja, "bit" broja se ne pojavljuje ni na kojoj razini pitanja o brojevima (naravno, moram naglasiti da je ono sto zovem "biti" broja je zapravo "bit" praznog skupa, jer je vec pokazano da je egzistencija broja lijepo opisana egzistencijom praznog skupa).
Mozda je cak bolje da predjem na "bit" praznog skupa (pokazano da je to "logicki" ista stvar kao i "bit" broja). Prazan skup u potpunosti odgovara pojmu atomarne "ideje", "misli" (atomarne u smislu atomos, nedjeljiv) koja nema ("informacijskog", "misaonog") sadrzaja. Tako ga se i "logicki" tretira.
Vjerujem da se mozes sloziti da sam problem "biti" broja, preko "biti" praznog skupa reducirao na problem "biti" "misli". Kako je to jedno pitanje tumacejnja svijeta, dakle, svodi se na idealisticko/materijalisticku dvojbu o "biti" misli. Oba ta pogleda spadaju u nefalsifikabilne, pa nisu ni znanstveno relevantne.
'ave fun!
Sinisa
| misl4vb (napisa): | Primjetio sam da u principu postavljam pitanja koja su već za antičke grčke počeli postavljati, a danas još nisu odgovorena.
|
Kolega, pitanja koja postavljas spadaju pod neodgovoriva. Naime, krecu od jedne pretpostavke (koja je, usput budi receno nefalsifikabilna u poperijanskom smislu), a to je da sve ima neku "bit", "esenciju" ("ono po cemu jest ono sto jest").
Uzaludan je pokusaj pobijanja tvrdnje "sve ima bit", ali milsim da ti mogu naglasiti da je "bit" broja znanstveno nerelevantna (tj. ne vodi novim rezultatima). Naime, osim eksplicitnih pitanja o biti broja, "bit" broja se ne pojavljuje ni na kojoj razini pitanja o brojevima (naravno, moram naglasiti da je ono sto zovem "biti" broja je zapravo "bit" praznog skupa, jer je vec pokazano da je egzistencija broja lijepo opisana egzistencijom praznog skupa).
Mozda je cak bolje da predjem na "bit" praznog skupa (pokazano da je to "logicki" ista stvar kao i "bit" broja). Prazan skup u potpunosti odgovara pojmu atomarne "ideje", "misli" (atomarne u smislu atomos, nedjeljiv) koja nema ("informacijskog", "misaonog") sadrzaja. Tako ga se i "logicki" tretira.
Vjerujem da se mozes sloziti da sam problem "biti" broja, preko "biti" praznog skupa reducirao na problem "biti" "misli". Kako je to jedno pitanje tumacejnja svijeta, dakle, svodi se na idealisticko/materijalisticku dvojbu o "biti" misli. Oba ta pogleda spadaju u nefalsifikabilne, pa nisu ni znanstveno relevantne.
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 11:14 sub, 30. 9. 2006 Naslov: Postano: 11:14 sub, 30. 9. 2006 Naslov: |
    |
|
|
Ma gle, broj definiras pomocu skupa, a skup se ne definira jer moras od neceg pocet, nemozes beskonacno ici sve vise. U matematici se pocne sa skupom.
Dobro, dok sam piso, nisam vidio da je i cinik odgovorio, njegov odgovor je pametniji :oops:
Ma gle, broj definiras pomocu skupa, a skup se ne definira jer moras od neceg pocet, nemozes beskonacno ici sve vise. U matematici se pocne sa skupom.
Dobro, dok sam piso, nisam vidio da je i cinik odgovorio, njegov odgovor je pametniji 
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goc9999
Forumaš(ica)


Pridružen/a: 15. 10. 2003. (19:31:20)
Postovi: (238)16
Spol: 
Lokacija: Utrina
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
 Postano: 20:28 sub, 7. 10. 2006 Naslov: Postano: 20:28 sub, 7. 10. 2006 Naslov: |
    |
|
|
Transcendentnost matematike najocitija je (koliko se meni cini), u pojmovima beskonacnost, prazan skup, imaginaran broj, kao i njihove upotrebe u stvarnosti, posebice u fizici, astronomiji i sl.
Pojmove poput tocka beskonacne zakrivljenosti prostorvremena (singularnost npr. crne rupe), prostor kao nositelj materije, imaginarno vrijeme i sl. cini se da cu tek zavrsetkom studija matematike moci poceti matematicki pojmiti.
Nadam se da necu postati usamljeni entuzijast kojega ce okolina demotivirati u nastojanju da pojmi svijet koji ga okruzuje.
Transcendentnost matematike najocitija je (koliko se meni cini), u pojmovima beskonacnost, prazan skup, imaginaran broj, kao i njihove upotrebe u stvarnosti, posebice u fizici, astronomiji i sl.
Pojmove poput tocka beskonacne zakrivljenosti prostorvremena (singularnost npr. crne rupe), prostor kao nositelj materije, imaginarno vrijeme i sl. cini se da cu tek zavrsetkom studija matematike moci poceti matematicki pojmiti.
Nadam se da necu postati usamljeni entuzijast kojega ce okolina demotivirati u nastojanju da pojmi svijet koji ga okruzuje.
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 21:45 sub, 7. 10. 2006 Naslov: Postano: 21:45 sub, 7. 10. 2006 Naslov: |
    |
|
|
[quote="misl4vb"]Transcendentnost matematike najocitija je (koliko se meni cini), u pojmovima beskonacnost, prazan skup, imaginaran broj, kao i njihove upotrebe u stvarnosti, posebice u fizici, astronomiji i sl.[/quote]
Matematika po tebi nadilazi (trans+cedere) sto tocno? I kako se tocno "nadilazenje" (necega) vidi u primjeni toga istoga u stvarnosti.
Pretpostavljam (na trenutak) da si htio reci da matematika transcesira stvarnost, a argument za to ti je koristenje matematickih pojmova u fizici (i.e. prirodi) -- dakle u stvarnosti. Drugim rijecima, ocito je da je nesto transcedentno jer ima konkretne primjene?
Okej, dakle, ne argumentiras transcesiranje stvarnosti (tertium non datur). Problem je sto onda tvoja recenica zvuci jako pametno, ali nema puno znacenja (jer bez navodjenja sto se transcesira, pretpostavlja se transcesija stvarnosti).
[quote="misl4vb"]Pojmove poput tocka beskonacne zakrivljenosti prostorvremena (singularnost npr. crne rupe), prostor kao nositelj materije, imaginarno vrijeme i sl. cini se da cu tek zavrsetkom studija matematike moci poceti matematicki pojmiti.[/quote]
Ne, do kraja studija matematike neces naletiti ni na koji od tih kozmoloskih pojmova. Barem ne kod nas. Njihovo "poimanje", na nacin na koji ti zelis "pojmiti" broj ili bilo sta drugo je prilicno apsurdno (kao sto je krcko rekao, ne mozes se rukovati sa brojem 2 (o dorucku necu)).
Najkorisniju recenicu o matematici u fizici rekao je mr. Vakula na prezentaciji svog rada u Drzavnom hidrometeoroloskom zavodu: "Mi trazimo formule koje se ponasaju kao jezero ili kao oblak."
Ponasaju kao. Ne "jesu" -- "ponasaju se kao". Pitanje egzistencije i svojstava crnih rupa i ostalih kozmoloskih objekata je jedno. Pitanje diferencijalne geometrije tocke u sustavu jednadzbi teorije opce relativnosti je nesto drugo. Ako ti se kava prolije preko crne rupe, nema vise kave. Ako ti se kava prolije po papiru gdje pises diferencijalne jednadzbe koje opisuju crnu rupu -- nema vise diferencijalnih jednadzbi. No, numericki rezultat te diferencijalne jednadzbe ocekujes da ce se poklopiti sa rezultatima mjerenja.
Pojmovi tipa imaginarno vrijeme napadaju stvar iz drugog smjera. Uzmes neki matematicki pojam (jednadzbu, rjesenje, stagod) i pitas se, odgovara li taj pojam icemu. Taj pristup cesto ide uz "shut up and calculate" princip -- imas formulu, gledaj rezultat, ne "fizicki smisao" svakog koraka.
[quote="misl4vb"]Nadam se da necu postati usamljeni entuzijast kojega ce okolina demotivirati u nastojanju da pojmi svijet koji ga okruzuje.[/quote]
Bojim se da ti moram umanjiti entuzijazam i barem djelomicno te demotivirati -- vec je zakljuceno da stanu tocno 42 andjela na vrh igle. Ni vise ni manje.
'ave fun!
Sinisa
| misl4vb (napisa): | | Transcendentnost matematike najocitija je (koliko se meni cini), u pojmovima beskonacnost, prazan skup, imaginaran broj, kao i njihove upotrebe u stvarnosti, posebice u fizici, astronomiji i sl. |
Matematika po tebi nadilazi (trans+cedere) sto tocno? I kako se tocno "nadilazenje" (necega) vidi u primjeni toga istoga u stvarnosti.
Pretpostavljam (na trenutak) da si htio reci da matematika transcesira stvarnost, a argument za to ti je koristenje matematickih pojmova u fizici (i.e. prirodi) – dakle u stvarnosti. Drugim rijecima, ocito je da je nesto transcedentno jer ima konkretne primjene?
Okej, dakle, ne argumentiras transcesiranje stvarnosti (tertium non datur). Problem je sto onda tvoja recenica zvuci jako pametno, ali nema puno znacenja (jer bez navodjenja sto se transcesira, pretpostavlja se transcesija stvarnosti).
| misl4vb (napisa): | | Pojmove poput tocka beskonacne zakrivljenosti prostorvremena (singularnost npr. crne rupe), prostor kao nositelj materije, imaginarno vrijeme i sl. cini se da cu tek zavrsetkom studija matematike moci poceti matematicki pojmiti. |
Ne, do kraja studija matematike neces naletiti ni na koji od tih kozmoloskih pojmova. Barem ne kod nas. Njihovo "poimanje", na nacin na koji ti zelis "pojmiti" broj ili bilo sta drugo je prilicno apsurdno (kao sto je krcko rekao, ne mozes se rukovati sa brojem 2 (o dorucku necu)).
Najkorisniju recenicu o matematici u fizici rekao je mr. Vakula na prezentaciji svog rada u Drzavnom hidrometeoroloskom zavodu: "Mi trazimo formule koje se ponasaju kao jezero ili kao oblak."
Ponasaju kao. Ne "jesu" – "ponasaju se kao". Pitanje egzistencije i svojstava crnih rupa i ostalih kozmoloskih objekata je jedno. Pitanje diferencijalne geometrije tocke u sustavu jednadzbi teorije opce relativnosti je nesto drugo. Ako ti se kava prolije preko crne rupe, nema vise kave. Ako ti se kava prolije po papiru gdje pises diferencijalne jednadzbe koje opisuju crnu rupu – nema vise diferencijalnih jednadzbi. No, numericki rezultat te diferencijalne jednadzbe ocekujes da ce se poklopiti sa rezultatima mjerenja.
Pojmovi tipa imaginarno vrijeme napadaju stvar iz drugog smjera. Uzmes neki matematicki pojam (jednadzbu, rjesenje, stagod) i pitas se, odgovara li taj pojam icemu. Taj pristup cesto ide uz "shut up and calculate" princip – imas formulu, gledaj rezultat, ne "fizicki smisao" svakog koraka.
| misl4vb (napisa): | | Nadam se da necu postati usamljeni entuzijast kojega ce okolina demotivirati u nastojanju da pojmi svijet koji ga okruzuje. |
Bojim se da ti moram umanjiti entuzijazam i barem djelomicno te demotivirati – vec je zakljuceno da stanu tocno 42 andjela na vrh igle. Ni vise ni manje.
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
 Postano: 8:24 ned, 8. 10. 2006 Naslov: Postano: 8:24 ned, 8. 10. 2006 Naslov: |
    |
|
[quote="cinik"]Pretpostavljam (na trenutak) da si htio reci da matematika transcesira stvarnost, a argument za to ti je koristenje matematickih pojmova u fizici (i.e. prirodi) -- dakle u stvarnosti. Drugim rijecima, ocito je da je nesto transcedentno jer ima konkretne primjene?[/quote]
Ispricavam se.
Pretpostavio sam da ce se razumjeti da govorim u kontekstu uma. Kontekst je razmišljanje i domišljanje.
Ispričavam se ponovo.
[quote="cinik"]Problem je sto onda tvoja recenica zvuci jako pametno[/quote]
:lol: (Kako kome)
[quote="cinik"]vec je zakljuceno da stanu tocno 42 andjela na vrh igle. Ni vise ni manje.[/quote]
:?:

[color=blue]Jedan imaginarni quote je nestao, a Vi, kolega, proucite Pravila ponašanja da se tao nesto ne bi ponovilo.[/color] | cinik (napisa): | | Pretpostavljam (na trenutak) da si htio reci da matematika transcesira stvarnost, a argument za to ti je koristenje matematickih pojmova u fizici (i.e. prirodi) – dakle u stvarnosti. Drugim rijecima, ocito je da je nesto transcedentno jer ima konkretne primjene? |
Ispricavam se.
Pretpostavio sam da ce se razumjeti da govorim u kontekstu uma. Kontekst je razmišljanje i domišljanje.
Ispričavam se ponovo.
| cinik (napisa): | | Problem je sto onda tvoja recenica zvuci jako pametno |
 (Kako kome) (Kako kome)
| cinik (napisa): | | vec je zakljuceno da stanu tocno 42 andjela na vrh igle. Ni vise ni manje. |


Jedan imaginarni quote je nestao, a Vi, kolega, proucite Pravila ponašanja da se tao nesto ne bi ponovilo.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Michiko
Forumaš(ica)


Pridružen/a: 10. 11. 2007. (17:46:50)
Postovi: (A)16
Spol: 
|
 Postano: 8:34 ned, 11. 11. 2007 Naslov: Postano: 8:34 ned, 11. 11. 2007 Naslov: |
    |
|
|
Eh, cinice,
mladu njeznu dusu tako satrti sa nepotrebno velikim rijecima.
Imas li ti uopce romantike u sebi? :D
Vec je od pocetka bilo jasno da se ne radi o znanstvenoj upotrebljivosti te teme vec o pokusaju filozofskog promisljanja.
I citiram: "Sto je istina?", Poncije Pilat :D
A, Misl4vbe, proucavajuci matematiku naucit ces bolje koristiti matematicke pojmove i bolje logicki rasudjivati pa ces moci ta pitanja koja naslucujes smislenije postaviti. Podrzavam tvoj entuzijazam! ;)
(I da, cinice, pitam se da li je imalo svrhe to ti napisati ali, ako sam ja Don Quijote, ti si vjetrenjaca! :D)
Eh, cinice,
mladu njeznu dusu tako satrti sa nepotrebno velikim rijecima.
Imas li ti uopce romantike u sebi? :D
Vec je od pocetka bilo jasno da se ne radi o znanstvenoj upotrebljivosti te teme vec o pokusaju filozofskog promisljanja.
I citiram: "Sto je istina?", Poncije Pilat :D
A, Misl4vbe, proucavajuci matematiku naucit ces bolje koristiti matematicke pojmove i bolje logicki rasudjivati pa ces moci ta pitanja koja naslucujes smislenije postaviti. Podrzavam tvoj entuzijazam! ;)
(I da, cinice, pitam se da li je imalo svrhe to ti napisati ali, ako sam ja Don Quijote, ti si vjetrenjaca! :D)
|
|
| [Vrh] |
|
Michiko
Forumaš(ica)


Pridružen/a: 10. 11. 2007. (17:46:50)
Postovi: (A)16
Spol: 
|
 Postano: 6:58 sri, 14. 11. 2007 Naslov: Pogovor Postano: 6:58 sri, 14. 11. 2007 Naslov: Pogovor |
    |
|
|
"Cinizam je jedina forma u kojoj priproste duse okrznu ono sto je cestitost;
a visemu covjeku valja otvoriti usi pri svakom grubljemu i finijemu cinizmu
te svaki put pozeljeti srecu, kada se pred njegovim ocima oglase besramni
komedijas ili znanstveni satir."
F. Nietzsche, [i]S onu stranu dobra i zla[/i]
EDIT:
Znam da sam naporna ali bas sam se uzrujala :-)
[b]transcendentalan[/b]
koji je prije svakog iskustva, odnosi se na uvjete spoznavanja predmeta koji su po postanku prije iskustva; prediskustven
[b]transcendentalnost[/b]
stanje onoga sto je transcendentalno
[b]transcendirati[/b]
prijeci, prelaziti granice iskustva, biti izvan ili iznad osjetilnog opazanja
(gl. im. [b]transcendiranje[/b])
Preporucila bih, ako se vec mislite skrivati iza pet(ili vise)sloznih rijeci, da zavirite prije u rjecnik. Ako ne zbog znacenja (koje vam ocito nije bitno) onda bar da u zamahu tastine ne izmisljate nove.
"Cinizam je jedina forma u kojoj priproste duse okrznu ono sto je cestitost;
a visemu covjeku valja otvoriti usi pri svakom grubljemu i finijemu cinizmu
te svaki put pozeljeti srecu, kada se pred njegovim ocima oglase besramni
komedijas ili znanstveni satir."
F. Nietzsche, S onu stranu dobra i zla
EDIT:
Znam da sam naporna ali bas sam se uzrujala :-)
transcendentalan
koji je prije svakog iskustva, odnosi se na uvjete spoznavanja predmeta koji su po postanku prije iskustva; prediskustven
transcendentalnost
stanje onoga sto je transcendentalno
transcendirati
prijeci, prelaziti granice iskustva, biti izvan ili iznad osjetilnog opazanja
(gl. im. transcendiranje)
Preporucila bih, ako se vec mislite skrivati iza pet(ili vise)sloznih rijeci, da zavirite prije u rjecnik. Ako ne zbog znacenja (koje vam ocito nije bitno) onda bar da u zamahu tastine ne izmisljate nove.
|
|
| [Vrh] |
|
|















