| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Maroje
Forumaš(ica)

Pridružen/a: 20. 03. 2003. (08:49:56)
Postovi: (8F)16
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 14:21 ned, 22. 10. 2006 Naslov: Postano: 14:21 ned, 22. 10. 2006 Naslov: |
    |
|
|
Ja mislim da ih ima [latex]\left( \begin{array}{l}
56 \\
29 \\
\end{array} \right)[/latex]
Evo, u ovaj post ću nagurat i pitanje.
Neka je zadan multiskup M=({a,b,c,d},m), m(a)=12, m(b)=10, m(c)=5 i m(d)=3. Koliko postoji podmultiskupova multiskupa M od 15 elemenata?
Ne zanima me riješenje, nego samo kako se općenito postaviti u takvoj situaciji.
Zapravo, nagađam da je riješenje [latex]\left( {\left( \begin{array}{c}
30 \\
15 \\
\end{array} \right)} \right)[/latex] možda čak i sam skužim zašto
Ja mislim da ih ima 
Evo, u ovaj post ću nagurat i pitanje.
Neka je zadan multiskup M=({a,b,c,d},m), m(a)=12, m(b)=10, m(c)=5 i m(d)=3. Koliko postoji podmultiskupova multiskupa M od 15 elemenata?
Ne zanima me riješenje, nego samo kako se općenito postaviti u takvoj situaciji.
Zapravo, nagađam da je riješenje 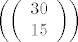 možda čak i sam skužim zašto možda čak i sam skužim zašto
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Maroje
Forumaš(ica)

Pridružen/a: 20. 03. 2003. (08:49:56)
Postovi: (8F)16
|
|
| [Vrh] |
|
Maroje
Forumaš(ica)

Pridružen/a: 20. 03. 2003. (08:49:56)
Postovi: (8F)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 23:47 pon, 23. 10. 2006 Naslov: Postano: 23:47 pon, 23. 10. 2006 Naslov: |
    |
|
|
Sad sam htio objavit brojčana rješenja iz kojih se ne vidi postupak, al onda sam se sjetio da bi bilo kompliciranije asistentima za provjeriti da li je postupak točan, ovak sam pogledaju rezultat.
@maroje, ako možete odgovoriti da li bi to bilo u redu, bio bih vam zahvalan, ako ne bi, neću stavit. Osim ovog što sam gore napiso, ne vidim razlog zašt si ljudi ne bi usporedili rješenja.
Pohvala zadaćama što su tak teške, na analizi je bilo super što su zadaće bile puno teže od kolokvija (jedino što mi treba otprilike 1 dan da je riješim). Nadam se da će i ovdje kolokviji bit lakši od zadaća.
Sad sam htio objavit brojčana rješenja iz kojih se ne vidi postupak, al onda sam se sjetio da bi bilo kompliciranije asistentima za provjeriti da li je postupak točan, ovak sam pogledaju rezultat.
@maroje, ako možete odgovoriti da li bi to bilo u redu, bio bih vam zahvalan, ako ne bi, neću stavit. Osim ovog što sam gore napiso, ne vidim razlog zašt si ljudi ne bi usporedili rješenja.
Pohvala zadaćama što su tak teške, na analizi je bilo super što su zadaće bile puno teže od kolokvija (jedino što mi treba otprilike 1 dan da je riješim). Nadam se da će i ovdje kolokviji bit lakši od zadaća.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Maroje
Forumaš(ica)

Pridružen/a: 20. 03. 2003. (08:49:56)
Postovi: (8F)16
|
 Postano: 18:48 uto, 24. 10. 2006 Naslov: Postano: 18:48 uto, 24. 10. 2006 Naslov: |
    |
|
|
[quote="alen"]Sad sam htio objavit brojčana rješenja iz kojih se ne vidi postupak, al onda sam se sjetio da bi bilo kompliciranije asistentima za provjeriti da li je postupak točan, ovak sam pogledaju rezultat.
@maroje, ako možete odgovoriti da li bi to bilo u redu, bio bih vam zahvalan, ako ne bi, neću stavit. Osim ovog što sam gore napiso, ne vidim razlog zašt si ljudi ne bi usporedili rješenja.[/quote]
Ok.
[quote="alen"]
Pohvala zadaćama što su tak teške, na analizi je bilo super što su zadaće bile puno teže od kolokvija (jedino što mi treba otprilike 1 dan da je riješim). Nadam se da će i ovdje kolokviji bit lakši od zadaća.[/quote]
U nadi je spas. :D Trebale bi biti lakši...
| alen (napisa): | Sad sam htio objavit brojčana rješenja iz kojih se ne vidi postupak, al onda sam se sjetio da bi bilo kompliciranije asistentima za provjeriti da li je postupak točan, ovak sam pogledaju rezultat.
@maroje, ako možete odgovoriti da li bi to bilo u redu, bio bih vam zahvalan, ako ne bi, neću stavit. Osim ovog što sam gore napiso, ne vidim razlog zašt si ljudi ne bi usporedili rješenja. |
Ok.
| alen (napisa): |
Pohvala zadaćama što su tak teške, na analizi je bilo super što su zadaće bile puno teže od kolokvija (jedino što mi treba otprilike 1 dan da je riješim). Nadam se da će i ovdje kolokviji bit lakši od zadaća. |
U nadi je spas.  Trebale bi biti lakši... Trebale bi biti lakši...
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 19:09 uto, 24. 10. 2006 Naslov: Postano: 19:09 uto, 24. 10. 2006 Naslov: |
    |
|
|
Wheeee, hvala.
1. a) 21
b) 125
2. Evo rješenja za n=38, to će morat bit dovoljno dobro
a) 523022617466601111760007224100074291200000000
b) 8200794532637891559375
d) 3446310324346630677300
Hmm... ajd i za n=12
a) 479001600
b) 10395
d) 1352078
3. a) 9
4. 4004
5. 4000
6. jesmo-vraćamo 64, jesmo-ne vraćamo 24, nismo-ne vraćamo 4, nismo-vraćamo 20
7. 6
8. a) 531441
b) 13841287201
c) 34650
Još jednom hvala Maroju
Wheeee, hvala.
1. a) 21
b) 125
2. Evo rješenja za n=38, to će morat bit dovoljno dobro
a) 523022617466601111760007224100074291200000000
b) 8200794532637891559375
d) 3446310324346630677300
Hmm... ajd i za n=12
a) 479001600
b) 10395
d) 1352078
3. a) 9
4. 4004
5. 4000
6. jesmo-vraćamo 64, jesmo-ne vraćamo 24, nismo-ne vraćamo 4, nismo-vraćamo 20
7. 6
8. a) 531441
b) 13841287201
c) 34650
Još jednom hvala Maroju
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 11:38 sri, 25. 10. 2006 Naslov: Postano: 11:38 sri, 25. 10. 2006 Naslov: |
    |
|
|
[quote="nana"]Stvarno ne razumijem tu tvoju neopisivu zelju da stavis rjesenja. Zar ti nije dovoljno provjerit s jos par ljudi?
Ne znam bi li se sad trebala divit ili sto? :roll: Ako postoji neki problematicni zadatak mislim da nitko ne bi imao nista protiv da ga se komentira.
Em glumis demosa iz analize :roll: , em tu izmisljas da sam rekla 2 i jos krades moja rjesenja, strah me pomislit sto je sljedece....
:twisted:[/quote]
Joj, skužila si me, to su sve moja nastojanja da te zadivim svojim velikim... poznavanjem diskretne matematike.
Nemoj se izvačit, rekla si 2, duguješ mi 1 lipu. Hm, ako se zajedničko rješavanje zove krađa... (oboje znamo koliki su omjeri čijih doprinosa tim rješenjima :twisted: )
| nana (napisa): | Stvarno ne razumijem tu tvoju neopisivu zelju da stavis rjesenja. Zar ti nije dovoljno provjerit s jos par ljudi?
Ne znam bi li se sad trebala divit ili sto?  Ako postoji neki problematicni zadatak mislim da nitko ne bi imao nista protiv da ga se komentira. Ako postoji neki problematicni zadatak mislim da nitko ne bi imao nista protiv da ga se komentira.
Em glumis demosa iz analize  , em tu izmisljas da sam rekla 2 i jos krades moja rjesenja, strah me pomislit sto je sljedece.... , em tu izmisljas da sam rekla 2 i jos krades moja rjesenja, strah me pomislit sto je sljedece....
 |
Joj, skužila si me, to su sve moja nastojanja da te zadivim svojim velikim... poznavanjem diskretne matematike.
Nemoj se izvačit, rekla si 2, duguješ mi 1 lipu. Hm, ako se zajedničko rješavanje zove krađa... (oboje znamo koliki su omjeri čijih doprinosa tim rješenjima  ) )
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
aska
Forumaš(ica)
Pridružen/a: 02. 11. 2005. (20:01:50)
Postovi: (5B)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 17:48 pet, 27. 10. 2006 Naslov: Postano: 17:48 pet, 27. 10. 2006 Naslov: |
    |
|
|
[quote="aska"][quote="Nesi"]a koliko ti je rjesenje za npr n=17?[/quote]
0.
(alen se valjda nece ljutiti sto je propustio priliku da pokaze svoje veliko poznavanje diskretne matematike :oops: :wink: )[/quote]
Ovo smatram osobnom uvredom. Mislim da je pitanje bilo postavljeno meni, i da sam jedino ja smio odgovorit na njega... :lol: Ovak ispada da to nisam znao sam :evil: , jako sam ljut...
Nisam htio stavit jer sam mislio da bi se Maroje naljutio što zloupotrebljavam njegovu dobru volju.
Danas je imao baš dobre vježbe (moram se malo ulizivat, možda budem cijela rješenja mogao objavljivat :lol: ... Al bez šale, stvarno su bile dobre vježbe)
| aska (napisa): | | Nesi (napisa): | | a koliko ti je rjesenje za npr n=17? |
0.
(alen se valjda nece ljutiti sto je propustio priliku da pokaze svoje veliko poznavanje diskretne matematike   ) ) |
Ovo smatram osobnom uvredom. Mislim da je pitanje bilo postavljeno meni, i da sam jedino ja smio odgovorit na njega...  Ovak ispada da to nisam znao sam Ovak ispada da to nisam znao sam  , jako sam ljut... , jako sam ljut...
Nisam htio stavit jer sam mislio da bi se Maroje naljutio što zloupotrebljavam njegovu dobru volju.
Danas je imao baš dobre vježbe (moram se malo ulizivat, možda budem cijela rješenja mogao objavljivat  ... Al bez šale, stvarno su bile dobre vježbe) ... Al bez šale, stvarno su bile dobre vježbe)
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 9:58 uto, 31. 10. 2006 Naslov: Postano: 9:58 uto, 31. 10. 2006 Naslov: |
    |
|
|
Evo, pošto su svi ljudi različiti za okruglim stolom, uzmeš neko mjesto otkud ćeš gledat. E, sad ću se ja pravit da sam već izabrao 5 ljudi koje stavljam natrag za stol, ali da sam radio isto što i sada radim, ali suprotnim redom.
Znači, imam 15 ljudi za stolom i 5 praznih mjesta. Moram izabrat 5 praznih mjesta tak da nikoja 2 ne budu susjedna.
Sad se sjetim da imam početak od kojeg gledam, i popisujem sve ljude u smjeru kazaljke na satu. Uočim da 5 rupa koje imam međusobno ne razlikujem jer se točno zna tko je sjedio na kojoj rupi. Imat ću 3 slučaja:
1) 0_0_0_0_0_0_0_0_0_0_0_0_0_0_0 i raspoređujem jedinice (njih 5) na prazna mjesta, a zatim poništim preostale praznine, "spojim niz".
2) 10_0_0_0_0_0_0_0_0_0_0_0_0_0_0 i raspoređujem 4 jedinice
3) 0_0_0_0_0_0_0_0_0_0_0_0_0_0_01 i raspoređujem 4 jedinice
Slučajevi su disjunktni, bla bla...
Evo, nadam se da je bilo jasno
Da samo dodam, ovo Rješenje©®™ je vlasništvo kolegice nane.
Evo, pošto su svi ljudi različiti za okruglim stolom, uzmeš neko mjesto otkud ćeš gledat. E, sad ću se ja pravit da sam već izabrao 5 ljudi koje stavljam natrag za stol, ali da sam radio isto što i sada radim, ali suprotnim redom.
Znači, imam 15 ljudi za stolom i 5 praznih mjesta. Moram izabrat 5 praznih mjesta tak da nikoja 2 ne budu susjedna.
Sad se sjetim da imam početak od kojeg gledam, i popisujem sve ljude u smjeru kazaljke na satu. Uočim da 5 rupa koje imam međusobno ne razlikujem jer se točno zna tko je sjedio na kojoj rupi. Imat ću 3 slučaja:
1) 0_0_0_0_0_0_0_0_0_0_0_0_0_0_0 i raspoređujem jedinice (njih 5) na prazna mjesta, a zatim poništim preostale praznine, "spojim niz".
2) 10_0_0_0_0_0_0_0_0_0_0_0_0_0_0 i raspoređujem 4 jedinice
3) 0_0_0_0_0_0_0_0_0_0_0_0_0_0_01 i raspoređujem 4 jedinice
Slučajevi su disjunktni, bla bla...
Evo, nadam se da je bilo jasno
Da samo dodam, ovo Rješenje©®™ je vlasništvo kolegice nane.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 11:19 uto, 31. 10. 2006; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
|









