| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
linearna
Gost
|
|
| [Vrh] |
|
crnka
Forumaš(ica)

Pridružen/a: 30. 01. 2007. (20:03:59)
Postovi: (31)16
|
 Postano: 20:36 ned, 18. 2. 2007 Naslov: Postano: 20:36 ned, 18. 2. 2007 Naslov: |
    |
|
|
Skup S={v1,...,vn} je sistem izvodnica za vektorski prostor V. Ako je linearno nezavisan, onda je baza i dimV=n.
Ako je zavisan, može se reducirati do baze, tj. postoji vektor v koji se može prikazati kao linearna kombinacija preostalih.
Tada je i S\{v} sistem izvodnica za V. Ako je linearno nezavisan, baza je i dimV=n-1.
.
.
.
U "najgorem" slučaju ti mogu svi v1=v2=...=vn=0 i tada je dimV=0.
Dakle, dimV<=n.
A ovo dimV>=0 ne vrijedi jer dimV ne može biti veća od n.
Nadam se da je pomoglo... :P
Skup S={v1,...,vn} je sistem izvodnica za vektorski prostor V. Ako je linearno nezavisan, onda je baza i dimV=n.
Ako je zavisan, može se reducirati do baze, tj. postoji vektor v koji se može prikazati kao linearna kombinacija preostalih.
Tada je i S\{v} sistem izvodnica za V. Ako je linearno nezavisan, baza je i dimV=n-1.
.
.
.
U "najgorem" slučaju ti mogu svi v1=v2=...=vn=0 i tada je dimV=0.
Dakle, dimV<=n.
A ovo dimV>=0 ne vrijedi jer dimV ne može biti veća od n.
Nadam se da je pomoglo... 
|
|
| [Vrh] |
|
inja17
Forumaš(ica)

Pridružen/a: 18. 02. 2007. (20:08:31)
Postovi: (3)16
|
 Postano: 20:49 ned, 18. 2. 2007 Naslov: linearna Postano: 20:49 ned, 18. 2. 2007 Naslov: linearna |
    |
|
|
je puno ti hvala i imam još jedno pitanje koje mi je klimavo. presjek dva poptrosotra nekog vektorskog prosotra može biti prazan skup?
EDIT: krivo sam napisala pitanje, L je potprostor od V, tada uvijek postoji K, koji je također potprostor od V, takav da L presjek K bude prazan skup. al to ide isto na tu foru?
je puno ti hvala i imam još jedno pitanje koje mi je klimavo. presjek dva poptrosotra nekog vektorskog prosotra može biti prazan skup?
EDIT: krivo sam napisala pitanje, L je potprostor od V, tada uvijek postoji K, koji je također potprostor od V, takav da L presjek K bude prazan skup. al to ide isto na tu foru?
Zadnja promjena: inja17; 21:13 ned, 18. 2. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
 Postano: 21:02 ned, 18. 2. 2007 Naslov: Postano: 21:02 ned, 18. 2. 2007 Naslov: |
    |
|
|
pa,da!
ako uzmeno da je A{x1,...,xk} a B{x(malo k+1),...,xn};
ApresB=0
pa,da!
ako uzmeno da je A{x1,...,xk} a B{x(malo k+1),...,xn};
ApresB=0
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
crnka
Forumaš(ica)

Pridružen/a: 30. 01. 2007. (20:03:59)
Postovi: (31)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 19:21 pon, 19. 2. 2007 Naslov: Postano: 19:21 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="ivanzub"]moze mala pomoc oko ovih zadataka:
4. ako su svi dijagonalni elementi matrice A jednaki nula,onda je A singularna DA ili NE i zasto
[/quote]
Ako je A iz Mn, i ako je [latex]a_{ii} = 0[/latex], za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti [b]taj[/b] rang govori o regularnosti/singularnosti matrice A?
| ivanzub (napisa): | moze mala pomoc oko ovih zadataka:
4. ako su svi dijagonalni elementi matrice A jednaki nula,onda je A singularna DA ili NE i zasto
|
Ako je A iz Mn, i ako je 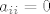 , za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti taj rang govori o regularnosti/singularnosti matrice A? , za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti taj rang govori o regularnosti/singularnosti matrice A?
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 19:29 pon, 19. 2. 2007 Naslov: Postano: 19:29 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="herman"]
Ako je A iz Mn, i ako je [latex]a_{ii} = 0[/latex], za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti [b]taj[/b] rang govori o regularnosti/singularnosti matrice A?[/quote]
Cinjenica da su na dijagonali nule o rangu matrice ne govori apsolutno nista. :wink:
| herman (napisa): |
Ako je A iz Mn, i ako je 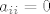 , za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti taj rang govori o regularnosti/singularnosti matrice A? , za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti taj rang govori o regularnosti/singularnosti matrice A? |
Cinjenica da su na dijagonali nule o rangu matrice ne govori apsolutno nista. 
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
nymeria
Forumaš(ica)


Pridružen/a: 27. 10. 2006. (21:00:29)
Postovi: (10)16
Spol: 
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 22:06 pon, 19. 2. 2007 Naslov: Postano: 22:06 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="mdoko"][quote="herman"]
Ako je A iz Mn, i ako je [latex]a_{ii} = 0[/latex], za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti [b]taj[/b] rang govori o regularnosti/singularnosti matrice A?[/quote]
Cinjenica da su na dijagonali nule o rangu matrice ne govori apsolutno nista. :wink:[/quote]
Ups, malo sam se zanio, isprika na odmaganju! :oops: Dapače, bolje da ne kažem što sam mislio o rangu u tom slučaju. :D
| mdoko (napisa): | | herman (napisa): |
Ako je A iz Mn, i ako je 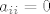 , za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti taj rang govori o regularnosti/singularnosti matrice A? , za svaki i = 1, ..., n, što ti to govori o rangu matrice A? Nadalje, što ti taj rang govori o regularnosti/singularnosti matrice A? |
Cinjenica da su na dijagonali nule o rangu matrice ne govori apsolutno nista.  |
Ups, malo sam se zanio, isprika na odmaganju!  Dapače, bolje da ne kažem što sam mislio o rangu u tom slučaju. Dapače, bolje da ne kažem što sam mislio o rangu u tom slučaju. 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:12 pon, 19. 2. 2007 Naslov: Postano: 22:12 pon, 19. 2. 2007 Naslov: |
    |
|
|
[quote="ivanzub"]:([/quote]
Mušica mu tuhstih, pa napisao sam ti da imas rjesenja... sto bi vise? :shock: "Prelistaj" zadnjih par topica o teoriji i usmenima na podforumu LA i nadji. 8) Ili upotrijebi trazilicu... :faca:
[quote="nymeria"]nije nuzno singularna, nadi protuprimjer, neku matricu 2x2 s nulicama na dijagonali i lako nades da ima inverz i to bi valjda trebalo bit dovoljno...[/quote]
Ne treba niti inverz: lakse je pokazati da su stupci (ili reci) linearno nezavisni. ;)
| ivanzub (napisa): |  |
Mušica mu tuhstih, pa napisao sam ti da imas rjesenja... sto bi vise?  "Prelistaj" zadnjih par topica o teoriji i usmenima na podforumu LA i nadji. "Prelistaj" zadnjih par topica o teoriji i usmenima na podforumu LA i nadji.  Ili upotrijebi trazilicu... Ili upotrijebi trazilicu... 
| nymeria (napisa): | | nije nuzno singularna, nadi protuprimjer, neku matricu 2x2 s nulicama na dijagonali i lako nades da ima inverz i to bi valjda trebalo bit dovoljno... |
Ne treba niti inverz: lakse je pokazati da su stupci (ili reci) linearno nezavisni. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
~sanja~
Forumaš(ica)
Pridružen/a: 18. 07. 2006. (20:06:20)
Postovi: (1A)16
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 20:15 čet, 30. 8. 2007 Naslov: Postano: 20:15 čet, 30. 8. 2007 Naslov: |
    |
|
|
a pisalo se već o tome... pogledaj malo... inače, najbolje ti je da nađeš skriptu profesora bakića na netu, sve ti je lijepo objašnjeno... nauči to s razumijevanjem, sve definicije i iskaze pogotovo, dokazi nisu toliko bitni ako ne želiš neku veću ocjenu... i nauči sve, tak ti je najsigurnije, a i nema tolko puno toga :)
a pisalo se već o tome... pogledaj malo... inače, najbolje ti je da nađeš skriptu profesora bakića na netu, sve ti je lijepo objašnjeno... nauči to s razumijevanjem, sve definicije i iskaze pogotovo, dokazi nisu toliko bitni ako ne želiš neku veću ocjenu... i nauči sve, tak ti je najsigurnije, a i nema tolko puno toga 
_________________ kalendar 
  |
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Miha Keber
Forumaš(ica)

Pridružen/a: 18. 10. 2006. (20:16:56)
Postovi: (26)16
Spol: 
|
|
| [Vrh] |
|
|













