Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Integral s pismenog
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Diferencijalni račun i integrali funkcija više varijabli
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Grga
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: muško
Sarma = la pohva - posuda
99 = 124 - 25
PostPostano: 22:12 sri, 21. 2. 2007    Naslov: Integral s pismenog Citirajte i odgovorite
Bas sam se mucio s njim jedno sat i 16 minuta na pismenom i nisam se prakticki ni maknuo od pocetka.

[latex]\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\phi}\int_0^{2 - \frac{r}{\cos\phi}}rdzdrd\phi = \int_0^2 (1 - \frac{z}{2})^2\pi dz[/latex]

Treba pokazati da vrijedi gornja jednakost i skicirati i opisati tijelo ciji je volumen dan tim integralima.
Dakle probao sam polarne koordinate, to bi svelo [latex]2 - \frac{r}{\cos\phi}[/latex] na [latex]2 - \frac{x^2 + y^2}{x}[/latex] ali ona [latex]2\phi[/latex] kao gornja granica me jednostavno unistava :P
probao sam to nekak skicirat i stalno mi je negdje bjezalo u beskonacno :?
Probao sam integrirati integral kako je zadani ispalo mi je da integral ne postoji :cry:

Pa ako se da nekome bacit oko, bilo bi lijepo. I pohvala Mei za kul rok, fora su zadaci (osim ovog integrala naravno :))
Bas sam se mucio s njim jedno sat i 16 minuta na pismenom i nisam se prakticki ni maknuo od pocetka.



Treba pokazati da vrijedi gornja jednakost i skicirati i opisati tijelo ciji je volumen dan tim integralima.
Dakle probao sam polarne koordinate, to bi svelo na ali ona kao gornja granica me jednostavno unistava Razz
probao sam to nekak skicirat i stalno mi je negdje bjezalo u beskonacno Confused
Probao sam integrirati integral kako je zadani ispalo mi je da integral ne postoji Crying or Very sad

Pa ako se da nekome bacit oko, bilo bi lijepo. I pohvala Mei za kul rok, fora su zadaci (osim ovog integrala naravno Smile)



_________________
Bri
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
mea
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
Sarma = la pohva - posuda
33 = 43 - 10
PostPostano: 11:49 čet, 22. 2. 2007    Naslov: Re: Integral s pismenog Citirajte i odgovorite
[quote="Grga"]Bas sam se mucio s njim jedno sat i 16 minuta na pismenom i nisam se prakticki ni maknuo od pocetka.

[latex]\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\phi}\int_0^{2 - \frac{r}{\cos\phi}}rdzdrd\phi = \int_0^2 (1 - \frac{z}{2})^2\pi dz[/latex]

Treba pokazati da vrijedi gornja jednakost i skicirati i opisati tijelo ciji je volumen dan tim integralima.[/quote]

Kako jednostavnije pokazati da vrijedi jednakost nego izračunati obje strane i vidjeti da se dobije isto...
A skicirati tijelo.. možeš li barem onaj integral na desnoj strani shvatiti kao volumen nečega?

[quote="Grga"]I pohvala Mei za kul rok, fora su zadaci (osim ovog integrala naravno :))[/quote]
Hvala. Al' moraš priznat da ni integral nije loš.
Grga (napisa):
Bas sam se mucio s njim jedno sat i 16 minuta na pismenom i nisam se prakticki ni maknuo od pocetka.



Treba pokazati da vrijedi gornja jednakost i skicirati i opisati tijelo ciji je volumen dan tim integralima.


Kako jednostavnije pokazati da vrijedi jednakost nego izračunati obje strane i vidjeti da se dobije isto...
A skicirati tijelo.. možeš li barem onaj integral na desnoj strani shvatiti kao volumen nečega?

Grga (napisa):
I pohvala Mei za kul rok, fora su zadaci (osim ovog integrala naravno Smile)

Hvala. Al' moraš priznat da ni integral nije loš.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Grga
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: muško
Sarma = la pohva - posuda
99 = 124 - 25
PostPostano: 16:50 čet, 22. 2. 2007    Naslov: Citirajte i odgovorite
Pa probao sam ja izracunati lijevi integral, ali onda dobijem [latex]\displaystyle \frac{\pi^3}{3} - \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{8\phi^3}{3\cos\phi}d\phi[/latex] i sad kao prvo ne znam kako bih to izintegrirao samo po sebi, ali taj bih problem mozda i rijesio, da se ne radi u tome da mi funkcija koju zelim integrirati "bjezi" u beskonacnosti, pa mi nije jasno kako bi to onda trebalo biti integrabilno.
A sto se tice desnog integrala, skica je samo povrsina ispod djela parabole. Mislim, i ocekivao sam da bi u ovom drugom integralu trebao biti neki skriveni hint, ali jednostavno ga ne vidim...

Ma dobar je intregral , samo bi mi bio drazi da sam ga uspio rijesiti :P
Pa probao sam ja izracunati lijevi integral, ali onda dobijem 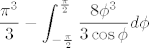i sad kao prvo ne znam kako bih to izintegrirao samo po sebi, ali taj bih problem mozda i rijesio, da se ne radi u tome da mi funkcija koju zelim integrirati "bjezi" u beskonacnosti, pa mi nije jasno kako bi to onda trebalo biti integrabilno.
A sto se tice desnog integrala, skica je samo povrsina ispod djela parabole. Mislim, i ocekivao sam da bi u ovom drugom integralu trebao biti neki skriveni hint, ali jednostavno ga ne vidim...

Ma dobar je intregral , samo bi mi bio drazi da sam ga uspio rijesiti Razz



_________________
Bri
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
mea
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
Sarma = la pohva - posuda
33 = 43 - 10
PostPostano: 17:40 čet, 22. 2. 2007    Naslov: Re: Integral s pismenog Citirajte i odgovorite
Uh. Tek sam ispravljajući pismene vidjela u čemu je problem.
Lijevi integral je trebao biti: [latex]\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\cos\phi}\int_0^{2 - \frac{r}{\cos\phi}}rdzdrd\phi[/latex]
Moje isprike svima koji su upali u probleme računajući taj integral.
Sad moram smislit kome dati koliko bodova. Zna neko neki dobar generator slučajnih brojeva?

Desni integral: po z od 0 do 2 integriramo površinu kruga (čiji se polumjer mijenja linearno ovisno o z), dakle to je volumen stošca.
Uh. Tek sam ispravljajući pismene vidjela u čemu je problem.
Lijevi integral je trebao biti:
Moje isprike svima koji su upali u probleme računajući taj integral.
Sad moram smislit kome dati koliko bodova. Zna neko neki dobar generator slučajnih brojeva?

Desni integral: po z od 0 do 2 integriramo površinu kruga (čiji se polumjer mijenja linearno ovisno o z), dakle to je volumen stošca.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 17:45 čet, 22. 2. 2007    Naslov: Re: Integral s pismenog Citirajte i odgovorite
[quote="mea"]Uh. Tek sam ispravljajući pismene vidjela u čemu je problem.
Lijevi integral je trebao biti: [latex]\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\cos\phi}\int_0^{2 - \frac{r}{\cos\phi}}rdzdrd\phi[/latex]
Moje isprike svima koji su upali u probleme računajući taj integral.
Sad moram smislit kome dati koliko bodova. Zna neko neki dobar generator slučajnih brojeva?
[/quote]
pa zar ne bi trebali svi dobiti, jer mozda su neki isli integrirati taj integral, prosli prvi, dosli do drugog i nisu znali dalje, pa nisu predali pokusaj.
mea (napisa):
Uh. Tek sam ispravljajući pismene vidjela u čemu je problem.
Lijevi integral je trebao biti:
Moje isprike svima koji su upali u probleme računajući taj integral.
Sad moram smislit kome dati koliko bodova. Zna neko neki dobar generator slučajnih brojeva?

pa zar ne bi trebali svi dobiti, jer mozda su neki isli integrirati taj integral, prosli prvi, dosli do drugog i nisu znali dalje, pa nisu predali pokusaj.



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
MB
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: muško
Sarma = la pohva - posuda
62 = 80 - 18
Lokacija: Molvice
PostPostano: 17:53 čet, 22. 2. 2007    Naslov: Citirajte i odgovorite
cuo sam zadatke i stvarno su lijepi jer nema puno racunanja. no cini mi se da bi bilo bolje da su bas takvi zadaci bili na kolokvijima, a na pismenima vise sablona. na kolokvije izlaze gotovo svi ljudi (mislim opcenito na kolegije koji normalno postoje u programu) i dobro je na takvim zadacima vidjet tko razmislja, a ako netko mora izaci vise puta na pismeni onda znaci da mu je to gradivo tesko i nije realno ocekivati da ce se sjetiti i jos nekih trikova sa strane.
cuo sam zadatke i stvarno su lijepi jer nema puno racunanja. no cini mi se da bi bilo bolje da su bas takvi zadaci bili na kolokvijima, a na pismenima vise sablona. na kolokvije izlaze gotovo svi ljudi (mislim opcenito na kolegije koji normalno postoje u programu) i dobro je na takvim zadacima vidjet tko razmislja, a ako netko mora izaci vise puta na pismeni onda znaci da mu je to gradivo tesko i nije realno ocekivati da ce se sjetiti i jos nekih trikova sa strane.



_________________
Trcim u krug od srece!
[Vrh]
Korisnički profil Pošaljite privatnu poruku Posjetite Web stranice
Grga
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: muško
Sarma = la pohva - posuda
99 = 124 - 25
PostPostano: 19:36 čet, 22. 2. 2007    Naslov: Re: Integral s pismenog Citirajte i odgovorite
[quote="mea"]Uh. Tek sam ispravljajući pismene vidjela u čemu je problem.
Lijevi integral je trebao biti: [latex]\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\cos\phi}\int_0^{2 - \frac{r}{\cos\phi}}rdzdrd\phi[/latex]
Moje isprike svima koji su upali u probleme računajući taj integral.
Sad moram smislit kome dati koliko bodova. Zna neko neki dobar generator slučajnih brojeva?

Desni integral: po z od 0 do 2 integriramo površinu kruga (čiji se polumjer mijenja linearno ovisno o z), dakle to je volumen stošca.[/quote]

Hm, ne znam. Mislim sam sam si kriv, ali ja sam predao papir na kojem sam samo napravio supstituciju i zapeo, a ona tri na koja sam pokusavao rjesavat integral i skicirat (te nisam uspio) nisam.
Mislim, postoji opcija da se zadatak ne racuna (tj da se svakome da bodova proporcionalno ostatku testa koji su rijesili), no to sad ne bi bilo fer prema ljudima koji su ipak nesto napravili, npr. skicirali stozac. Mozda da se onda njima da jos neke bodove? Mozda se meni to cini kao dobro rjesenje samo zato jer sam rijesio ostale zadatke, pa bi mi islo na ruku, ali vjerujem da bih uspio rijesiti taj zadatak da nije bilo greske, jer sam stvarno imao preko sat vremena za rijesiti ga, a inace nemam problema sa zadacima tog tipa. A i na kraju nisam stigao provjeriti prva cetiri zadatka jer sam pokusavao do kraja rijesiti peti :(
mea (napisa):
Uh. Tek sam ispravljajući pismene vidjela u čemu je problem.
Lijevi integral je trebao biti: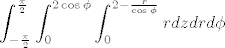
Moje isprike svima koji su upali u probleme računajući taj integral.
Sad moram smislit kome dati koliko bodova. Zna neko neki dobar generator slučajnih brojeva?

Desni integral: po z od 0 do 2 integriramo površinu kruga (čiji se polumjer mijenja linearno ovisno o z), dakle to je volumen stošca.


Hm, ne znam. Mislim sam sam si kriv, ali ja sam predao papir na kojem sam samo napravio supstituciju i zapeo, a ona tri na koja sam pokusavao rjesavat integral i skicirat (te nisam uspio) nisam.
Mislim, postoji opcija da se zadatak ne racuna (tj da se svakome da bodova proporcionalno ostatku testa koji su rijesili), no to sad ne bi bilo fer prema ljudima koji su ipak nesto napravili, npr. skicirali stozac. Mozda da se onda njima da jos neke bodove? Mozda se meni to cini kao dobro rjesenje samo zato jer sam rijesio ostale zadatke, pa bi mi islo na ruku, ali vjerujem da bih uspio rijesiti taj zadatak da nije bilo greske, jer sam stvarno imao preko sat vremena za rijesiti ga, a inace nemam problema sa zadacima tog tipa. A i na kraju nisam stigao provjeriti prva cetiri zadatka jer sam pokusavao do kraja rijesiti peti Sad



_________________
Bri
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
raspjevani_opat
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 02. 2005. (12:42:04)
Postovi: (E5)16
Sarma = la pohva - posuda
1 = 17 - 16
PostPostano: 23:08 pet, 13. 4. 2007    Naslov: Citirajte i odgovorite
moze li netko staviti na net taj zadnji rok :D

hvala
moze li netko staviti na net taj zadnji rok Very Happy

hvala


[Vrh]
Korisnički profil Pošaljite privatnu poruku
kreda
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 21. 08. 2005. (23:07:55)
Postovi: (44)16
Sarma = la pohva - posuda
3 = 7 - 4
PostPostano: 23:24 pet, 13. 4. 2007    Naslov: Citirajte i odgovorite
Pa meni se čini da su svi rokovi na netu...
Zadnji ti je 21.02.2007. na službenim stranicama kolegija...

Jel ne mreš otvorit ili kaj?

Uglavnom, attach.-at ću ti...
Pa meni se čini da su svi rokovi na netu...
Zadnji ti je 21.02.2007. na službenim stranicama kolegija...

Jel ne mreš otvorit ili kaj?

Uglavnom, attach.-at ću ti...


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 2. godine -> Diferencijalni račun i integrali funkcija više varijabli Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan