| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 19:03 čet, 29. 3. 2007 Naslov: DZ2 - pitanja Postano: 19:03 čet, 29. 3. 2007 Naslov: DZ2 - pitanja |
    |
|
|
Budem ja ponovno probio led sa pitanjima .... :D
U 1 zadatku;
Ako [latex]g\in G_x [/latex] da li onda i [latex]g^{-1} \in G_x[/latex]. No, ovako ide , ako [latex] g\in G_x [/latex] onda [latex]gx=x=(g^{-1}g)x=\{[/latex] buduci je djelovanje vjerno [latex] \} = g^{-1}(gx)=g^{-1}x[/latex], slijedi [latex]g^{-1}\in G_x[/latex] ?
(Ako je ovo tocno onda je trazena tvrdnja skoro dokazana)
Unaprijed hvala!! :P
Edit:hvala na prijedbi. Nisam imao na umu vjernost djelovanja, nego da G djeluje na X.
Budem ja ponovno probio led sa pitanjima .... 
U 1 zadatku;
Ako 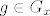 da li onda i da li onda i 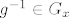 . No, ovako ide , ako . No, ovako ide , ako 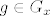 onda onda 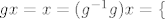 buduci je djelovanje vjerno buduci je djelovanje vjerno 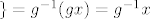 , slijedi , slijedi 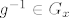 ? ?
(Ako je ovo tocno onda je trazena tvrdnja skoro dokazana)
Unaprijed hvala!! 
Edit:hvala na prijedbi. Nisam imao na umu vjernost djelovanja, nego da G djeluje na X.
Zadnja promjena: Mr.Doe; 12:11 pet, 30. 3. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 20:36 ned, 1. 4. 2007 Naslov: Postano: 20:36 ned, 1. 4. 2007 Naslov: |
    |
|
|
Za 4. zad izaberete cvrsti x_0 i elementu grupe g pridruzite element gx_0 iz skupa. To je bijekcija zbog regularnog djelovanja.
U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.
Prva bijekcija zapravo je specijalni slucaj druge.
Za 4. zad izaberete cvrsti x_0 i elementu grupe g pridruzite element gx_0 iz skupa. To je bijekcija zbog regularnog djelovanja.
U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.
Prva bijekcija zapravo je specijalni slucaj druge.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 10:10 pon, 2. 4. 2007 Naslov: Postano: 10:10 pon, 2. 4. 2007 Naslov: |
    |
|
|
Nisu mi bas jasni primitivni elementi , u knjizi tvrde da je neki element primitivan ako mozemo sve ostale elemente dobiti potenciranjem tog elementa (jos ako je usput broj elemenata,bez nule, prost ,tada su svi elementi primitivni). No u knjizi je dan primjer gdje je tocno sedam elemenata, te nam daju primjer potenciranja [latex]x[/latex] -a. No, ako uzmemo element 1 onda njegovim potenciranjem stalno dobivamo 1 ,a ne sve ostale elemente,te onda taj element ne moze biti primitivan (u knjizi se radilo o [latex]\mathbb{Z}_2[x]\backslash(x^{3}+x+1)[/latex]
Mozete li mi to pojasniti?
Nisu mi bas jasni primitivni elementi , u knjizi tvrde da je neki element primitivan ako mozemo sve ostale elemente dobiti potenciranjem tog elementa (jos ako je usput broj elemenata,bez nule, prost ,tada su svi elementi primitivni). No u knjizi je dan primjer gdje je tocno sedam elemenata, te nam daju primjer potenciranja  -a. No, ako uzmemo element 1 onda njegovim potenciranjem stalno dobivamo 1 ,a ne sve ostale elemente,te onda taj element ne moze biti primitivan (u knjizi se radilo o -a. No, ako uzmemo element 1 onda njegovim potenciranjem stalno dobivamo 1 ,a ne sve ostale elemente,te onda taj element ne moze biti primitivan (u knjizi se radilo o 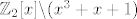
Mozete li mi to pojasniti?
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 10:14 pon, 2. 4. 2007 Naslov: Postano: 10:14 pon, 2. 4. 2007 Naslov: |
    |
|
|
[quote="krcko"]
U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.
[/quote]
Mozemo li se koristiti Lagrangeovim teoremom (kao cinjenicom)u dokazu?
(Naime,u hungerford-ovoj knjizi se dana skica dokaza :D ,gdje koristi Lagrangeov teorem)
| krcko (napisa): |
U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.
|
Mozemo li se koristiti Lagrangeovim teoremom (kao cinjenicom)u dokazu?
(Naime,u hungerford-ovoj knjizi se dana skica dokaza  ,gdje koristi Lagrangeov teorem) ,gdje koristi Lagrangeov teorem)
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 10:55 pon, 2. 4. 2007 Naslov: Postano: 10:55 pon, 2. 4. 2007 Naslov: |
    |
|
|
[quote="Mr.Doe"](jos ako je usput broj elemenata,bez nule, prost ,tada su svi elementi primitivni)... No, ako uzmemo element 1 onda njegovim potenciranjem stalno dobivamo 1 ,a ne sve ostale elemente,te onda taj element ne moze biti primitivan (u knjizi se radilo o [latex]\mathbb{Z}_2[x]\backslash(x^{3}+x+1)[/latex]
Mozete li mi to pojasniti?[/quote]
Potenciranjem jedinice dobiva se stalno jedinica, taj element nije primitivan. U knjizi je tipfeler (svi [b]ostali[/b] elementi osim 0 i 1 su primitivni ako je q-1 prost). Pri rjesavanju zadace mozete koristiti Lagrangea, Hungerforda, Bibliju i sta god vam treba. Na kolokviju ce Hungerford biti zabranjen, Lagrange dozvoljen, a za Bibliju cemo se dogovoriti :)
| Mr.Doe (napisa): | (jos ako je usput broj elemenata,bez nule, prost ,tada su svi elementi primitivni)... No, ako uzmemo element 1 onda njegovim potenciranjem stalno dobivamo 1 ,a ne sve ostale elemente,te onda taj element ne moze biti primitivan (u knjizi se radilo o 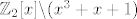
Mozete li mi to pojasniti? |
Potenciranjem jedinice dobiva se stalno jedinica, taj element nije primitivan. U knjizi je tipfeler (svi ostali elementi osim 0 i 1 su primitivni ako je q-1 prost). Pri rjesavanju zadace mozete koristiti Lagrangea, Hungerforda, Bibliju i sta god vam treba. Na kolokviju ce Hungerford biti zabranjen, Lagrange dozvoljen, a za Bibliju cemo se dogovoriti 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 16:20 pon, 2. 4. 2007 Naslov: Postano: 16:20 pon, 2. 4. 2007 Naslov: |
    |
|
|
[quote="krcko"]U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.[/quote]
Pri dokazivanju injekcije, da li prethodno fiksiramo i?
| krcko (napisa): | | U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x. |
Pri dokazivanju injekcije, da li prethodno fiksiramo i?
|
|
| [Vrh] |
|
Gost
|
 Postano: 16:40 pon, 2. 4. 2007 Naslov: Postano: 16:40 pon, 2. 4. 2007 Naslov: |
    |
|
|
[quote]U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.[/quote]
Nije mi jasno ... ako je x_i = gx, a (g_i)x=x_i onda je valjda g_i = g ???
:roll:
| Citat: | | U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x. |
Nije mi jasno ... ako je x_i = gx, a (g_i)x=x_i onda je valjda g_i = g ???

|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
 Postano: 23:38 pon, 14. 4. 2008 Naslov: Postano: 23:38 pon, 14. 4. 2008 Naslov: |
    |
|
|
[quote="krcko"]
U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.
Prva bijekcija zapravo je specijalni slucaj druge.[/quote]
Zanima me samo zasto je jedinstven g_i koji kad djuluje na x daje xi. Mora biti jer inace nije dobro definirana bijekcija.
| krcko (napisa): |
U 2. zadatku bijekcija nije onako kanonska kavu sam je zamisljao, ali se moze uspostaviti. Ako je {x_1,x_2,...,x_k} orbita od x, izaberete g_1,...,g_k iz grupe takve da je (g_i)x=x_i. Onda elementu grupe g pridruzite par (x_i,(g_i)^(-1)*g), pri cemu je x_i=gx. Dokazete da je to bijekcija izmedju grupe G i kartezijevog produkta orbite x^G sa stabilizatorom G_x.
Prva bijekcija zapravo je specijalni slucaj druge. |
Zanima me samo zasto je jedinstven g_i koji kad djuluje na x daje xi. Mora biti jer inace nije dobro definirana bijekcija.
|
|
| [Vrh] |
|
|







