| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mali_zeleni (neulogiran)
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ddz
Forumaš(ica)

Pridružen/a: 29. 10. 2004. (22:49:49)
Postovi: (4D)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
vanish
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (22:45:35)
Postovi: (6D)16
Spol: 
Lokacija: stambena zgrada
|
|
| [Vrh] |
|
Zvone
Forumaš(ica)

Pridružen/a: 01. 07. 2003. (13:09:44)
Postovi: (9D)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 13:13 ned, 15. 4. 2007 Naslov: Postano: 13:13 ned, 15. 4. 2007 Naslov: |
    |
|
|
Možda sam ja glup pa nemogu nać u bilježnici, ak ima još neko poput mene, ima dobrih primjera
[url]http://en.wikipedia.org/wiki/Linear_least_squares[/url] pod Computation, [url]http://en.wikipedia.org/wiki/Cholesky_decomposition[/url], [url]http://en.wikipedia.org/wiki/QR_decomposition#Connection_to_a_determinant_or_a_product_of_eigenvalues[/url],
[url]http://en.wikipedia.org/wiki/Singular_value_decomposition[/url]
Ko bi reko da SVD stoji za to...
Možda sam ja glup pa nemogu nać u bilježnici, ak ima još neko poput mene, ima dobrih primjera
http://en.wikipedia.org/wiki/Linear_least_squares pod Computation, http://en.wikipedia.org/wiki/Cholesky_decomposition, http://en.wikipedia.org/wiki/QR_decomposition#Connection_to_a_determinant_or_a_product_of_eigenvalues,
http://en.wikipedia.org/wiki/Singular_value_decomposition
Ko bi reko da SVD stoji za to...
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 14:01 ned, 15. 4. 2007 Naslov: Postano: 14:01 ned, 15. 4. 2007 Naslov: |
    |
|
|
Evo još jedno malo poduže pitanje (prvo da napišem dokle sam došo)
Recimo da imamo zadano [latex]m[/latex] točaka u ravnini i želimo provući pravac koji ih najbolje aproksimira. Želim minimizirati funkciju [latex]f\left( {a,b} \right) = \sum\limits_{i = 1}^m {\left( {ax_i + b - y_i } \right)^2 }
[/latex], tražim [latex]\frac{{\partial f}}{{\partial a}} = \sum\limits_{i = 1}^m {2\left( {ax_i + b - y_i } \right)x_i } = 0[/latex] i [latex]\frac{{\partial f}}{{\partial b}} = \sum\limits_{i = 1}^m {2\left( {ax_i + b - y_i } \right)} = 0[/latex]. Matrično
[latex]\left[ {\begin{array}{*{20}c}
{\sum\limits_{i = 1}^m {x_i^2 } } & {\sum\limits_{i = 1}^m {x_i } } \\
{\sum\limits_{i = 1}^m {x_i } } & {\sum\limits_{i = 1}^m 1 } \\
\end{array}} \right]\left[ {\begin{array}{*{20}c}
a \\
b \\
\end{array}} \right] = \left[ {\begin{array}{*{20}c}
{\sum\limits_{i = 1}^m {x_i y_i } } \\
{\sum\limits_{i = 1}^m {y_i } } \\
\end{array}} \right][/latex].
Sada primjetim da ako uzmem [latex]A = \left[ {\begin{array}{*{20}c}
{x_1 } & 1 \\
\vdots & \vdots \\
{x_m } & 1 \\
\end{array}} \right][/latex] i [latex]y = \left[ {\begin{array}{*{20}c}
{y_1 } \\
\vdots \\
{y_m } \\
\end{array}} \right][/latex] da to mogu zapisati kao [latex]A^T Ax = A^T y[/latex].
Ako je [latex]A[/latex] punog stupčanog ranga, onda je [latex]A^T A[/latex] pozitivno definitna pa mogu napravit faktorizaciju Choleskog, stavit [latex]A^T y =b[/latex] i riješit [latex]R^T Rx = b[/latex].
Ak sam dobro shvatio, to je prvi način rješavanja, zanima me jel to samo u slučaju kad je [latex]A[/latex] punog stupčanog ranga i dal je u slučaju da je to zadovoljeno to najoptimalniji način rješavanja tog sustava?
Onda dalje, kad napiše da želimo minimizirati [latex]\left\| {Ax - b} \right\|_2[/latex] koristeći [latex]QR[/latex] faktorizaciju, šta je tu [latex]A[/latex], a šta [latex]b[/latex] (mislim na ovaj konkretan problem sa pravcem koji sam gore napisao)? To je valjda drugi način rješavanja.
Zadnje, jel trebamo znat napravit ovu Singular Value Decomposition?
Hvala Zvoni unaprijed, znam da nema vremena baš
Ne treba, skužio sam
Evo još jedno malo poduže pitanje (prvo da napišem dokle sam došo)
Recimo da imamo zadano  točaka u ravnini i želimo provući pravac koji ih najbolje aproksimira. Želim minimizirati funkciju točaka u ravnini i želimo provući pravac koji ih najbolje aproksimira. Želim minimizirati funkciju 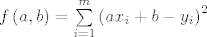 , tražim , tražim 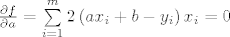 i i 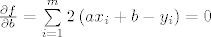 . Matrično . Matrično
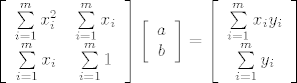 . .
Sada primjetim da ako uzmem 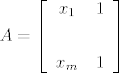 i i 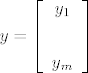 da to mogu zapisati kao da to mogu zapisati kao 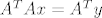 . .
Ako je  punog stupčanog ranga, onda je punog stupčanog ranga, onda je 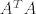 pozitivno definitna pa mogu napravit faktorizaciju Choleskog, stavit pozitivno definitna pa mogu napravit faktorizaciju Choleskog, stavit 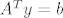 i riješit i riješit 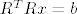 . .
Ak sam dobro shvatio, to je prvi način rješavanja, zanima me jel to samo u slučaju kad je  punog stupčanog ranga i dal je u slučaju da je to zadovoljeno to najoptimalniji način rješavanja tog sustava? punog stupčanog ranga i dal je u slučaju da je to zadovoljeno to najoptimalniji način rješavanja tog sustava?
Onda dalje, kad napiše da želimo minimizirati 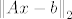 koristeći koristeći 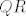 faktorizaciju, šta je tu faktorizaciju, šta je tu  , a šta , a šta 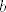 (mislim na ovaj konkretan problem sa pravcem koji sam gore napisao)? To je valjda drugi način rješavanja. (mislim na ovaj konkretan problem sa pravcem koji sam gore napisao)? To je valjda drugi način rješavanja.
Zadnje, jel trebamo znat napravit ovu Singular Value Decomposition?
Hvala Zvoni unaprijed, znam da nema vremena baš
Ne treba, skužio sam
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 19:31 ned, 15. 4. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
vedraf
Forumaš(ica)

Pridružen/a: 18. 09. 2006. (15:47:50)
Postovi: (BB)16
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
me_me
Forumaš(ica)

Pridružen/a: 10. 09. 2006. (11:56:01)
Postovi: (CC)16
|
|
| [Vrh] |
|
krafnica
Forumaš(ica)

Pridružen/a: 21. 09. 2006. (20:50:28)
Postovi: (5F)16
Spol: 
|
|
| [Vrh] |
|
me_me
Forumaš(ica)

Pridružen/a: 10. 09. 2006. (11:56:01)
Postovi: (CC)16
|
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
|











