| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 19:43 čet, 19. 4. 2007 Naslov: Postano: 19:43 čet, 19. 4. 2007 Naslov: |
    |
|
|
Kod ispitivanja gornje/donje trokutastosti ti nije bitna dijagonala. Tamo može biti bilo što. A u 3.11 ne broji jedinicu jer se ona for petlja sa k niti ne izvršava, a 1 po dogovoru i nije prost broj.
Kod ispitivanja gornje/donje trokutastosti ti nije bitna dijagonala. Tamo može biti bilo što. A u 3.11 ne broji jedinicu jer se ona for petlja sa k niti ne izvršava, a 1 po dogovoru i nije prost broj.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
marta
Forumaš(ica)

Pridružen/a: 15. 05. 2006. (14:27:19)
Postovi: (5F)16
Spol: 
|
|
| [Vrh] |
|
marta
Forumaš(ica)

Pridružen/a: 15. 05. 2006. (14:27:19)
Postovi: (5F)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:14 čet, 19. 4. 2007 Naslov: Re: zadaci s vježbi (par komentara) Postano: 21:14 čet, 19. 4. 2007 Naslov: Re: zadaci s vježbi (par komentara) |
    |
|
|
[quote="Blah"]Kada ispitujemo da li je broj prost u zadatku 3.11 zašto ne broji kad upišemo jedinicu?[/quote]
Od kad je 1 prost broj? :shock:
[quote="Blah"]Da li je gornje/donje trokutasta matrica samo onda kad su joj 0 iznad/ispod dijagonale jer u primjeru 3.1 se nula nalazi i u lijevom kutu a ne samo iznad dijagonale( aij!=0 za i<=j)[/quote]
Gradivo Linearne algebre. :P Definicija trokutastosti ne kaze da su nule [b]samo[/b] gore/dolje, nego da su gore/dolje nule, a s druge strane dijagonale bilo sto (pa mozda cak i nule). 8)
Zato i ona napomena da "ne trebate pisati da je matrica gornje i donje trokutasta ako je dijagonalna", jer je dijagonalna matrica stvarno i gornje i donje trokutasta. ;)
Zar vas nista ne uce na Elementarnoj i Linearnoj? :twisted: :P
| Blah (napisa): | | Kada ispitujemo da li je broj prost u zadatku 3.11 zašto ne broji kad upišemo jedinicu? |
Od kad je 1 prost broj? 
| Blah (napisa): | | Da li je gornje/donje trokutasta matrica samo onda kad su joj 0 iznad/ispod dijagonale jer u primjeru 3.1 se nula nalazi i u lijevom kutu a ne samo iznad dijagonale( aij!=0 za i⇐j) |
Gradivo Linearne algebre.  Definicija trokutastosti ne kaze da su nule samo gore/dolje, nego da su gore/dolje nule, a s druge strane dijagonale bilo sto (pa mozda cak i nule). Definicija trokutastosti ne kaze da su nule samo gore/dolje, nego da su gore/dolje nule, a s druge strane dijagonale bilo sto (pa mozda cak i nule). 
Zato i ona napomena da "ne trebate pisati da je matrica gornje i donje trokutasta ako je dijagonalna", jer je dijagonalna matrica stvarno i gornje i donje trokutasta. 
Zar vas nista ne uce na Elementarnoj i Linearnoj?  
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:47 čet, 19. 4. 2007 Naslov: Postano: 21:47 čet, 19. 4. 2007 Naslov: |
    |
|
|
[quote="Blah"]Zbunilo me to jer u gradivu uur-a koje sam probavala,jer nisam slušala lani,kad se ispituje da li je broj prost,kad upišeš 1 ispiše da je prost.[/quote]
Mozda je bila neka greska. :neznam: Ja sam uvijek naglasavao da jedan nije prost, bas zato jer je to bila cesta greska na pismenima. :?
[quote="Luuka"]@vsego Kad je već spomenut zadatak kad se ispituju svojstva matrice, bilo bi dobro da se u iduću verziju vježbi stavi i slučaj da je učitana matrica nul-matrica. Po ovom je ta matrica dijagonalna, što i jest u teoriji, ali ipak je malo glupo za nul matricu reć da je takva :roll:[/quote]
Nije glupo jer je to definicija. :? Kao da kazes da je glupo reci da je 2 paran jer parnost znaci "djeljivost s dva". :) Jednostavno, to je definicija i nul-matrica [b]je[/b] specijalni slucaj dijagonalne matrice, koja je specijalni slucaj i gornje i donje trokutaste matrice, kao i specijalni slucaj simetricne matrice. :D
Zato je i dana [b]matematicka[/b] definicija. 8) U cijeloj prici, bitnije je da znate provjeriti svojstvo zadano matematickom definicijom. ;) Recimo, ja sada definiram "resetkastu" matricu [latex]A \in \mathbb{R}^{m \times n}[/latex] kao matricu za koju vrijedi:
1. [latex]m, n \in 2\mathbb{N}_0 + 1[/latex] (dakle, [i]m[/i] i [i]n[/i] neparni) i
2. [latex]i, j \in 2 \mathbb{N} \Rightarrow A_{i,j} = 0[/latex]
Dakle, matrica koja na mjestu [latex]A_{i,j}[/latex] ima nule za sve parne [i]i[/i] i [i]j[/i] (pri tome nista ne kazem za neparne ili one razlicite parnosti ;)). Tada je opet nul-matrica neparnog reda "resetkasta". 8)
Naravno, u C-u indexi krecu od 0 (a ne od 1 kao u matematici), pa se definicija malo mijenja (gledaju se neparni [i]i[/i] i [i]j[/i]). ;)
Vidis, ja sam pojam "resetkaste" matrice sada izmislio i solidno sam siguran da se nigdje ne koristi jer mi djeluje solidno beskorisno. 8) Ali, dao sam matematicku definiciju i vi bi prema tome trebali znati provjeriti je li dana matrica "resetkasta". :D
Jasnije? ;)
P.S. Vidis... dobar zadatak za buducnost. :blista:
| Blah (napisa): | | Zbunilo me to jer u gradivu uur-a koje sam probavala,jer nisam slušala lani,kad se ispituje da li je broj prost,kad upišeš 1 ispiše da je prost. |
Mozda je bila neka greska.  Ja sam uvijek naglasavao da jedan nije prost, bas zato jer je to bila cesta greska na pismenima. Ja sam uvijek naglasavao da jedan nije prost, bas zato jer je to bila cesta greska na pismenima. 
| Luuka (napisa): | @vsego Kad je već spomenut zadatak kad se ispituju svojstva matrice, bilo bi dobro da se u iduću verziju vježbi stavi i slučaj da je učitana matrica nul-matrica. Po ovom je ta matrica dijagonalna, što i jest u teoriji, ali ipak je malo glupo za nul matricu reć da je takva  |
Nije glupo jer je to definicija.  Kao da kazes da je glupo reci da je 2 paran jer parnost znaci "djeljivost s dva". Kao da kazes da je glupo reci da je 2 paran jer parnost znaci "djeljivost s dva".  Jednostavno, to je definicija i nul-matrica je specijalni slucaj dijagonalne matrice, koja je specijalni slucaj i gornje i donje trokutaste matrice, kao i specijalni slucaj simetricne matrice. Jednostavno, to je definicija i nul-matrica je specijalni slucaj dijagonalne matrice, koja je specijalni slucaj i gornje i donje trokutaste matrice, kao i specijalni slucaj simetricne matrice. 
Zato je i dana matematicka definicija.  U cijeloj prici, bitnije je da znate provjeriti svojstvo zadano matematickom definicijom. U cijeloj prici, bitnije je da znate provjeriti svojstvo zadano matematickom definicijom.  Recimo, ja sada definiram "resetkastu" matricu Recimo, ja sada definiram "resetkastu" matricu 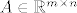 kao matricu za koju vrijedi: kao matricu za koju vrijedi:
1. 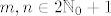 (dakle, m i n neparni) i (dakle, m i n neparni) i
2. 
Dakle, matrica koja na mjestu 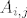 ima nule za sve parne i i j (pri tome nista ne kazem za neparne ili one razlicite parnosti ima nule za sve parne i i j (pri tome nista ne kazem za neparne ili one razlicite parnosti  ). Tada je opet nul-matrica neparnog reda "resetkasta". ). Tada je opet nul-matrica neparnog reda "resetkasta". 
Naravno, u C-u indexi krecu od 0 (a ne od 1 kao u matematici), pa se definicija malo mijenja (gledaju se neparni i i j). 
Vidis, ja sam pojam "resetkaste" matrice sada izmislio i solidno sam siguran da se nigdje ne koristi jer mi djeluje solidno beskorisno.  Ali, dao sam matematicku definiciju i vi bi prema tome trebali znati provjeriti je li dana matrica "resetkasta". Ali, dao sam matematicku definiciju i vi bi prema tome trebali znati provjeriti je li dana matrica "resetkasta". 
Jasnije? 
P.S. Vidis... dobar zadatak za buducnost. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
me_me
Forumaš(ica)

Pridružen/a: 10. 09. 2006. (11:56:01)
Postovi: (CC)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:54 čet, 19. 4. 2007 Naslov: Postano: 21:54 čet, 19. 4. 2007 Naslov: |
    |
|
|
[quote="me_me"][quote="Luuka"]@vsego Kad je već spomenut zadatak kad se ispituju svojstva matrice, bilo bi dobro da se u iduću verziju vježbi stavi i slučaj da je učitana matrica nul-matrica. Po ovom je ta matrica dijagonalna, što i jest u teoriji, ali ipak je malo glupo za nul matricu reć da je takva :roll:[/quote]
Nece ici, ajde procitaj tekst zadatka prije nego prodikujes. Lijepo je postavljen uvjet za dijagonalnu da je a[i][j] razlicito od nule za i=j. A ako nul matrica ima na dijagonali elemente razlite od nule onda mora da mi se jako pobrkalo gradivo linearne. :roll:[/quote]
Dijagonalna matrica nije ona koja ima ne-nule na dijagonali, nego ona koja ima nule izvan dijagonale. :|
Dakle, kako pise: [latex]a_{i,j} \not= 0 \Rightarrow i=j[/latex]
Ono sto ti pricas je obratno: [latex]i=j \Rightarrow a_{i,j} \not= 0[/latex]
Vidis razliku? ;)
| me_me (napisa): | | Luuka (napisa): | @vsego Kad je već spomenut zadatak kad se ispituju svojstva matrice, bilo bi dobro da se u iduću verziju vježbi stavi i slučaj da je učitana matrica nul-matrica. Po ovom je ta matrica dijagonalna, što i jest u teoriji, ali ipak je malo glupo za nul matricu reć da je takva  |
Nece ici, ajde procitaj tekst zadatka prije nego prodikujes. Lijepo je postavljen uvjet za dijagonalnu da je a[i][j] razlicito od nule za i=j. A ako nul matrica ima na dijagonali elemente razlite od nule onda mora da mi se jako pobrkalo gradivo linearne.  |
Dijagonalna matrica nije ona koja ima ne-nule na dijagonali, nego ona koja ima nule izvan dijagonale. 
Dakle, kako pise: 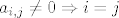
Ono sto ti pricas je obratno: 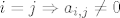
Vidis razliku? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
me_me
Forumaš(ica)

Pridružen/a: 10. 09. 2006. (11:56:01)
Postovi: (CC)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 23:43 čet, 19. 4. 2007 Naslov: Postano: 23:43 čet, 19. 4. 2007 Naslov: |
    |
|
|
[quote="ma"][quote="vsego"]Mozda je bila neka greska. :neznam:[/quote]
\:D/ [url=http://degiorgi.math.hr/forum/viewtopic.php?t=8733]da, da...[/url][/quote]
:grebgreb:
[quote="ma"][quote="vsego"]Vidis, ja sam pojam "resetkaste" matrice sada izmislio i solidno sam siguran da se nigdje ne koristi jer mi djeluje solidno beskorisno.[/quote]
meni je ideja odlična! pa one čine vektorski prostor :jabuka: . di ćeš boljeg svojstva? :woot:[/quote]
Cine li? :-k Cine grupu u odnosu na zbrajanje, ali nisu uopce zatvorene u odnosu na mnozenje. :?
[latex]M = \left[
\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}
\right] \Rightarrow M^2 = \left[
\begin{array}{lll}
3 & 2 & 3 \\
2 & 2 & 2 \\
3 & 2 & 3
\end{array}
\right][/latex]
@Luuka: bivanje vektorskim prostorom je korisno: lako se provjeri, a povlaci gomilu svojstava. ;)
| ma (napisa): | | vsego (napisa): | Mozda je bila neka greska.  |
 da, da... da, da... |

| ma (napisa): | | vsego (napisa): | | Vidis, ja sam pojam "resetkaste" matrice sada izmislio i solidno sam siguran da se nigdje ne koristi jer mi djeluje solidno beskorisno. |
meni je ideja odlična! pa one čine vektorski prostor  . di ćeš boljeg svojstva? . di ćeš boljeg svojstva?  |
Cine li?  Cine grupu u odnosu na zbrajanje, ali nisu uopce zatvorene u odnosu na mnozenje. Cine grupu u odnosu na zbrajanje, ali nisu uopce zatvorene u odnosu na mnozenje. 
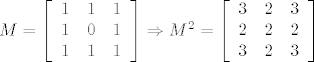
@Luuka: bivanje vektorskim prostorom je korisno: lako se provjeri, a povlaci gomilu svojstava. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 11:02 pet, 20. 4. 2007 Naslov: Postano: 11:02 pet, 20. 4. 2007 Naslov: |
    |
|
|
[quote="vsego"]Cine li? :-k Cine grupu u odnosu na zbrajanje, ali nisu uopce zatvorene u odnosu na mnozenje. :?
[latex]M = \left[
\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}
\right] \Rightarrow M^2 = \left[
\begin{array}{lll}
3 & 2 & 3 \\
2 & 2 & 2 \\
3 & 2 & 3
\end{array}
\right][/latex][/quote]
:ccc: čine, čine. bitno je zbrajanje i množenje skalarom.
da vrijedi ovo što si ti napisao, činile bi algebru. no, to ipak ne. :mracnjak:
Luuka, ako vektorske prostore ne smatraš važnima i korisnima, što misliš tek o kolegiju linearna 1? :lol:
[size=7]znam, znam, dijelim tvoje mišljenje...[/size] :crazyeyes:
| vsego (napisa): | Cine li?  Cine grupu u odnosu na zbrajanje, ali nisu uopce zatvorene u odnosu na mnozenje. Cine grupu u odnosu na zbrajanje, ali nisu uopce zatvorene u odnosu na mnozenje. 
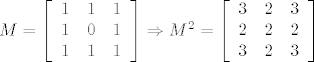 |
 čine, čine. bitno je zbrajanje i množenje skalarom. čine, čine. bitno je zbrajanje i množenje skalarom.
da vrijedi ovo što si ti napisao, činile bi algebru. no, to ipak ne. 
Luuka, ako vektorske prostore ne smatraš važnima i korisnima, što misliš tek o kolegiju linearna 1? 
znam, znam, dijelim tvoje mišljenje... 
_________________
ima let u finish
|
|
| [Vrh] |
|
|




















