| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 19:07 pet, 11. 5. 2007 Naslov: Hammingovi kodovi Postano: 19:07 pet, 11. 5. 2007 Naslov: Hammingovi kodovi |
    |
|
|
Kao sto sam dugo najavljivao (:lol:) donosim vam pricu o Hammingovim kodovima koja je vjesto zamaskirana u vjerojatnosni problem. Ne znam koliko cemo o tome raditi na predavanjima (buduci da nikada ne dolazim,ne svojom krivicom) no moglo bi biti veoma zanimljivo, te dobar uvod u Hammingove kodove ukoliko cemo o tome govoriti. Dakle,prica ide....
(neke rijeci cu namjerno ostaviti na engleskom jeziku, na kojem je izvorna prica,nadam se da nece smetati)
U intergalaktickom zatvoru sa [b]jako puno[/b] zatvorenika, upravitelj ih sve odluci sve rijesiti,tako da ih ili pogubi :cry: ili da ih sve oslobodi :D . Sljedeci dan svi zatvorenici su dovedeni u dvoriste zatvora te ce im cuvari na slucajan nacin stavljati bijele ili crne sesirice na glavu (nezavisno,sa vjeroj. 1/2) ,te ce svi zatvorenici moci vidjeti sve sesirice osim svojeg.Tada ce zatvorenici biti dovedeni u upraviteljev ured te ce biti pitani koje je boje njihov sesiric. Mogu reci: bijeli , crni ili ne znam. Nijedan zatvorenik nece znati odgovor od drugih zatvorenika. Ako svi zatvorenici kazu -ne znam- i barem jedan zatvorenik kaze egzaktan odgovor : -bijeli ses. - ili -crni- , te je odgovor krivi , svi ce biti pogubljeni. Ako barem jedan zatvorenik dade egzaktan odgovor ,te svi koji su dali egzatkan odgovor , su bili tocni su ce biti oslobodeni.
Na danasnji dan zatvorenicima je dopusteno da se sastanu i smisle strategiju koju zele, te je njihova zadaca da smisle strategiju koja dopusta da zatvorenici budu oslobodeni sa vjerojatnoscu barem [latex]0.999[/latex] .
Kao sto sam dugo najavljivao ( ) donosim vam pricu o Hammingovim kodovima koja je vjesto zamaskirana u vjerojatnosni problem. Ne znam koliko cemo o tome raditi na predavanjima (buduci da nikada ne dolazim,ne svojom krivicom) no moglo bi biti veoma zanimljivo, te dobar uvod u Hammingove kodove ukoliko cemo o tome govoriti. Dakle,prica ide.... ) donosim vam pricu o Hammingovim kodovima koja je vjesto zamaskirana u vjerojatnosni problem. Ne znam koliko cemo o tome raditi na predavanjima (buduci da nikada ne dolazim,ne svojom krivicom) no moglo bi biti veoma zanimljivo, te dobar uvod u Hammingove kodove ukoliko cemo o tome govoriti. Dakle,prica ide....
(neke rijeci cu namjerno ostaviti na engleskom jeziku, na kojem je izvorna prica,nadam se da nece smetati)
U intergalaktickom zatvoru sa jako puno zatvorenika, upravitelj ih sve odluci sve rijesiti,tako da ih ili pogubi  ili da ih sve oslobodi ili da ih sve oslobodi  . Sljedeci dan svi zatvorenici su dovedeni u dvoriste zatvora te ce im cuvari na slucajan nacin stavljati bijele ili crne sesirice na glavu (nezavisno,sa vjeroj. 1/2) ,te ce svi zatvorenici moci vidjeti sve sesirice osim svojeg.Tada ce zatvorenici biti dovedeni u upraviteljev ured te ce biti pitani koje je boje njihov sesiric. Mogu reci: bijeli , crni ili ne znam. Nijedan zatvorenik nece znati odgovor od drugih zatvorenika. Ako svi zatvorenici kazu -ne znam- i barem jedan zatvorenik kaze egzaktan odgovor : -bijeli ses. - ili -crni- , te je odgovor krivi , svi ce biti pogubljeni. Ako barem jedan zatvorenik dade egzaktan odgovor ,te svi koji su dali egzatkan odgovor , su bili tocni su ce biti oslobodeni. . Sljedeci dan svi zatvorenici su dovedeni u dvoriste zatvora te ce im cuvari na slucajan nacin stavljati bijele ili crne sesirice na glavu (nezavisno,sa vjeroj. 1/2) ,te ce svi zatvorenici moci vidjeti sve sesirice osim svojeg.Tada ce zatvorenici biti dovedeni u upraviteljev ured te ce biti pitani koje je boje njihov sesiric. Mogu reci: bijeli , crni ili ne znam. Nijedan zatvorenik nece znati odgovor od drugih zatvorenika. Ako svi zatvorenici kazu -ne znam- i barem jedan zatvorenik kaze egzaktan odgovor : -bijeli ses. - ili -crni- , te je odgovor krivi , svi ce biti pogubljeni. Ako barem jedan zatvorenik dade egzaktan odgovor ,te svi koji su dali egzatkan odgovor , su bili tocni su ce biti oslobodeni.
Na danasnji dan zatvorenicima je dopusteno da se sastanu i smisle strategiju koju zele, te je njihova zadaca da smisle strategiju koja dopusta da zatvorenici budu oslobodeni sa vjerojatnoscu barem 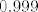 . .
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 19:07 pet, 11. 5. 2007 Naslov: Postano: 19:07 pet, 11. 5. 2007 Naslov: |
    |
|
|
Dakle,rjesenje ovisi o 'error correcting' kodovima , te moze biti pokazano da ako je [latex]n[/latex] zatvorenika da tada najbolja vjeroj. prezivljavanja [latex]\frac{n}{n+1}[/latex] te ce se gornja ograda postici za [latex]n=2^k - 1[/latex]. Evo i rjesenja
Definiramo slucajnu varijablu [latex] X_j[/latex] sa [latex]X_j=1[/latex] ako zatvorenik tocno odgovori [latex]X_j=-1[/latex] ako da krivi odgovor,te [latex]X_j=0[/latex] ako kaze -ne znam- . Odmah imamo da [latex]E[X_j]=0,\forall j[/latex],tj. [latex]E[\sum_{j=0}^n X_j]=0[/latex]
[latex]P(prezivljavanje)\leq P(\sum_j X_j >0)=P(\sum_j X_j \geq 1)[/latex].
Neka je [latex]Y=\sum_{j=0}^n X_j[/latex] i [latex]A:={Y\geq 1}[/latex],na [latex]A[/latex], [latex]Y \geq -n[/latex] na [latex]A^c[/latex].
[latex]0=E[Y]\geq 1\cdot P(A)-n(1-P(A))=(n+1)P(A)-n, P(A)\leq \frac{n}{n+1}[/latex] sto daj da vjerojatnost prezivljavanja ne prelazi [latex]\frac{n}{n+1}[/latex].
Neka je [latex]p(n)[/latex] optimizirana vjeroj. sa n sudionika.Imamo tri stvari da je [latex]p(n)[/latex] je neopadajuca funkcija ( tj ako imamo strategiju koja postize p(n) te ako dodamo jos jednog sudionika tada on jednostavno kaze -ne znam- te ostali provode prije dogovorenu strategiju) ,dalje gornja granica je [latex]\frac{n}{n+1}[/latex], te da se gornja granica postize za [latex]n=2^k-1[/latex] (tj. to je 'savrsen kod' ).Te,sada dolazi dugo najavljivana konstrukcija Hammingovih kodova..
Dakle,rjesenje ovisi o 'error correcting' kodovima , te moze biti pokazano da ako je  zatvorenika da tada najbolja vjeroj. prezivljavanja zatvorenika da tada najbolja vjeroj. prezivljavanja 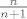 te ce se gornja ograda postici za te ce se gornja ograda postici za 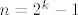 . Evo i rjesenja . Evo i rjesenja
Definiramo slucajnu varijablu 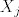 sa sa 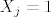 ako zatvorenik tocno odgovori ako zatvorenik tocno odgovori  ako da krivi odgovor,te ako da krivi odgovor,te 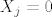 ako kaze -ne znam- . Odmah imamo da ako kaze -ne znam- . Odmah imamo da 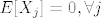 ,tj. ,tj. 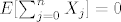
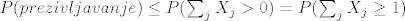 . .
Neka je 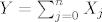 i i 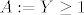 ,na ,na  , ,  na na 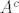 . .
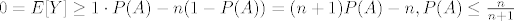 sto daj da vjerojatnost prezivljavanja ne prelazi sto daj da vjerojatnost prezivljavanja ne prelazi 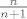 . .
Neka je 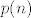 optimizirana vjeroj. sa n sudionika.Imamo tri stvari da je optimizirana vjeroj. sa n sudionika.Imamo tri stvari da je 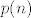 je neopadajuca funkcija ( tj ako imamo strategiju koja postize p(n) te ako dodamo jos jednog sudionika tada on jednostavno kaze -ne znam- te ostali provode prije dogovorenu strategiju) ,dalje gornja granica je je neopadajuca funkcija ( tj ako imamo strategiju koja postize p(n) te ako dodamo jos jednog sudionika tada on jednostavno kaze -ne znam- te ostali provode prije dogovorenu strategiju) ,dalje gornja granica je 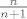 , te da se gornja granica postize za , te da se gornja granica postize za 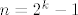 (tj. to je 'savrsen kod' ).Te,sada dolazi dugo najavljivana konstrukcija Hammingovih kodova.. (tj. to je 'savrsen kod' ).Te,sada dolazi dugo najavljivana konstrukcija Hammingovih kodova..
Zadnja promjena: Mr.Doe; 19:12 pet, 11. 5. 2007; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 19:08 pet, 11. 5. 2007 Naslov: Postano: 19:08 pet, 11. 5. 2007 Naslov: |
    |
|
|
Da bi kreirali kod za [latex]n=2^k -1[/latex], neka je M [latex]k\times (2^k -1)[/latex] matrica cije se stupci sastoje od svih [latex]2^k -1[/latex] mogucih vektora u [latex](\mathbb{Z}_2)^n[/latex]. Skup kodova je sada nul prostor od te matrice .Buduci da je rang matrice [latex]2^k - k-1[/latex] i ima [latex]2^{2^k-k-1}[/latex] elemenata. Imamo jednostavan algoritam za dekodiranje: poredamo stupce matrice M u pretku binarni razvoja brojeva [latex]\{1,2,\dots , 2^k -1\}[/latex]. Za danu rijec[latex]x[/latex],sada vektor stupac izracunamo [latex]Mx[/latex]. Ako je [latex]Mx=0[/latex] tada je x kodna rijec . Ako je [latex]Mx=y[/latex] tada je [latex]y[/latex] binarni razvoj broja [latex]q[/latex] .Promijenio [latex]q[/latex]-ti bit od x da dobijemo najblizu kodnu rijec.
Koliko mi je poznato prica je bila u New York Timesu prije par godina no nije dano rijesnje (dakako nisam ga ni ja dao :D)
Nadam se da ste uzivali u prici, te da ce to biti dobar uvod u Hammingove kodove. Krcko, ukoliko ti je nesta od ovog poznato,samo vici !
Da bi kreirali kod za 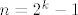 , neka je M , neka je M 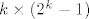 matrica cije se stupci sastoje od svih matrica cije se stupci sastoje od svih 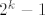 mogucih vektora u mogucih vektora u 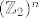 . Skup kodova je sada nul prostor od te matrice .Buduci da je rang matrice . Skup kodova je sada nul prostor od te matrice .Buduci da je rang matrice 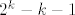 i ima i ima 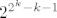 elemenata. Imamo jednostavan algoritam za dekodiranje: poredamo stupce matrice M u pretku binarni razvoja brojeva elemenata. Imamo jednostavan algoritam za dekodiranje: poredamo stupce matrice M u pretku binarni razvoja brojeva 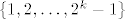 . Za danu rijec . Za danu rijec ,sada vektor stupac izracunamo ,sada vektor stupac izracunamo 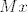 . Ako je . Ako je 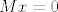 tada je x kodna rijec . Ako je tada je x kodna rijec . Ako je 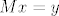 tada je tada je  binarni razvoj broja binarni razvoj broja  .Promijenio .Promijenio  -ti bit od x da dobijemo najblizu kodnu rijec. -ti bit od x da dobijemo najblizu kodnu rijec.
Koliko mi je poznato prica je bila u New York Timesu prije par godina no nije dano rijesnje (dakako nisam ga ni ja dao  ) )
Nadam se da ste uzivali u prici, te da ce to biti dobar uvod u Hammingove kodove. Krcko, ukoliko ti je nesta od ovog poznato,samo vici !
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|




