| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
c_l
Forumaš(ica)


Pridružen/a: 01. 02. 2007. (12:28:28)
Postovi: (98)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
c_l
Forumaš(ica)


Pridružen/a: 01. 02. 2007. (12:28:28)
Postovi: (98)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
c_l
Forumaš(ica)


Pridružen/a: 01. 02. 2007. (12:28:28)
Postovi: (98)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
 Postano: 9:42 pet, 22. 6. 2007 Naslov: Postano: 9:42 pet, 22. 6. 2007 Naslov: |
    |
|
|
Na internetu sam nasao jedan primjer koji se temelji na zapisu realanog broja u verizni razlomak, ali bez dokaza. Dokaz da takav postoji je puno laksi od konstrukcije ide ovako Borelovih skupova ima kontunuum, a Lebesgovih ima 2^kontunuum.
Dokaz
Cantorov skup je neprebrojiv i Lebesgov pa su i svi njegovi postskupovi Lebesgouvi jer je Lebesgova mjera potpuna pa ih ima 2^kontunuum, a buduci da Lebesgovih skupova ima najvise 2^kontinuum sto je kardinalni broj od partitivnog skupa skupa realnih brojeva vidimo da Lebesgovih skupova ima 2^kontunuum.
S druge strane napravimo ovakvu konstrukciju Borelovih skupova: prvo uzmimo samo otvorene intervale I1 ima ih kontunuum pa napravimo sve prebrojive ili konacne unije otvorenih intervala I2 tih ima kontunuum^alef0=kontunuum zatim uzmimo razlike svaka dva elementa iz I2 tako dobimo I3, sada opet uzmemo sve prebrojive ili konacne unije elemenata iz I3, pa dobijemo I4,... u svakom koraku povecamo skup ali kardinalnost ostaje kontunuum tim postupkom ocito dobijemo sve Borelove skupove. kojih onda ime manje nego kontinuum^alef0=kontunuum.
Pa sigurno postoji skup koji je Lebegov, a nje Borelov.
Na internetu sam nasao jedan primjer koji se temelji na zapisu realanog broja u verizni razlomak, ali bez dokaza. Dokaz da takav postoji je puno laksi od konstrukcije ide ovako Borelovih skupova ima kontunuum, a Lebesgovih ima 2^kontunuum.
Dokaz
Cantorov skup je neprebrojiv i Lebesgov pa su i svi njegovi postskupovi Lebesgouvi jer je Lebesgova mjera potpuna pa ih ima 2^kontunuum, a buduci da Lebesgovih skupova ima najvise 2^kontinuum sto je kardinalni broj od partitivnog skupa skupa realnih brojeva vidimo da Lebesgovih skupova ima 2^kontunuum.
S druge strane napravimo ovakvu konstrukciju Borelovih skupova: prvo uzmimo samo otvorene intervale I1 ima ih kontunuum pa napravimo sve prebrojive ili konacne unije otvorenih intervala I2 tih ima kontunuum^alef0=kontunuum zatim uzmimo razlike svaka dva elementa iz I2 tako dobimo I3, sada opet uzmemo sve prebrojive ili konacne unije elemenata iz I3, pa dobijemo I4,... u svakom koraku povecamo skup ali kardinalnost ostaje kontunuum tim postupkom ocito dobijemo sve Borelove skupove. kojih onda ime manje nego kontinuum^alef0=kontunuum.
Pa sigurno postoji skup koji je Lebegov, a nje Borelov.
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 18:11 sub, 23. 6. 2007 Naslov: Postano: 18:11 sub, 23. 6. 2007 Naslov: |
    |
|
|
14. pitanje: Istina. A kako se dokaže za nenegativne? :grebgreb:
[quote]Za mjeru kazemo da je potpuna ako je pripadni prostor s mjerom potpun? [/quote]
Ja sam to tako shvatio.
4. pitanje: Da, zapravo sam ga ja tako rješavao.
24. : Mislim da da.
25. : Da, ali šta bi tu trebalo dokazati? One aksiome iz alternativne definicije? I opet je definirana na prstenu, a ne algebri :?
Primjer mjere koja nije sigma-konačna:
Neka je [latex]+\infty[/latex] u nepraznim skupovima i 0 na praznom skupu. Uzmi bilo koji izmjeriv prostor.
Imam i ja neka pitanja:
3. Koji su razlozi da su nam svojstva koja zahtijevamo od Lebesgue-ove mjere zadovoljavajuća? Mislim, padaju mi na pamet samo oni, "intuitivnosti radi" razlozi...
14. Ummm, primjer metričkog koji nije normiran? :oops: Malo me sram, možda bi i smislio da se ubijem or razmišljanja al čini mi se da će oni koji su slušali metričke prije znati.
23. Ovo ne vrijedi za proizvoljnu familiju C. Npr [latex]C=\{\{a\},\{a,b\}\}[/latex] i [latex]A=\{\emptyset,\{a\},\{a,b\}\}[/latex] a to nije prsten jer [latex]\{a,b\}\backslash \{a\}=\{b\}\notin A[/latex]
Možda je profesor mislio na poluprsten?
14. pitanje: Istina. A kako se dokaže za nenegativne? 
| Citat: | | Za mjeru kazemo da je potpuna ako je pripadni prostor s mjerom potpun? |
Ja sam to tako shvatio.
4. pitanje: Da, zapravo sam ga ja tako rješavao.
24. : Mislim da da.
25. : Da, ali šta bi tu trebalo dokazati? One aksiome iz alternativne definicije? I opet je definirana na prstenu, a ne algebri 
Primjer mjere koja nije sigma-konačna:
Neka je  u nepraznim skupovima i 0 na praznom skupu. Uzmi bilo koji izmjeriv prostor. u nepraznim skupovima i 0 na praznom skupu. Uzmi bilo koji izmjeriv prostor.
Imam i ja neka pitanja:
3. Koji su razlozi da su nam svojstva koja zahtijevamo od Lebesgue-ove mjere zadovoljavajuća? Mislim, padaju mi na pamet samo oni, "intuitivnosti radi" razlozi...
14. Ummm, primjer metričkog koji nije normiran?  Malo me sram, možda bi i smislio da se ubijem or razmišljanja al čini mi se da će oni koji su slušali metričke prije znati. Malo me sram, možda bi i smislio da se ubijem or razmišljanja al čini mi se da će oni koji su slušali metričke prije znati.
23. Ovo ne vrijedi za proizvoljnu familiju C. Npr 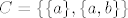 i i 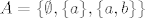 a to nije prsten jer a to nije prsten jer 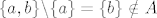
Možda je profesor mislio na poluprsten?
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 18:33 sub, 23. 6. 2007 Naslov: Postano: 18:33 sub, 23. 6. 2007 Naslov: |
    |
|
|
[latex](X,\mathcal{M})=([0,1],\mathcal{B}([0,1])),\mu : \mathcal{M}\rightarrow \mathbb{R} \cup \{-\infty,+\infty\}[/latex]. def. je sa
[latex]\mu (A):=card(\mathbb{R}\backslash \mathbb{Q} \cap A) [/latex], ako [latex]card(\mathbb{R}\backslash \mathbb{Q}\cap A)\in \mathbb{N}\cup \{0 \}[/latex], inace [latex]+\infty[/latex].
Moze se pokazati da je mjera ,no nije [latex] \sigma [/latex] konacna.
(mozete primjetiti da sam "malo" modificirao jedan od zadataka sa kolokvija 8) , takoder postoji mogucnost da sam "bubnuo" glupost ,buduci da sada ne ucim integral i mjeru, te unaprijed uvazite moje isprike )
Edit:
Takoder je nepotrebno, definirati je na R (potez) ,buduci da je ocito nenegativna
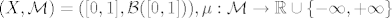 . def. je sa . def. je sa
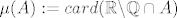 , ako , ako 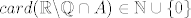 , inace , inace  . .
Moze se pokazati da je mjera ,no nije  konacna. konacna.
(mozete primjetiti da sam "malo" modificirao jedan od zadataka sa kolokvija  , takoder postoji mogucnost da sam "bubnuo" glupost ,buduci da sada ne ucim integral i mjeru, te unaprijed uvazite moje isprike ) , takoder postoji mogucnost da sam "bubnuo" glupost ,buduci da sada ne ucim integral i mjeru, te unaprijed uvazite moje isprike )
Edit:
Takoder je nepotrebno, definirati je na R (potez) ,buduci da je ocito nenegativna
|
|
| [Vrh] |
|
|












