| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:12 uto, 19. 6. 2007 Naslov: Postano: 13:12 uto, 19. 6. 2007 Naslov: |
    |
|
|
Može se jednostavnije ovako.
Neka je npr (x,y,z,t) neki od preostalih traženih vektora (stupaca,
lakše je ovako pisati). Iz uvjeta ortogonalnosti na prva dva vektora
imamo:
x = z, y = t (vrlo lagani račun).
Sad za treći vektor, uzimajući u obzir da je jedinični, možemo izabrati
npr.
(1/2, 1/2, 1/2, 1/2),
a onda je lako naći i četvrti vektor.
Može se jednostavnije ovako.
Neka je npr (x,y,z,t) neki od preostalih traženih vektora (stupaca,
lakše je ovako pisati). Iz uvjeta ortogonalnosti na prva dva vektora
imamo:
x = z, y = t (vrlo lagani račun).
Sad za treći vektor, uzimajući u obzir da je jedinični, možemo izabrati
npr.
(1/2, 1/2, 1/2, 1/2),
a onda je lako naći i četvrti vektor.
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 21:20 čet, 21. 6. 2007 Naslov: Postano: 21:20 čet, 21. 6. 2007 Naslov: |
    |
|
|
[quote="5ra"]evo nadovezujem se na temu jer imam jedno pitanje. U trecem zadatku iz zadaće traži se ortogonalna projekcija na M,pa me zanima treba li bazu za M ortonormirati ili ne?[/quote]
Treba, jer je [latex]P(v) = \sum_{i=1}^k (v|e_{i})e_{i}[/latex] , gdje je {e1, ..., ek} ortonormirana baza za potprostor M, takva je bar definicija ortogonalnog projektora P s predavanja.
| 5ra (napisa): | | evo nadovezujem se na temu jer imam jedno pitanje. U trecem zadatku iz zadaće traži se ortogonalna projekcija na M,pa me zanima treba li bazu za M ortonormirati ili ne? |
Treba, jer je 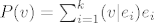 , gdje je {e1, ..., ek} ortonormirana baza za potprostor M, takva je bar definicija ortogonalnog projektora P s predavanja. , gdje je {e1, ..., ek} ortonormirana baza za potprostor M, takva je bar definicija ortogonalnog projektora P s predavanja.
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 14:10 pet, 22. 6. 2007 Naslov: Postano: 14:10 pet, 22. 6. 2007 Naslov: |
    |
|
|
Ne, bazu za M nije potrebno ortonormirati u ovom slučaju, ali je istina da je općenito za traženje orotogonalne projekcije najpraktičnije ortonormirati bazu zadanog potprostora.
Što se tiče definicije projektora, nemojmo miješati definiciju i metodu izračunavanja. Formula je točna, ali definicija ne ovisi o bazi.
U konkretnom zadatku, očito je ortogonalni komplement zadan vektorom (1,-2,2) (to su koeficijenti jednadžbe ravnine koja je zapravo naš potprostor M), a bazu potprostora očito čine (2,1,0) i (-2,0,1). Vektori nisu ortogonalni, ali to ovdje nije ni bitno, jer trebamo napisati zadani vektor (1,2,2) kao linearnu kombinaciju
a(2,1,0) + b(-2,0,1) + c(1,-2,2), a rješava se, dakako, sustav od 3 jednadžbe s 3 nepoznanice i tražena ortogonalna projekcija je onda
a(2,1,0) + b(-2,0,1) = (4/9) (2,5,4).
Dakle, koristili smo samo ortogonalnost, bez normiranja i bez ortonormirane baze. Jasno, dobra je vježba načiniti to i pomoću orotonormirane baze i primijeniti formulu, ali važno je i razumijeti što se točno radi i bez gotovoh formula.
Ne, bazu za M nije potrebno ortonormirati u ovom slučaju, ali je istina da je općenito za traženje orotogonalne projekcije najpraktičnije ortonormirati bazu zadanog potprostora.
Što se tiče definicije projektora, nemojmo miješati definiciju i metodu izračunavanja. Formula je točna, ali definicija ne ovisi o bazi.
U konkretnom zadatku, očito je ortogonalni komplement zadan vektorom (1,-2,2) (to su koeficijenti jednadžbe ravnine koja je zapravo naš potprostor M), a bazu potprostora očito čine (2,1,0) i (-2,0,1). Vektori nisu ortogonalni, ali to ovdje nije ni bitno, jer trebamo napisati zadani vektor (1,2,2) kao linearnu kombinaciju
a(2,1,0) + b(-2,0,1) + c(1,-2,2), a rješava se, dakako, sustav od 3 jednadžbe s 3 nepoznanice i tražena ortogonalna projekcija je onda
a(2,1,0) + b(-2,0,1) = (4/9) (2,5,4).
Dakle, koristili smo samo ortogonalnost, bez normiranja i bez ortonormirane baze. Jasno, dobra je vježba načiniti to i pomoću orotonormirane baze i primijeniti formulu, ali važno je i razumijeti što se točno radi i bez gotovoh formula.
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 15:02 pet, 22. 6. 2007 Naslov: Postano: 15:02 pet, 22. 6. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Ne, bazu za M nije potrebno ortonormirati u ovom slučaju, ali je istina da je općenito za traženje orotogonalne projekcije najpraktičnije ortonormirati bazu zadanog potprostora.
Što se tiče definicije projektora, nemojmo miješati definiciju i metodu izračunavanja. Formula je točna, ali definicija ne ovisi o bazi.
U konkretnom zadatku, očito je ortogonalni komplement zadan vektorom (1,-2,2) (to su koeficijenti jednadžbe ravnine koja je zapravo naš potprostor M), a bazu potprostora očito čine (2,1,0) i (-2,0,1). Vektori nisu ortogonalni, ali to ovdje nije ni bitno, jer trebamo napisati zadani vektor (1,2,2) kao linearnu kombinaciju
a(2,1,0) + b(-2,0,1) + c(1,-2,2), a rješava se, dakako, sustav od 3 jednadžbe s 3 nepoznanice i tražena ortogonalna projekcija je onda
a(2,1,0) + b(-2,0,1) = (4/9) (2,5,4).
Dakle, koristili smo samo ortogonalnost, bez normiranja i bez ortonormirane baze. Jasno, dobra je vježba načiniti to i pomoću orotonormirane baze i primijeniti formulu, ali važno je i razumijeti što se točno radi i bez gotovoh formula.[/quote]
Istina, ovo je "lakši" način zapravo. Hvala! :wink:
| Anonymous (napisa): | Ne, bazu za M nije potrebno ortonormirati u ovom slučaju, ali je istina da je općenito za traženje orotogonalne projekcije najpraktičnije ortonormirati bazu zadanog potprostora.
Što se tiče definicije projektora, nemojmo miješati definiciju i metodu izračunavanja. Formula je točna, ali definicija ne ovisi o bazi.
U konkretnom zadatku, očito je ortogonalni komplement zadan vektorom (1,-2,2) (to su koeficijenti jednadžbe ravnine koja je zapravo naš potprostor M), a bazu potprostora očito čine (2,1,0) i (-2,0,1). Vektori nisu ortogonalni, ali to ovdje nije ni bitno, jer trebamo napisati zadani vektor (1,2,2) kao linearnu kombinaciju
a(2,1,0) + b(-2,0,1) + c(1,-2,2), a rješava se, dakako, sustav od 3 jednadžbe s 3 nepoznanice i tražena ortogonalna projekcija je onda
a(2,1,0) + b(-2,0,1) = (4/9) (2,5,4).
Dakle, koristili smo samo ortogonalnost, bez normiranja i bez ortonormirane baze. Jasno, dobra je vježba načiniti to i pomoću orotonormirane baze i primijeniti formulu, ali važno je i razumijeti što se točno radi i bez gotovoh formula. |
Istina, ovo je "lakši" način zapravo. Hvala! 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
rhiannon
Forumaš(ica)

Pridružen/a: 11. 06. 2007. (20:34:03)
Postovi: (D)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 11:10 pon, 25. 6. 2007 Naslov: Postano: 11:10 pon, 25. 6. 2007 Naslov: |
    |
|
|
jel onda igra neku ulogu ona 1/2 ispred matrice? Ili se traži ort komplement prostora razapetih sa prva 2 stupca pa se onda to normira i onda kad se napiše ta matrica (ona 4x4) sa 1/2 naprijed sve štima?
jel onda igra neku ulogu ona 1/2 ispred matrice? Ili se traži ort komplement prostora razapetih sa prva 2 stupca pa se onda to normira i onda kad se napiše ta matrica (ona 4x4) sa 1/2 naprijed sve štima?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
woodstock
Forumaš(ica)


Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol: 
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 12:39 pon, 25. 6. 2007 Naslov: Postano: 12:39 pon, 25. 6. 2007 Naslov: |
    |
|
|
[quote="woodstock"]Može li netko postati konačnu matricu? Please :roll:[/quote]
Pre ljen sam, al u postu #6 ti je apsolutno sve objašnjeno, i postupak je pljuga. 8)
Pitanjce vezano uz pitanje iz zadaće (zadnje) - da li se svaka matrica A iz Mkn, gdje je k < n ciji stupci su ortonormirani moze nadopuniti do unitarne matrice Mn? E sad, to je malo "obrnuta situacija" nego ona iz samog zadatka, jer imamo broj stupaca početne matrice strogo veći od broja redaka, i znamo da su ti stupci ortonormirani, ali ne znam kako to utječe na retke? Odnosno, kad bi iz tog proizašlo da je i tih k redaka ortonormirano, tada se sigurno može nadopuniti (po retcima) do unitarne matrice Mn !
| woodstock (napisa): | Može li netko postati konačnu matricu? Please  |
Pre ljen sam, al u postu #6 ti je apsolutno sve objašnjeno, i postupak je pljuga. 
Pitanjce vezano uz pitanje iz zadaće (zadnje) - da li se svaka matrica A iz Mkn, gdje je k < n ciji stupci su ortonormirani moze nadopuniti do unitarne matrice Mn? E sad, to je malo "obrnuta situacija" nego ona iz samog zadatka, jer imamo broj stupaca početne matrice strogo veći od broja redaka, i znamo da su ti stupci ortonormirani, ali ne znam kako to utječe na retke? Odnosno, kad bi iz tog proizašlo da je i tih k redaka ortonormirano, tada se sigurno može nadopuniti (po retcima) do unitarne matrice Mn !
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
rhiannon
Forumaš(ica)

Pridružen/a: 11. 06. 2007. (20:34:03)
Postovi: (D)16
|
|
| [Vrh] |
|
|












