| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
 Postano: 21:21 pon, 10. 9. 2007 Naslov: sup inf i lema 7.1 Postano: 21:21 pon, 10. 9. 2007 Naslov: sup inf i lema 7.1 |
    |
|
|
Pozdrav.
Kaze lema 7.1:
[code:1]Funkcija f: A->R je neprekidna u c € A akko je O(f,c)=0.[/code:1]
Dokaz kaze ovako (smjer [latex]\Rightarrow[/latex]):
Pretpostavimo da je f neprekidna u c. Tada za svaki [latex]\epsilon>0[/latex] postoji [latex]U\ni c[/latex] t.d. za [latex]x\in U \Rightarrow |f(x)-f(c)|<\frac{\epsilon}{2}[/latex]
Za [latex]x_{1}, x_{2} \in U \Rightarrow |f(x_{1})-f(x_{2})|<\epsilon[/latex].
Sllijedi da je [latex]\displaystyle\formula \sup_{x_{1}, x_{2} \in U} |f(x_{1})-f(x_{2})|\le \epsilon[/latex]
Slijedi [latex]O(f,c)\le\epsilon[/latex].
[latex]\epsilon[/latex] je proizvoljan [latex]\Rightarrow O(f,c)=0[/latex]
QED
Meni nikako nije jasno kako smo oscilaciju uveli u igru, tj. kako iz [latex]\displaystyle\formula \sup_{x_{1}, x_{2} \in U} |f(x_{1})-f(x_{2})|\le \epsilon[/latex] slijedi [latex]O(f,c)\le\epsilon[/latex].
Oscilacija je definirana kao [latex]\displaystyle\formula \sup_{U\ni c} \inf_{x_{1}, x_{2} \in U} |f(x_{1})-f(x_{2})|[/latex].
To ja shvacam tako da u vanjskoj petlji (supremum) trazimo okolinu s najvecim minimumom; tj. okolinu u kojoj je [latex]\displaystyle\formula \inf_{x_{1}, x_{2} \in U} |f(x_{1})-f(x_{2})|[/latex] najveci, dakle okolinu u kojoj je minimum od [latex]|f(x_{1})-f(x_{2})|[/latex] najveci.
U dokazu imamo da za svaki [latex]\epsilon[/latex] postoji okolina [latex]U[/latex] t.d. je [latex]\displaystyle\formula \sup_{x_{1}, x_{2} \in U} |f(x_{1})-f(x_{2})|\le \epsilon[/latex], pa onda valjda posebno i [latex]\displaystyle\formula \inf_{x_{1}, x_{2} \in U} |f(x_{1})-f(x_{2})|\le \epsilon[/latex]. Dakle za svaki [latex]\epsilon[/latex] postoji okolina u kojoj je infinum ogranicen, ali to nam ne garantira da ne postoji neka druga okolina u kojoj infinum nije ogranicen epsilonom, sto se zahtjeva u definiciji oscilacije.
U cemu je fora?
Pozdrav.
Kaze lema 7.1:
| Kod: | | Funkcija f: A->R je neprekidna u c € A akko je O(f,c)=0. |
Dokaz kaze ovako (smjer  ): ):
Pretpostavimo da je f neprekidna u c. Tada za svaki 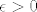 postoji postoji 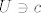 t.d. za t.d. za 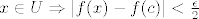
Za 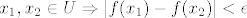 . .
Sllijedi da je 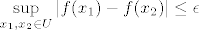
Slijedi 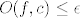 . .
 je proizvoljan je proizvoljan 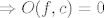
QED
Meni nikako nije jasno kako smo oscilaciju uveli u igru, tj. kako iz 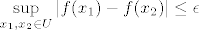 slijedi slijedi 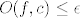 . .
Oscilacija je definirana kao 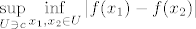 . .
To ja shvacam tako da u vanjskoj petlji (supremum) trazimo okolinu s najvecim minimumom; tj. okolinu u kojoj je 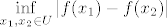 najveci, dakle okolinu u kojoj je minimum od najveci, dakle okolinu u kojoj je minimum od  najveci. najveci.
U dokazu imamo da za svaki  postoji okolina postoji okolina 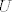 t.d. je t.d. je 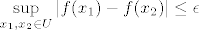 , pa onda valjda posebno i , pa onda valjda posebno i 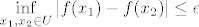 . Dakle za svaki . Dakle za svaki  postoji okolina u kojoj je infinum ogranicen, ali to nam ne garantira da ne postoji neka druga okolina u kojoj infinum nije ogranicen epsilonom, sto se zahtjeva u definiciji oscilacije. postoji okolina u kojoj je infinum ogranicen, ali to nam ne garantira da ne postoji neka druga okolina u kojoj infinum nije ogranicen epsilonom, sto se zahtjeva u definiciji oscilacije.
U cemu je fora?
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
Geliriell
Forumaš(ica)


Pridružen/a: 05. 10. 2005. (14:48:40)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
 Postano: 16:23 uto, 11. 9. 2007 Naslov: Postano: 16:23 uto, 11. 9. 2007 Naslov: |
    |
|
|
:djed: Neka je f neprekidno u c iz A i š > 0. Tada postoji U otvorena okolina od c t.d. f(A presjek U) podskup od K(f(c), š / 2), pa za proizvoljne p, q iz f(A presjek U) vrijedi d(f(p), f(q)) <= d(f(p), f(c)) + d(f(c), f(q)) < š/2 + š/2 = š.
Slijedi 0 <= o(f, c) <= diam(f(A presjek U)) <= š (prve dvije nejednakosti su očite, a zadnja slijedi iz definicije supremuma i činjenice da je š gornja međa skupa {d(f(p), f(q)) | p, q iz A presjek U}). Zaključak: o(f, c) = 0.
Obrnuto, neka je o(f, c) = 0 i š > 0. Tada iz definicije infimuma slijedi da postoji U otvorena okolina od c za koju je diam(f(A presjek U)) < š. Posebno vrijedi f(A presjek U) podskup od K(f(c), š), pa je f neprekidna u c. :faca:
 Neka je f neprekidno u c iz A i š > 0. Tada postoji U otvorena okolina od c t.d. f(A presjek U) podskup od K(f(c), š / 2), pa za proizvoljne p, q iz f(A presjek U) vrijedi d(f(p), f(q)) <= d(f(p), f(c)) + d(f(c), f(q)) < š/2 + š/2 = š. Neka je f neprekidno u c iz A i š > 0. Tada postoji U otvorena okolina od c t.d. f(A presjek U) podskup od K(f(c), š / 2), pa za proizvoljne p, q iz f(A presjek U) vrijedi d(f(p), f(q)) <= d(f(p), f(c)) + d(f(c), f(q)) < š/2 + š/2 = š.
Slijedi 0 <= o(f, c) <= diam(f(A presjek U)) <= š (prve dvije nejednakosti su očite, a zadnja slijedi iz definicije supremuma i činjenice da je š gornja međa skupa {d(f(p), f(q)) | p, q iz A presjek U}). Zaključak: o(f, c) = 0.
Obrnuto, neka je o(f, c) = 0 i š > 0. Tada iz definicije infimuma slijedi da postoji U otvorena okolina od c za koju je diam(f(A presjek U)) < š. Posebno vrijedi f(A presjek U) podskup od K(f(c), š), pa je f neprekidna u c. 
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
|





