| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 9:46 uto, 16. 10. 2007 Naslov: Zadaci sa vjezbi Postano: 9:46 uto, 16. 10. 2007 Naslov: Zadaci sa vjezbi |
    |
|
|
Imala bih par pitanja u vezi zadataka sa vjezbi.
1. Onaj primjer gdje pokazujemo da sve norme ne moraju biti ekvivalentne.
Uzmemo C([-1,1]) = {f:[-1,1]->R | f neprekidna}
I sad meni nije jasno kako mi dobijemo onu slicicu, tj. one -1/n i 1/n, odnosno n. Kasnije mi je jasno kako dobijemo funkciju, kao jednazbu pravca kroz 2 tocke, ali odakle ove tocke, zasto bas one? :?
2. Zadatak za dz, s pocetka proslih vjezbi. Treba pokazati da ako norma zadovoljava jednakost paralelograma onda postoji skalarni produkt koji ju inducira. E sad, u uputi pise da uzmemo da je (x|y)=1/4 * (||x+y||^2 - ||x-y||^2) i onda pokazemo da vrijede svojstva sklarnog produkta. Meni nije jasno zasto uzimamo da je (x|y) bas takav. Iz jednakosti paralelograma ja to bas i ne dobivam pa mi nije jasno.
Ako moza mala pomoc bila bih zahvalna. :thankyou:
Imala bih par pitanja u vezi zadataka sa vjezbi.
1. Onaj primjer gdje pokazujemo da sve norme ne moraju biti ekvivalentne.
Uzmemo C([-1,1]) = {f:[-1,1]→R | f neprekidna}
I sad meni nije jasno kako mi dobijemo onu slicicu, tj. one -1/n i 1/n, odnosno n. Kasnije mi je jasno kako dobijemo funkciju, kao jednazbu pravca kroz 2 tocke, ali odakle ove tocke, zasto bas one? 
2. Zadatak za dz, s pocetka proslih vjezbi. Treba pokazati da ako norma zadovoljava jednakost paralelograma onda postoji skalarni produkt koji ju inducira. E sad, u uputi pise da uzmemo da je (x|y)=1/4 * (||x+y||^2 - ||x-y||^2) i onda pokazemo da vrijede svojstva sklarnog produkta. Meni nije jasno zasto uzimamo da je (x|y) bas takav. Iz jednakosti paralelograma ja to bas i ne dobivam pa mi nije jasno.
Ako moza mala pomoc bila bih zahvalna. 
|
|
| [Vrh] |
|
Kobra
Forumaš(ica)

Pridružen/a: 03. 02. 2005. (10:23:52)
Postovi: (48)16
Spol: 
Lokacija: Ferenščica/Podstrana
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 10:23 uto, 16. 10. 2007 Naslov: Postano: 10:23 uto, 16. 10. 2007 Naslov: |
    |
|
|
Ovaj kolegij je nastavak analize, pa ima dosta toga di se pitaš 'Pa otkud sad to?' ( sjeti se dokaza neprekidnosti pa oni bijesni delte, pa namještanja u dokazima kod taylorovih redova...)tak da se nemoj čuditi takvom odabiru skar produkta...uzmi ga takvog kakvog je, provjeri da li taj skal produkt zadovoljava sva svojstva i da li norma inducirana tim skar produktom zadovoljava jednakost paralelograma. I gotov zadatak.
A ne znam točno kaj pitaš pod 1. Daj please napiši cijeli zadatak...mislim da je to ono kad se pokaže da besk norma ovisi o n, a neka druga ne il tak nešt slično...
edit: jel to onaj skup fja čija je vrijednost nula za x eve do -1/n i nakon 1/n a za one između se penje do n? Ak je onda se pokazuje na skupu tih fja da je jedna od normi, mislim nešt tipa max{fn(x),x iz R} ovisi o n, a neka druga da je konstantna (mislim 1)...pa onda ne postoje one konstante da bi vrijedila ona nejednakost.... ovo pišem iz sjećanja tak da moguće da ima greški...
Ovaj kolegij je nastavak analize, pa ima dosta toga di se pitaš 'Pa otkud sad to?' ( sjeti se dokaza neprekidnosti pa oni bijesni delte, pa namještanja u dokazima kod taylorovih redova...)tak da se nemoj čuditi takvom odabiru skar produkta...uzmi ga takvog kakvog je, provjeri da li taj skal produkt zadovoljava sva svojstva i da li norma inducirana tim skar produktom zadovoljava jednakost paralelograma. I gotov zadatak.
A ne znam točno kaj pitaš pod 1. Daj please napiši cijeli zadatak...mislim da je to ono kad se pokaže da besk norma ovisi o n, a neka druga ne il tak nešt slično...
edit: jel to onaj skup fja čija je vrijednost nula za x eve do -1/n i nakon 1/n a za one između se penje do n? Ak je onda se pokazuje na skupu tih fja da je jedna od normi, mislim nešt tipa max{fn(x),x iz R} ovisi o n, a neka druga da je konstantna (mislim 1)...pa onda ne postoje one konstante da bi vrijedila ona nejednakost.... ovo pišem iz sjećanja tak da moguće da ima greški...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 10:51 uto, 16. 10. 2007 Naslov: Postano: 10:51 uto, 16. 10. 2007 Naslov: |
    |
|
|
[quote="Luuka"]
A ne znam točno kaj pitaš pod 1. Daj please napiši cijeli zadatak...mislim da je to ono kad se pokaže da besk norma ovisi o n, a neka druga ne il tak nešt slično...[/quote]
Pocetak je ono sto pise gore.
I onda imamo:
||f||besk=sup |f([-1,1])|
||f||1=integral od -1 do 1 (|f(t)|dt)
tvrdimo da ne vrijedi ||.||1 ~ ||.||besk
pretpostavimo suprotno, uzmemo da postoje m, M>0 t.d.
m||f||1<=||f||besk<=M||f||1.
I onda dolazi ta slavna slika o kojoj pricam i te tocke koji mi nisu jasne odakle su ispale.
Preko tocaka dobijemo kako tocno funkcija izgleda, uzmemo da je ||f||1=1 i ||f||=n i imamo
m<=n<=M.
Pretpostavljam da sada znas o kojem primjeru pricam jer ako i nismo u istoj grupi mislim da asistenti idu po istim vjezbama.
Ako i dalje ne znas o cemu pricam probat cu malo detaljnije...
Tnx :)
| Luuka (napisa): |
A ne znam točno kaj pitaš pod 1. Daj please napiši cijeli zadatak...mislim da je to ono kad se pokaže da besk norma ovisi o n, a neka druga ne il tak nešt slično... |
Pocetak je ono sto pise gore.
I onda imamo:
||f||besk=sup |f([-1,1])|
||f||1=integral od -1 do 1 (|f(t)|dt)
tvrdimo da ne vrijedi ||.||1 ~ ||.||besk
pretpostavimo suprotno, uzmemo da postoje m, M>0 t.d.
m||f||1⇐||f||besk⇐M||f||1.
I onda dolazi ta slavna slika o kojoj pricam i te tocke koji mi nisu jasne odakle su ispale.
Preko tocaka dobijemo kako tocno funkcija izgleda, uzmemo da je ||f||1=1 i ||f||=n i imamo
m⇐n⇐M.
Pretpostavljam da sada znas o kojem primjeru pricam jer ako i nismo u istoj grupi mislim da asistenti idu po istim vjezbama.
Ako i dalje ne znas o cemu pricam probat cu malo detaljnije...
Tnx 
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:17 uto, 16. 10. 2007 Naslov: Postano: 20:17 uto, 16. 10. 2007 Naslov: |
    |
|
|
Onda se dobro sjećam... ugl pokazano je da je norma beskonačno, kod tako zadanog niza fja ovisi o n-u, a norma 1 (ona sa integralom) je za svaki n konstantna (tj 1)...integral je površina ispod grafa, a to je trokut sa stranicom 2/n i visinom n pa mu je površina 1, n se skrati.
Pošto jedna norma ovisi o n-u, tj kad n ide u beskonačno, i norma ide u beskonačno, a norma 1 je uvijek jedan pa ne postoji M,m>0 t.d
m norma besk <=norma 1<=M norm besk.
A zašto baš te fje...eh to je onaj slavni kontraprimjer...nešto izmišljeno da bi se pokazalo da nešt ne vrijedi.
Onda se dobro sjećam... ugl pokazano je da je norma beskonačno, kod tako zadanog niza fja ovisi o n-u, a norma 1 (ona sa integralom) je za svaki n konstantna (tj 1)...integral je površina ispod grafa, a to je trokut sa stranicom 2/n i visinom n pa mu je površina 1, n se skrati.
Pošto jedna norma ovisi o n-u, tj kad n ide u beskonačno, i norma ide u beskonačno, a norma 1 je uvijek jedan pa ne postoji M,m>0 t.d
m norma besk <=norma 1<=M norm besk.
A zašto baš te fje...eh to je onaj slavni kontraprimjer...nešto izmišljeno da bi se pokazalo da nešt ne vrijedi.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 10:43 uto, 23. 10. 2007 Naslov: Postano: 10:43 uto, 23. 10. 2007 Naslov: |
    |
|
|
Zadnji zadatak sa proslih vjezbi, pod b...
Treba odrediti skup gomilista skupa [latex]S_2=\lbrace (p,q) \in {\bf R}^2, p,q \in {\bf Q}\rbrace[/latex]
Meni nije jasno zasto uzimamo tocku bas iz tog trokuta, a ne bilo koju iz kugle i dokazujemo da je udaljenost manja od [latex]\epsilon[/latex]
Jel netko mozda rijesio onaj drugi dio zadatka koji nam je ostavljen za zadacu, kada je [latex]P_0\in ({\bf R}\backslash{\bf Q})\times{\bf Q}[/latex] i [latex]P_0\in {\bf Q}\times({\bf R}\backslash{\bf Q})[/latex]
Hvala
:yesss: Skuzila sam latex. :)
Zadnji zadatak sa proslih vjezbi, pod b...
Treba odrediti skup gomilista skupa 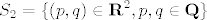
Meni nije jasno zasto uzimamo tocku bas iz tog trokuta, a ne bilo koju iz kugle i dokazujemo da je udaljenost manja od 
Jel netko mozda rijesio onaj drugi dio zadatka koji nam je ostavljen za zadacu, kada je 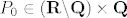 i i 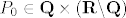
Hvala
 Skuzila sam latex. Skuzila sam latex. 
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 14:52 sub, 17. 11. 2007 Naslov: Postano: 14:52 sub, 17. 11. 2007 Naslov: |
    |
|
|
Racunam sada ove zadatke sa limesima sa zadnjih vjezbi, pa mi nesto ne stima...
Zadatak ide ovako:
[latex]f(x,y)=xy\cdot\frac{x-y}{x+y}[/latex]
Sad, prvo racunamo limes u tocki [latex](x_0,-x_0)[/latex]
Konstruiramo one nizove
[latex]x_n=x_0+\frac{1}{n}[/latex]
[latex]y_n=-x_0+\frac{1}{n}[/latex]
Uvrstimo [latex]x_n[/latex] i [latex]y_n[/latex] u funkciju i dobijemo da je [latex]f(x_n,y_n)=nx_0[/latex]
Racunamo limes i odbivamo
[latex]\lim_{n \to \infty} f(x_n,y_n)=\left\{ \begin{array}{ll}
+\infty, & \mbox {$x_0>0$} \\
-\infty, & \mbox {$x_0<0$}\end{array} \right[/latex]
Taj dio mi je jasan.
Sad racunamo kada je [latex](x_0,-x_0)=(0,0)[/latex]
Onaj prvi dio kada dobijemo da je limes nula razumijem.
Kuzim i sta smo radili sa onim sin i cos, ali me muci onaj zadnji red...
Naime, nakon svog onog racunanja dobili smo
[latex]f(x_n,y_n)=\frac {-1}{2n^2}\cdot \cos\frac{2}{n^2}\cdot \frac{\cos\frac{1}{n^2}}{\sin\frac{1}{n^2}}[/latex]
Rastavimo do na 2 limesa i sad meni pise ovako:
onaj prvi dio nije bitan, muci me ovo
[latex]\lim_{n \to \infty}\frac{\frac{1}{n^2}}{\sin\frac{1}{n^2}}=1[/latex]
Koliko mene znanje analize sluzi, to vrijedi kada [latex]n \to 0[/latex]
Cak sam i u staru biljeznicu isla gledati, pise da je taj limes jednak 0 kada n ide u beskonacnost, a 1 kada n ide u 0...
E sad, ne znam jesam li je mozad krivo zapisala, pa s obzirom da trazimo limes u (0,0) stavljamo [latex]n \to 0[/latex]... :?
uglavnom, valjda ste skuzili pitanje. :)
Racunam sada ove zadatke sa limesima sa zadnjih vjezbi, pa mi nesto ne stima...
Zadatak ide ovako:
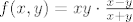
Sad, prvo racunamo limes u tocki 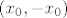
Konstruiramo one nizove
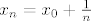
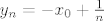
Uvrstimo 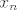 i i 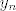 u funkciju i dobijemo da je u funkciju i dobijemo da je 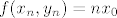
Racunamo limes i odbivamo
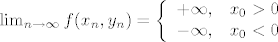
Taj dio mi je jasan.
Sad racunamo kada je 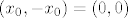
Onaj prvi dio kada dobijemo da je limes nula razumijem.
Kuzim i sta smo radili sa onim sin i cos, ali me muci onaj zadnji red...
Naime, nakon svog onog racunanja dobili smo
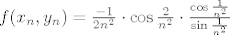
Rastavimo do na 2 limesa i sad meni pise ovako:
onaj prvi dio nije bitan, muci me ovo
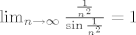
Koliko mene znanje analize sluzi, to vrijedi kada 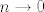
Cak sam i u staru biljeznicu isla gledati, pise da je taj limes jednak 0 kada n ide u beskonacnost, a 1 kada n ide u 0...
E sad, ne znam jesam li je mozad krivo zapisala, pa s obzirom da trazimo limes u (0,0) stavljamo 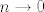 ... ... 
uglavnom, valjda ste skuzili pitanje. 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:58 sub, 17. 11. 2007 Naslov: Postano: 14:58 sub, 17. 11. 2007 Naslov: |
    |
|
|
Argument ti je 1/n^2. A kad n ide u besk onda 1/n^2 ide u nulu, a to je ono kaj se traži...
Argument ti je 1/n^2. A kad n ide u besk onda 1/n^2 ide u nulu, a to je ono kaj se traži...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
jerry
Forumaš(ica)
Pridružen/a: 19. 11. 2007. (01:47:33)
Postovi: (B)16
|
|
| [Vrh] |
|
Blatko
Forumaš(ica)

Pridružen/a: 12. 07. 2007. (11:25:44)
Postovi: (5D)16
|
|
| [Vrh] |
|
jerry
Forumaš(ica)
Pridružen/a: 19. 11. 2007. (01:47:33)
Postovi: (B)16
|
|
| [Vrh] |
|
|




















