| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
buzov5
Forumaš(ica)

Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
the maja
Forumaš(ica)

Pridružen/a: 26. 11. 2006. (09:35:27)
Postovi: (5D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:31 sub, 2. 2. 2008 Naslov: Postano: 17:31 sub, 2. 2. 2008 Naslov: |
    |
|
|
prirast==derivacija (općenito)
Najveći prirast==najveća derivacija u smjeru nekog vektora (na Rn)
I sad da dobiješ najveći prrirast tražiš vektor t.d. je derivacija u njegovom smjeru najveća.
prirast==derivacija (općenito)
Najveći prirast==najveća derivacija u smjeru nekog vektora (na Rn)
I sad da dobiješ najveći prrirast tražiš vektor t.d. je derivacija u njegovom smjeru najveća.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
buzov5
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 10:56 ned, 3. 2. 2008 Naslov: Postano: 10:56 ned, 3. 2. 2008 Naslov: |
    |
|
|
[url]http://web.math.hr/nastava/difraf/dif/vj6.pdf[/url]
Vidi zadatak 6.2. (btw greška je, fja ide u R a ne Rm)
Dakle tražiš po kojem vektoru (iz neke točke) se moraš kretati da bi 'derivacija' (tj brzina) bila najveća.
U konkretnom zadatku (6.2) ona nejednakost je SCB.
A ne znam dal fje kojima se gleda najveći prirast moraju ić u R ili mogu i u Rn. Nek se tu izjasni ko je siguran.
http://web.math.hr/nastava/difraf/dif/vj6.pdf
Vidi zadatak 6.2. (btw greška je, fja ide u R a ne Rm)
Dakle tražiš po kojem vektoru (iz neke točke) se moraš kretati da bi 'derivacija' (tj brzina) bila najveća.
U konkretnom zadatku (6.2) ona nejednakost je SCB.
A ne znam dal fje kojima se gleda najveći prirast moraju ić u R ili mogu i u Rn. Nek se tu izjasni ko je siguran.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
buzov5
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:01 ned, 3. 2. 2008 Naslov: Postano: 17:01 ned, 3. 2. 2008 Naslov: |
    |
|
|
Tu ima posla. Najprije se nađe diferencijal (što je 3 x 2 matrica). Onda nađeš točku (x,y) koja se preslikala u danu točnu na plohi, takle sustav 3 jedn sa 2 nepoznanice. Onda tu točku ubaciš u diferencijal, uzmeš stupce svaki posebno, tretiraš ih kao vektore i ubaciš u determinantu koja u prvom retku ima i j k a u druga 2 retka ta 2 stupca. I sad ta determinanta treba bit 0. I tu dobiješ vektor normale tangencijalne ravnine. Sad imaš vektor normale, i točku pa znaš i jedn ravnine.
:)
Tu ima posla. Najprije se nađe diferencijal (što je 3 x 2 matrica). Onda nađeš točku (x,y) koja se preslikala u danu točnu na plohi, takle sustav 3 jedn sa 2 nepoznanice. Onda tu točku ubaciš u diferencijal, uzmeš stupce svaki posebno, tretiraš ih kao vektore i ubaciš u determinantu koja u prvom retku ima i j k a u druga 2 retka ta 2 stupca. I sad ta determinanta treba bit 0. I tu dobiješ vektor normale tangencijalne ravnine. Sad imaš vektor normale, i točku pa znaš i jedn ravnine.

_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 17:42 ned, 3. 2. 2008 Naslov: Postano: 17:42 ned, 3. 2. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Tu ima posla. Najprije se nađe diferencijal (što je 3 x 2 matrica). Onda nađeš točku (x,y) koja se preslikala u danu točnu na plohi, takle sustav 3 jedn sa 2 nepoznanice. Onda tu točku ubaciš u diferencijal, uzmeš stupce svaki posebno, tretiraš ih kao vektore i ubaciš u determinantu koja u prvom retku ima i j k a u druga 2 retka ta 2 stupca. I sad ta determinanta treba bit 0. I tu dobiješ vektor normale tangencijalne ravnine. Sad imaš vektor normale, i točku pa znaš i jedn ravnine.
:)[/quote]
Ja dobijem 2 točke, (1,2) i (2,1)....
I mogu ja sad recimo ici ovim postupkom sta si obasnio, ali meni uopce nije jasno zasto to tako ide.... Jel to ista shema kao u [url=http://web.math.hr/nastava/difraf/dif/vj6.pdf]zadatku 6.4[/url], samo sta prvo moram naci tocku? :?
Ispricavam se sta pitam gluposti, ali jednostavno mi ove plohe ne idu... Sve drugo kuzim, ali ovo me izludjuje, uopce si ne mogu to sve skupa predociti tak da jedva hvatam sta treba raditi. :oops:
Hvala :)
| Luuka (napisa): | Tu ima posla. Najprije se nađe diferencijal (što je 3 x 2 matrica). Onda nađeš točku (x,y) koja se preslikala u danu točnu na plohi, takle sustav 3 jedn sa 2 nepoznanice. Onda tu točku ubaciš u diferencijal, uzmeš stupce svaki posebno, tretiraš ih kao vektore i ubaciš u determinantu koja u prvom retku ima i j k a u druga 2 retka ta 2 stupca. I sad ta determinanta treba bit 0. I tu dobiješ vektor normale tangencijalne ravnine. Sad imaš vektor normale, i točku pa znaš i jedn ravnine.
 |
Ja dobijem 2 točke, (1,2) i (2,1)....
I mogu ja sad recimo ici ovim postupkom sta si obasnio, ali meni uopce nije jasno zasto to tako ide.... Jel to ista shema kao u zadatku 6.4, samo sta prvo moram naci tocku? 
Ispricavam se sta pitam gluposti, ali jednostavno mi ove plohe ne idu... Sve drugo kuzim, ali ovo me izludjuje, uopce si ne mogu to sve skupa predociti tak da jedva hvatam sta treba raditi. 
Hvala 
_________________  |
|
| [Vrh] |
|
noa
Forumaš(ica)
Pridružen/a: 14. 04. 2007. (22:28:08)
Postovi: (51)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:50 ned, 3. 2. 2008 Naslov: Postano: 17:50 ned, 3. 2. 2008 Naslov: |
    |
|
|
[quote="desire"]
Ja dobijem 2 točke, (1,2) i (2,1)....
[/quote]
Svejedno koju ubaciš, na kraju vektor normale ispadne isti (ili kolinearan)
I da, to je ko u 6.4.
| desire (napisa): |
Ja dobijem 2 točke, (1,2) i (2,1)....
|
Svejedno koju ubaciš, na kraju vektor normale ispadne isti (ili kolinearan)
I da, to je ko u 6.4.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 17:52 ned, 3. 2. 2008 Naslov: Postano: 17:52 ned, 3. 2. 2008 Naslov: |
    |
|
|
[quote="Luuka"][quote="desire"]
Ja dobijem 2 točke, (1,2) i (2,1)....
[/quote]
Svejedno koju ubaciš, na kraju vektor normale ispadne isti (ili kolinearan)
I da, to je ko u 6.4.[/quote]
Hvala. :)
| Luuka (napisa): | | desire (napisa): |
Ja dobijem 2 točke, (1,2) i (2,1)....
|
Svejedno koju ubaciš, na kraju vektor normale ispadne isti (ili kolinearan)
I da, to je ko u 6.4. |
Hvala. 
_________________  |
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 18:06 ned, 3. 2. 2008 Naslov: Postano: 18:06 ned, 3. 2. 2008 Naslov: |
    |
|
|
Zadaca - diferencijabilnost, zadatak5, dobivate li veliku vrijednost za diferencijal u tocki (1,2,3,2) od vektora (1,1,1,1) :?:
ps: kad kazem veliku mislim na skoro pola milijarde. :o
Zadaca - diferencijabilnost, zadatak5, dobivate li veliku vrijednost za diferencijal u tocki (1,2,3,2) od vektora (1,1,1,1) 
ps: kad kazem veliku mislim na skoro pola milijarde. 
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 19:10 ned, 3. 2. 2008 Naslov: Postano: 19:10 ned, 3. 2. 2008 Naslov: |
    |
|
|
[quote="RonnieColeman"]Zadaca - diferencijabilnost, zadatak5, dobivate li veliku vrijednost za diferencijal u tocki (1,2,3,2) od vektora (1,1,1,1) :?:
ps: kad kazem veliku mislim na skoro pola milijarde. :o[/quote]
Kako si ti to rjesavao? Ja sam to rjesavala slicno [url=http://web.math.hr/nastava/difraf/dif/vj5.pdf]zadatku 5.11[/url].
Za f1 sam uzela (x1^2*x3, x2*x4^2).
f2=||x||^2
f3=x^5
f=(f3◦f2◦f1)(x)
Al me muci to sta mi je Df1(x) matrica s kojom onda ne znam sta bi kad to sve izderiviram. :?
| RonnieColeman (napisa): | Zadaca - diferencijabilnost, zadatak5, dobivate li veliku vrijednost za diferencijal u tocki (1,2,3,2) od vektora (1,1,1,1) 
ps: kad kazem veliku mislim na skoro pola milijarde.  |
Kako si ti to rjesavao? Ja sam to rjesavala slicno zadatku 5.11.
Za f1 sam uzela (x1^2*x3, x2*x4^2).
f2=||x||^2
f3=x^5
f=(f3◦f2◦f1)(x)
Al me muci to sta mi je Df1(x) matrica s kojom onda ne znam sta bi kad to sve izderiviram. 
_________________  |
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 19:40 ned, 3. 2. 2008 Naslov: Postano: 19:40 ned, 3. 2. 2008 Naslov: |
    |
|
|
Ovako:
Neka je c@IR^4 , c=(c1,c2,c3,c4).
Neka je h : IR^4 -> IR^2, h(x1,x2,x3,x4)=(x1^2 * x3, x2 * x4^2)
Neka je Im(h) = A
Neka je g : A -> IR, g(x1^2 * x3, x2*x4^2) = ||(x1^2 * x3, x2 * x4^2|| = [(x1^2 * x3)^2 + (x2 * x4^2)^2 ]^5
-h je dfb jer su njene komponentne funkcije dfbe
(koordinatna projekcija je dfb funkcija, produkt dfb funkcija je dfb funkcija)
-norma(Euklidska) je dfb => g je dfb.
-kompozicija dfb funkcija je dfb funkcija => goh=f je dfb.
Dakle, ima smisla "natjeravati" diferencijal funkcije f.
Df(c)=Dgoh(c)=Dg(h(c))oDh(c)
u točkama:
Df(c)(x1,x2,x3,x4)=Dgoh(c)(x1,x2,x3,x4)=Dg(h(c))oDh(c)(x1,x2,x3,x4)
Identifikacija sa Jacobijevim matricama:
Napomena(Nabla je onaj obrnuti trokut koji označava Jac.matricu)
Nabla g(h(c)) * (Nabla h(c) * (x1,x2,x3,x4) ), gdje je (x1,x2,x3,x4) vektor stupac
Nabla h(c) =
prvi redak: 2c1c3 0 c1^2 0
drugi redak: 0 c4^2 0 2c2c4
Nabla h(c) * (x1,x2,x3,x4) =
prvi redak: 2c1c3x1 + c1^2 * x3
drugi redak: c4^2 * x2 + 2c2c4x4
h(c)=(c1^2 * c3, c2 * c4^2), y=(y1,y2)@IR^2
Nabla (h(c)) =
prvi redak: 10[(c1^2 * c3)^2]^4 * (c1^2 * c3)
drugi redak: 10[(c1^2 * c3)^2]^4 * (c2c4^2)
To je to, sada se pomnože dobivene matrice i to je djelovanje diferencijala funkcije f u točki c od proizvoljnog vektora (x1,x2,x3,x4).
E sad, drugi je par rukavica činjenica da mi je diferencijal u konkretno zadanoj točki od konkretno zadanog vektora golem! (oko 3 milijarde u zadnjem računanju)
Ovako:
Neka je c@IR^4 , c=(c1,c2,c3,c4).
Neka je h : IR^4 → IR^2, h(x1,x2,x3,x4)=(x1^2 * x3, x2 * x4^2)
Neka je Im(h) = A
Neka je g : A → IR, g(x1^2 * x3, x2*x4^2) = ||(x1^2 * x3, x2 * x4^2|| = [(x1^2 * x3)^2 + (x2 * x4^2)^2 ]^5
-h je dfb jer su njene komponentne funkcije dfbe
(koordinatna projekcija je dfb funkcija, produkt dfb funkcija je dfb funkcija)
-norma(Euklidska) je dfb ⇒ g je dfb.
-kompozicija dfb funkcija je dfb funkcija ⇒ goh=f je dfb.
Dakle, ima smisla "natjeravati" diferencijal funkcije f.
Df(c)=Dgoh(c)=Dg(h(c))oDh(c)
u točkama:
Df(c)(x1,x2,x3,x4)=Dgoh(c)(x1,x2,x3,x4)=Dg(h(c))oDh(c)(x1,x2,x3,x4)
Identifikacija sa Jacobijevim matricama:
Napomena(Nabla je onaj obrnuti trokut koji označava Jac.matricu)
Nabla g(h(c)) * (Nabla h(c) * (x1,x2,x3,x4) ), gdje je (x1,x2,x3,x4) vektor stupac
Nabla h(c) =
prvi redak: 2c1c3 0 c1^2 0
drugi redak: 0 c4^2 0 2c2c4
Nabla h(c) * (x1,x2,x3,x4) =
prvi redak: 2c1c3x1 + c1^2 * x3
drugi redak: c4^2 * x2 + 2c2c4x4
h(c)=(c1^2 * c3, c2 * c4^2), y=(y1,y2)@IR^2
Nabla (h(c)) =
prvi redak: 10[(c1^2 * c3)^2]^4 * (c1^2 * c3)
drugi redak: 10[(c1^2 * c3)^2]^4 * (c2c4^2)
To je to, sada se pomnože dobivene matrice i to je djelovanje diferencijala funkcije f u točki c od proizvoljnog vektora (x1,x2,x3,x4).
E sad, drugi je par rukavica činjenica da mi je diferencijal u konkretno zadanoj točki od konkretno zadanog vektora golem! (oko 3 milijarde u zadnjem računanju)
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 20:03 ned, 3. 2. 2008 Naslov: Postano: 20:03 ned, 3. 2. 2008 Naslov: |
    |
|
|
[quote="RonnieColeman"]
Neka je g : A -> IR, g(x1^2 * x3, x2*x4^2) = ||(x1^2 * x3, x2 * x4^2|| = [(x1^2 * x3)^2 + (x2 * x4^2)^2 ]^5
[/quote]
Da, moze se i tako gledati, ali ti si ovdje u principu raspisao ovaj izraz, a ja sam isla na cistu kompoziciju jer nemam pojma smijemo li to tako raspisivati.
Ko sta je u onom zadatku na koji sam dala link ja sam isla na to da je diferencijal od f2=||x||^2=(x|x) i Df2(x)(H)=2(x|H) i tu sam se zaplela kasnije u raspisivanju...
Ako smijemo kako si ti napisao ok, ali ako tu normu ne smijemo rastavljati nego upotrijebiti ovo onda ne znam....
| RonnieColeman (napisa): |
Neka je g : A → IR, g(x1^2 * x3, x2*x4^2) = ||(x1^2 * x3, x2 * x4^2|| = [(x1^2 * x3)^2 + (x2 * x4^2)^2 ]^5
|
Da, moze se i tako gledati, ali ti si ovdje u principu raspisao ovaj izraz, a ja sam isla na cistu kompoziciju jer nemam pojma smijemo li to tako raspisivati.
Ko sta je u onom zadatku na koji sam dala link ja sam isla na to da je diferencijal od f2=||x||^2=(x|x) i Df2(x)(H)=2(x|H) i tu sam se zaplela kasnije u raspisivanju...
Ako smijemo kako si ti napisao ok, ali ako tu normu ne smijemo rastavljati nego upotrijebiti ovo onda ne znam....
_________________  |
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 20:26 ned, 3. 2. 2008 Naslov: Postano: 20:26 ned, 3. 2. 2008 Naslov: |
    |
|
|
[quote="desire"][quote="RonnieColeman"]
Neka je g : A -> IR, g(x1^2 * x3, x2*x4^2) = ||(x1^2 * x3, x2 * x4^2||^10 = [(x1^2 * x3)^2 + (x2 * x4^2)^2 ]^5
[/quote]
Da, moze se i tako gledati, ali ti si ovdje u principu raspisao ovaj izraz, a ja sam isla na cistu kompoziciju jer nemam pojma smijemo li to tako raspisivati. [/quote]
Zašto ne bismo smjeli?
Ja sam raspisao normu onakvom kakva jest.
Ne može mi se zamjeriti uzimanje Euklidske norme jer su sve norme na IR^n ekvivalentne.
[quote]
Ko sta je u onom zadatku na koji sam dala link ja sam isla na to da je diferencijal od f2=||x||^2=(x|x) i Df2(x)(H)=2(x|H) i tu sam se zaplela kasnije u raspisivanju... [/quote]
Nisam išao tim putem, vjerojatno treba, nekako, iskoristiti ovo:
||x||^2 * ||x||^2 * ||x||^2 * ||x||^2 * ||x||^2 = ||x||^10
| desire (napisa): | | RonnieColeman (napisa): |
Neka je g : A → IR, g(x1^2 * x3, x2*x4^2) = ||(x1^2 * x3, x2 * x4^2||^10 = [(x1^2 * x3)^2 + (x2 * x4^2)^2 ]^5
|
Da, moze se i tako gledati, ali ti si ovdje u principu raspisao ovaj izraz, a ja sam isla na cistu kompoziciju jer nemam pojma smijemo li to tako raspisivati. |
Zašto ne bismo smjeli?
Ja sam raspisao normu onakvom kakva jest.
Ne može mi se zamjeriti uzimanje Euklidske norme jer su sve norme na IR^n ekvivalentne.
| Citat: |
Ko sta je u onom zadatku na koji sam dala link ja sam isla na to da je diferencijal od f2=||x||^2=(x|x) i Df2(x)(H)=2(x|H) i tu sam se zaplela kasnije u raspisivanju... |
Nisam išao tim putem, vjerojatno treba, nekako, iskoristiti ovo:
||x||^2 * ||x||^2 * ||x||^2 * ||x||^2 * ||x||^2 = ||x||^10
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 20:45 ned, 3. 2. 2008 Naslov: Postano: 20:45 ned, 3. 2. 2008 Naslov: |
    |
|
|
Ja sam još davno na nekim vježbama pitao asistenticu Tadić za taj zadatak i rekla je da idu tri kompozicije: projekcija, norma i potencija.
Nego dali netko zna riješiti nešto od sljedećeg:
1. Pokažite da Hesseove matrice funkcije [latex] f(x,y,z)=x^2-z^2 [/latex] u stacionarnim točkama nisu semidefinitne. Nadalje karakterizirajte stacionarne točke funkcije f.
2. Pokažite da se najmanja i najveća vrijednost funkcije f postiže na rubu domene.
[latex] f:K\rightarrow \mathbb{R}, f(x,y)=x^4+y^4-2x^2+4xy\ K\subset \mathbb{R}[/latex] kompaktan.
3. Neka je [latex] f:A\subset \mathbb{R}^n \rightarrow \mathbb{R}[/latex] preslikavanje klase [latex] C^r [/latex] na otvorenom skupu A i neka je [latex] x_0\in A[/latex] točka za koju je ispunjeno sljedeće:
[latex] D_f(x_0)=0, D^2_f(x_0)=0,.....,D^{r-1}_f(x_0)=0, D^r_f(x_0)<0, \forall x\in \mathbb{R} [/latex] bez 0.
Dokažite da f ima lokalni maksimum u [latex] x_0 [/latex].
Ja sam još davno na nekim vježbama pitao asistenticu Tadić za taj zadatak i rekla je da idu tri kompozicije: projekcija, norma i potencija.
Nego dali netko zna riješiti nešto od sljedećeg:
1. Pokažite da Hesseove matrice funkcije 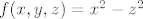 u stacionarnim točkama nisu semidefinitne. Nadalje karakterizirajte stacionarne točke funkcije f. u stacionarnim točkama nisu semidefinitne. Nadalje karakterizirajte stacionarne točke funkcije f.
2. Pokažite da se najmanja i najveća vrijednost funkcije f postiže na rubu domene.
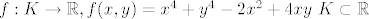 kompaktan. kompaktan.
3. Neka je 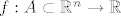 preslikavanje klase preslikavanje klase 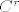 na otvorenom skupu A i neka je na otvorenom skupu A i neka je 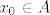 točka za koju je ispunjeno sljedeće: točka za koju je ispunjeno sljedeće:
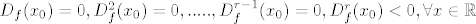 bez 0. bez 0.
Dokažite da f ima lokalni maksimum u 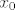 . .
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:52 ned, 3. 2. 2008 Naslov: Postano: 20:52 ned, 3. 2. 2008 Naslov: |
    |
|
|
2. reko bi da je K unutar R2. A to pokažeš ovak: ideš tražit stac točke na stand način i vj se dobije da su sedlo. Pa ti kažeš da pošto je K kompaktan, f nepr da se mora dostić minimum i maksimum. Pošto to nije postigla na IntK (nije na nijednom otv skupu, pa ni na najvećem mogućem) onda se min i max postižu na rubu od K.
2. reko bi da je K unutar R2. A to pokažeš ovak: ideš tražit stac točke na stand način i vj se dobije da su sedlo. Pa ti kažeš da pošto je K kompaktan, f nepr da se mora dostić minimum i maksimum. Pošto to nije postigla na IntK (nije na nijednom otv skupu, pa ni na najvećem mogućem) onda se min i max postižu na rubu od K.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|




















