| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Undómiel
Forumaš(ica)


Pridružen/a: 31. 01. 2008. (20:26:57)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
Undómiel
Forumaš(ica)


Pridružen/a: 31. 01. 2008. (20:26:57)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
Undómiel
Forumaš(ica)


Pridružen/a: 31. 01. 2008. (20:26:57)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
 Postano: 19:49 uto, 5. 2. 2008 Naslov: Postano: 19:49 uto, 5. 2. 2008 Naslov: |
    |
|
|
Traženi ostatak je polinom drugog stupnja, ax^2 + bx + c, pa vrijedi
(1) f(x) = x^2(x - 1)q(x) + ax^2 + bx + c; za svaki x iz R
za neki polinom q. Uvrštavanjem x = 0 dobije se c = 0, a uvrštavanjem x = 1 dobivamo a + b + c = -9. Deriviranjem jednakosti (1) dobivamo
f'(x) = (3x^2 - 2x) q(x) + x^2(x - 1) q'(x) + 2ax + b; za svaki x iz R
Vrijedi f'(x) = 600x^599 - 3600x^59 - 256x^15 + 66, pa uvrštavanjem x = 0 dobivamo treću jednakost b = 66.
Rješavanjem dobivenog sustava nalazimo a = -75, b = 66, c = 0, pa je traženi ostatak jednak -75x^2 + 66x.
Još pregledaj, ovo ti je nabrzaka... :?
Traženi ostatak je polinom drugog stupnja, ax^2 + bx + c, pa vrijedi
(1) f(x) = x^2(x - 1)q(x) + ax^2 + bx + c; za svaki x iz R
za neki polinom q. Uvrštavanjem x = 0 dobije se c = 0, a uvrštavanjem x = 1 dobivamo a + b + c = -9. Deriviranjem jednakosti (1) dobivamo
f'(x) = (3x^2 - 2x) q(x) + x^2(x - 1) q'(x) + 2ax + b; za svaki x iz R
Vrijedi f'(x) = 600x^599 - 3600x^59 - 256x^15 + 66, pa uvrštavanjem x = 0 dobivamo treću jednakost b = 66.
Rješavanjem dobivenog sustava nalazimo a = -75, b = 66, c = 0, pa je traženi ostatak jednak -75x^2 + 66x.
Još pregledaj, ovo ti je nabrzaka... 
_________________
Da li je napredak kad ljudozder uzme vilicu?
|
|
| [Vrh] |
|
Undómiel
Forumaš(ica)


Pridružen/a: 31. 01. 2008. (20:26:57)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:58 uto, 5. 2. 2008 Naslov: Postano: 19:58 uto, 5. 2. 2008 Naslov: |
    |
|
|
Evo sad i ja baš gledam jedan riješeni primjer iz skripte Pavković/Veljan.
Također se traži ostatak pri djeljenju polinoma.
[latex]f(x)=x^{100}+3x^{99}+x^2-3x+9[/latex]
[latex]g(x)=x^2+2x-3[/latex], dakle
[latex]r(x)=Ax+B[/latex]
Nađemo nultočke od [latex]g(x)[/latex], koje ispadnu [latex]x_1=1,x_2=-3[/latex]
E sad veli "Dobili smo sustav jednadžbi:"
[latex]11=A+B[/latex]
[latex]27=-3A+B[/latex]
Ok, jasni su mi izrazi sa desne strane, to je [latex]r(x)[/latex].
No što je ovo sa lijeve strane?
U prvom slučaju je to [latex]x^{100}+3x^{99}+x^2-3x+9[/latex]
A u drugom samo [latex]x^2-3x+9[/latex]
:? Zašto je to tako?
Evo sad i ja baš gledam jedan riješeni primjer iz skripte Pavković/Veljan.
Također se traži ostatak pri djeljenju polinoma.
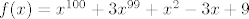
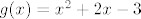 , dakle , dakle
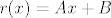
Nađemo nultočke od 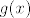 , koje ispadnu , koje ispadnu 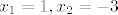
E sad veli "Dobili smo sustav jednadžbi:"
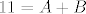
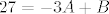
Ok, jasni su mi izrazi sa desne strane, to je 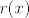 . .
No što je ovo sa lijeve strane?
U prvom slučaju je to 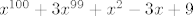
A u drugom samo 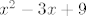
 Zašto je to tako? Zašto je to tako?
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
k8yvis
Forumaš(ica)

Pridružen/a: 13. 10. 2006. (14:32:30)
Postovi: (79)16
Spol: 
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Undómiel
Forumaš(ica)


Pridružen/a: 31. 01. 2008. (20:26:57)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
Taurus
Forumaš(ica)

Pridružen/a: 05. 02. 2008. (23:11:51)
Postovi: (61)16
Spol: 
Lokacija: Psychiatric Mental Facility (PMF)
|
 Postano: 0:04 sri, 6. 2. 2008 Naslov: Postano: 0:04 sri, 6. 2. 2008 Naslov: |
    |
|
|
Ja sam to rješio, i mislim da bi tako trebalo ići, tako da uvrstiš X = 1 i X = -1, i onda imaš (gledajući da je a(n), a(n-2), .. uz parne potencije, te a(n-1), a(n-3), .. uz neparne potencije, ja sam to tako i definirao) : (1^2 + 1 + 1)^n = a(n) + a(n-1) + ... + a(0) i ((-1)^2 - 1 + 1)^n = a(n) - a(n -1) + ... -a(1) + a(0). To dvoje zbrojis i onda imas 3^n + 1 = 2*(a(n) + a(n-2) + ... + a(2) + a(0)). Podjelis s dva i zamjeniš strane i ispadne : a(n) + a(n-2) + ... + a(2) + a(0) = (3^n + 1)/2
A sad jel to dobro il ne, no idea..
Ja sam to rješio, i mislim da bi tako trebalo ići, tako da uvrstiš X = 1 i X = -1, i onda imaš (gledajući da je a(n), a(n-2), .. uz parne potencije, te a(n-1), a(n-3), .. uz neparne potencije, ja sam to tako i definirao) : (1^2 + 1 + 1)^n = a(n) + a(n-1) + ... + a(0) i ((-1)^2 - 1 + 1)^n = a(n) - a(n -1) + ... -a(1) + a(0). To dvoje zbrojis i onda imas 3^n + 1 = 2*(a(n) + a(n-2) + ... + a(2) + a(0)). Podjelis s dva i zamjeniš strane i ispadne : a(n) + a(n-2) + ... + a(2) + a(0) = (3^n + 1)/2
A sad jel to dobro il ne, no idea..
_________________
Moooooooooooooooooooooooo...
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 0:35 sri, 6. 2. 2008 Naslov: Postano: 0:35 sri, 6. 2. 2008 Naslov: |
    |
|
|
[quote="Taurus"]Ja sam to rješio, i mislim da bi tako trebalo ići, tako da uvrstiš X = 1 i X = -1, i onda imaš (gledajući da je a(n), a(n-2), .. uz parne potencije, te a(n-1), a(n-3), .. uz neparne potencije, ja sam to tako i definirao) : (1^2 + 1 + 1)^n = a(n) + a(n-1) + ... + a(0) i ((-1)^2 - 1 + 1)^n = a(n) - a(n -1) + ... -a(1) + a(0). To dvoje zbrojis i onda imas 3^n + 1 = 2*(a(n) + a(n-2) + ... + a(2) + a(0)). Podjelis s dva i zamjeniš strane i ispadne : a(n) + a(n-2) + ... + a(2) + a(0) = (3^n + 1)/2
A sad jel to dobro il ne, no idea..[/quote]
je. to je dobro riješeno, s tim da nije a(n)+a(n-2)...+a(2)+a(0), nego a(2n)+a(2n-2)...+a(2)+a(0). :wink:
| Taurus (napisa): | Ja sam to rješio, i mislim da bi tako trebalo ići, tako da uvrstiš X = 1 i X = -1, i onda imaš (gledajući da je a(n), a(n-2), .. uz parne potencije, te a(n-1), a(n-3), .. uz neparne potencije, ja sam to tako i definirao) : (1^2 + 1 + 1)^n = a(n) + a(n-1) + ... + a(0) i ((-1)^2 - 1 + 1)^n = a(n) - a(n -1) + ... -a(1) + a(0). To dvoje zbrojis i onda imas 3^n + 1 = 2*(a(n) + a(n-2) + ... + a(2) + a(0)). Podjelis s dva i zamjeniš strane i ispadne : a(n) + a(n-2) + ... + a(2) + a(0) = (3^n + 1)/2
A sad jel to dobro il ne, no idea.. |
je. to je dobro riješeno, s tim da nije a(n)+a(n-2)...+a(2)+a(0), nego a(2n)+a(2n-2)...+a(2)+a(0). 
_________________
ima let u finish
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|




















