| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Taurus
Forumaš(ica)

Pridružen/a: 05. 02. 2008. (23:11:51)
Postovi: (61)16
Spol: 
Lokacija: Psychiatric Mental Facility (PMF)
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Taurus
Forumaš(ica)

Pridružen/a: 05. 02. 2008. (23:11:51)
Postovi: (61)16
Spol: 
Lokacija: Psychiatric Mental Facility (PMF)
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
 Postano: 21:38 sri, 13. 2. 2008 Naslov: Postano: 21:38 sri, 13. 2. 2008 Naslov: |
    |
|
|
Evo ti primjer za jednostavnu matricu tipa 4x5 :)
[color=red]2[/color] 4 2 1 -1
0 1 -3 2 0
2 5 -1 5 -1
4 9 1 4 -2
L je uvijek donje trokutasta matrica s [color=purple]1[/color] na dijagonali. Dok primjenjuješ Gaussove eliminacije, u L upisuješ skalare s kojima množiš određeni redak, ali s promjenjenim predznakom. Npr, poćet ćemo s gore označenim brojem [color=red]2[/color]. Očito ćeš drugi redak preskočiti (tj. množiš s [color=green]0[/color] i dodaješ ništa). Za treći redak: množiš prvi red s -1 i dodaješ trećem -> promjena predznaka: [color=brown]1[/color], stavljaš na pripadajuće mjesto u L matricu. Za četvrti redak: množiš prvi red s -2 i dodaješ zadnjem -> promjena predznaka: [color=blue]2[/color], stavljaš na pripadajuće mjesto u L matricu.
Sve to zvuči čudno i ne dovoljno objašnjeno, no zato sam koristio boje :D Dakle, kad provedeš sve moguće Gaussove eliminacije i dobiješ matricu U, matrica L će ovako izgledati:
[color=purple]1[/color] 0 0 0
[color=green]0[/color] [color=purple]1[/color] 0 0
[color=brown]1[/color] 1 [color=purple]1[/color] 0
[color=blue]2[/color] 1 0 [color=purple]1[/color]
A matrica U će biti slijedeća:
2 4 2 1 -1
0 1 -3 2 0
0 0 0 2 0
0 0 0 0 0
r(A) = r(U) = 3
Probaj to rješiti na papiru, trebao bi shvatiti. :)
Evo ti primjer za jednostavnu matricu tipa 4x5 
2 4 2 1 -1
0 1 -3 2 0
2 5 -1 5 -1
4 9 1 4 -2
L je uvijek donje trokutasta matrica s 1 na dijagonali. Dok primjenjuješ Gaussove eliminacije, u L upisuješ skalare s kojima množiš određeni redak, ali s promjenjenim predznakom. Npr, poćet ćemo s gore označenim brojem 2. Očito ćeš drugi redak preskočiti (tj. množiš s 0 i dodaješ ništa). Za treći redak: množiš prvi red s -1 i dodaješ trećem → promjena predznaka: 1, stavljaš na pripadajuće mjesto u L matricu. Za četvrti redak: množiš prvi red s -2 i dodaješ zadnjem → promjena predznaka: 2, stavljaš na pripadajuće mjesto u L matricu.
Sve to zvuči čudno i ne dovoljno objašnjeno, no zato sam koristio boje  Dakle, kad provedeš sve moguće Gaussove eliminacije i dobiješ matricu U, matrica L će ovako izgledati: Dakle, kad provedeš sve moguće Gaussove eliminacije i dobiješ matricu U, matrica L će ovako izgledati:
1 0 0 0
0 1 0 0
1 1 1 0
2 1 0 1
A matrica U će biti slijedeća:
2 4 2 1 -1
0 1 -3 2 0
0 0 0 2 0
0 0 0 0 0
r(A) = r(U) = 3
Probaj to rješiti na papiru, trebao bi shvatiti. 
_________________
Cry havoc, and let loose the dogs of war!
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 22:26 sri, 13. 2. 2008 Naslov: Postano: 22:26 sri, 13. 2. 2008 Naslov: |
    |
|
|
[quote="Spectre"]Evo ti primjer za jednostavnu matricu tipa 4x5 :)
[color=red]2[/color] 4 2 1 -1
0 1 -3 2 0
2 5 -1 5 -1
4 9 1 4 -2
L je uvijek donje trokutasta matrica s [color=purple]1[/color] na dijagonali. Dok primjenjuješ Gaussove eliminacije, u L upisuješ skalare s kojima množiš određeni redak, ali s promjenjenim predznakom. Npr, poćet ćemo s gore označenim brojem [color=red]2[/color]. Očito ćeš drugi redak preskočiti (tj. množiš s [color=green]0[/color] i dodaješ ništa). Za treći redak: množiš prvi red s -1 i dodaješ trećem -> promjena predznaka: [color=brown]1[/color], stavljaš na pripadajuće mjesto u L matricu. Za četvrti redak: množiš prvi red s -2 i dodaješ zadnjem -> promjena predznaka: [color=blue]2[/color], stavljaš na pripadajuće mjesto u L matricu.
Sve to zvuči čudno i ne dovoljno objašnjeno, no zato sam koristio boje :D Dakle, kad provedeš sve moguće Gaussove eliminacije i dobiješ matricu U, matrica L će ovako izgledati:
[color=purple]1[/color] 0 0 0
[color=green]0[/color] [color=purple]1[/color] 0 0
[color=brown]1[/color] 1 [color=purple]1[/color] 0
[color=blue]2[/color] 1 0 [color=purple]1[/color]
A matrica U će biti slijedeća:
2 4 2 1 -1
0 1 -3 2 0
0 0 0 2 0
0 0 0 0 0
r(A) = r(U) = 3
Probaj to rješiti na papiru, trebao bi shvatiti. :)[/quote]
Hvala puno! No kako si dobio one jedinice u 2. stupcu?
Se to uvijek gleda kad "pretvoriš nešto u nulu" na tom mjestu?
| Spectre (napisa): | Evo ti primjer za jednostavnu matricu tipa 4x5 
2 4 2 1 -1
0 1 -3 2 0
2 5 -1 5 -1
4 9 1 4 -2
L je uvijek donje trokutasta matrica s 1 na dijagonali. Dok primjenjuješ Gaussove eliminacije, u L upisuješ skalare s kojima množiš određeni redak, ali s promjenjenim predznakom. Npr, poćet ćemo s gore označenim brojem 2. Očito ćeš drugi redak preskočiti (tj. množiš s 0 i dodaješ ništa). Za treći redak: množiš prvi red s -1 i dodaješ trećem → promjena predznaka: 1, stavljaš na pripadajuće mjesto u L matricu. Za četvrti redak: množiš prvi red s -2 i dodaješ zadnjem → promjena predznaka: 2, stavljaš na pripadajuće mjesto u L matricu.
Sve to zvuči čudno i ne dovoljno objašnjeno, no zato sam koristio boje  Dakle, kad provedeš sve moguće Gaussove eliminacije i dobiješ matricu U, matrica L će ovako izgledati: Dakle, kad provedeš sve moguće Gaussove eliminacije i dobiješ matricu U, matrica L će ovako izgledati:
1 0 0 0
0 1 0 0
1 1 1 0
2 1 0 1
A matrica U će biti slijedeća:
2 4 2 1 -1
0 1 -3 2 0
0 0 0 2 0
0 0 0 0 0
r(A) = r(U) = 3
Probaj to rješiti na papiru, trebao bi shvatiti.  |
Hvala puno! No kako si dobio one jedinice u 2. stupcu?
Se to uvijek gleda kad "pretvoriš nešto u nulu" na tom mjestu?
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
 Postano: 22:36 sri, 13. 2. 2008 Naslov: Postano: 22:36 sri, 13. 2. 2008 Naslov: |
    |
|
|
Pa nakon što provedeš Gaussove eliminacije za tu početnu dvojku, drugi stupac će ti izgledati ovako:
[latex] \left( \begin{array}{c}
4\\
->1<-\\
1\\
1\end{array} \right)[/latex]
Očito, provodiš Gaussove eliminacije po jedinici na mjestu 2,2, u oba slučaja množiš s -1, a kad to promjeni predznak dobiješ 1, kojeg upisuješ u L matricu.
Inače, mi smo to radili tako da odmah na početku napišemo donje trokutastu matricu L s 1 na dijagonali, ali praznim poljima ispod dijagonale, i onda samo dodajemo elemente koje dobivaš tijekom Gaussovih eliminacija. Dakle, na početku imaš samo:
[latex] \left( \begin{array}{cccc}
1 & 0 & 0 & 0 \\
& 1 & 0 & 0 \\
& & 1 & 0\\
& & & 1\end{array} \right)[/latex]
edit: ajd, čak sam se i pomučio te koristio latex :D
Pa nakon što provedeš Gaussove eliminacije za tu početnu dvojku, drugi stupac će ti izgledati ovako:
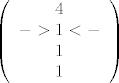
Očito, provodiš Gaussove eliminacije po jedinici na mjestu 2,2, u oba slučaja množiš s -1, a kad to promjeni predznak dobiješ 1, kojeg upisuješ u L matricu.
Inače, mi smo to radili tako da odmah na početku napišemo donje trokutastu matricu L s 1 na dijagonali, ali praznim poljima ispod dijagonale, i onda samo dodajemo elemente koje dobivaš tijekom Gaussovih eliminacija. Dakle, na početku imaš samo:
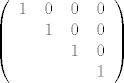
edit: ajd, čak sam se i pomučio te koristio latex 
_________________
Cry havoc, and let loose the dogs of war!
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 10:27 čet, 14. 2. 2008 Naslov: Postano: 10:27 čet, 14. 2. 2008 Naslov: |
    |
|
|
LU faktorizacija primjenjuje se (naročito) i za rješavanje sustava linearnih jednadžbi, jer se rješavanje rastavi u dva jednostavnija koraka:
AX = B, s A = LU,
L(UX) = B
pa se najprije rješava LY = B i onda UX = Y.
Zbog jednostavnosti (trokutastih) matrica sustava L i U, ovi
sustavi sada se lakše rješavaju uzastopnom supstitucijom.
Npr. odmah imamo y1, pa njegovom supstitucijom u drugu jednadžbu y2 itd.
LU faktorizacija primjenjuje se (naročito) i za rješavanje sustava linearnih jednadžbi, jer se rješavanje rastavi u dva jednostavnija koraka:
AX = B, s A = LU,
L(UX) = B
pa se najprije rješava LY = B i onda UX = Y.
Zbog jednostavnosti (trokutastih) matrica sustava L i U, ovi
sustavi sada se lakše rješavaju uzastopnom supstitucijom.
Npr. odmah imamo y1, pa njegovom supstitucijom u drugu jednadžbu y2 itd.
|
|
| [Vrh] |
|
|
















