| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
.bubamara.
Forumaš(ica)
Pridružen/a: 03. 10. 2007. (17:32:18)
Postovi: (4E)16
Spol: 
|
 Postano: 16:00 ned, 20. 4. 2008 Naslov: Re: Nekoliko pitanja... Postano: 16:00 ned, 20. 4. 2008 Naslov: Re: Nekoliko pitanja... |
    |
|
|
[quote="Atomised"]Nevjerojatno glupih. )
1. Je li operator regularan akko mu je matrica regularna ( i ovisi li to o izboru baze)?
2. Je li matrica inverznog operatora jednaka inverzu matrice tog operatora o čijem inverzu pričamo?
3. Kad tražim svojstveni potprostor, dobijem parametarsko rješenje jednadžbe... I sad, kako točno zapisati taj potprostor koji smo dobili?
Kužim da sve to imam negdje u bilješkama, ali... Ali.
Hvala. )[/quote]
1. tak je, operator A iz L(V) je regularan ako i samo ako mu je matrica A(e,e) regularna (ista baza je i u domeni i kodomeni) ;) i regularnost operatora ne ovisi o izboru baze...
2. kad imaš operator A iz L(V) i njegovu matricu A(e,e) (baze su iste!), onda je matrica inverznog operatora jednaka inverzu matrice operatora A
3. kao linearnu ljusku vektora koje si dobio u parametarskom rješenju ;)
;)
[quote="Atomised"]Nevjerojatno glupih. 
1. Je li operator regularan akko mu je matrica regularna ( i ovisi li to o izboru baze)?
2. Je li matrica inverznog operatora jednaka inverzu matrice tog operatora o čijem inverzu pričamo?
3. Kad tražim svojstveni potprostor, dobijem parametarsko rješenje jednadžbe... I sad, kako točno zapisati taj potprostor koji smo dobili?
Kužim da sve to imam negdje u bilješkama, ali... Ali.
Hvala.  [/quote] [/quote]
1. tak je, operator A iz L(V) je regularan ako i samo ako mu je matrica A(e,e) regularna (ista baza je i u domeni i kodomeni)  i regularnost operatora ne ovisi o izboru baze... i regularnost operatora ne ovisi o izboru baze...
2. kad imaš operator A iz L(V) i njegovu matricu A(e,e) (baze su iste!), onda je matrica inverznog operatora jednaka inverzu matrice operatora A
3. kao linearnu ljusku vektora koje si dobio u parametarskom rješenju 

_________________  |
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:26 čet, 1. 5. 2008 Naslov: Postano: 13:26 čet, 1. 5. 2008 Naslov: |
    |
|
|
Ne znam zadatke s kolokvija, ali za ovaj navedeni, ako je točna formulacija, rješenje bi bilo ovakvo: A je singularan, znači ima netrivijalnu jezgru. B možemo definirati tako da na Ker A djeluje kao jedinični operator, a sve izvan jezgre šalje u 0 - to jest, kao operator projekcije na potprostor Ker A. B nije nuloperator jer je Ker A netrivijalna.
Ne znam zadatke s kolokvija, ali za ovaj navedeni, ako je točna formulacija, rješenje bi bilo ovakvo: A je singularan, znači ima netrivijalnu jezgru. B možemo definirati tako da na Ker A djeluje kao jedinični operator, a sve izvan jezgre šalje u 0 - to jest, kao operator projekcije na potprostor Ker A. B nije nuloperator jer je Ker A netrivijalna.
|
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 19:12 čet, 1. 5. 2008 Naslov: Postano: 19:12 čet, 1. 5. 2008 Naslov: |
    |
|
|
Ne razumijem sasvim u čemu je problem, ali evo da pokušam detaljnije napisati. Neka je A singularni operator. Ako je to nul-operator, kompozicija s bilo kojim (pa i različitim od nul-operatora) identički je 0.
Ako A nije nuloperator, ima netrivijalnu jezgru Ker A koja ima svoju bazu. Tu bazu nadopunimo do baze cijelog prostora.
Ako prvo treba djelovati B pa onda A, zadamo B tako da vektore iz baze Ker A šalje same u sebe, a ostale vektore baze prostora šalje u 0.
Na taj način kompozicija je nuloperator.
Ako je zadani poredak u kompoziciji takav da najprije treba djelovati A: kako A šalje one vektore baze prostora koji nisu u Ker A u neke vektore različite od 0, zadamo B tako da sliku od A, Im A, šalje sve u 0, dok vektore baze Ker A šalje svaki u sama sebe. To osigurava da B nije nul-operator, a kompozicija će biti nul-operator.
Ne razumijem sasvim u čemu je problem, ali evo da pokušam detaljnije napisati. Neka je A singularni operator. Ako je to nul-operator, kompozicija s bilo kojim (pa i različitim od nul-operatora) identički je 0.
Ako A nije nuloperator, ima netrivijalnu jezgru Ker A koja ima svoju bazu. Tu bazu nadopunimo do baze cijelog prostora.
Ako prvo treba djelovati B pa onda A, zadamo B tako da vektore iz baze Ker A šalje same u sebe, a ostale vektore baze prostora šalje u 0.
Na taj način kompozicija je nuloperator.
Ako je zadani poredak u kompoziciji takav da najprije treba djelovati A: kako A šalje one vektore baze prostora koji nisu u Ker A u neke vektore različite od 0, zadamo B tako da sliku od A, Im A, šalje sve u 0, dok vektore baze Ker A šalje svaki u sama sebe. To osigurava da B nije nul-operator, a kompozicija će biti nul-operator.
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Gost
|
 Postano: 16:50 uto, 6. 5. 2008 Naslov: Postano: 16:50 uto, 6. 5. 2008 Naslov: |
    |
|
|
Općenito preslikavanjem bilo koje baze prostora V dobivamo skup izvodnica slike A(V) = Im A, kako se već označi - to je prilično očito, jer element slike je linearna kombinacija slika vektora baze. U ovom kontekstu, kako je baza sastavljena tako da prvih d vektora pripadaju jezgri, slika svakog od njih je 0. Zato se svaki Ax može napisati kao lin. kombinacija preostalih n-d vektora izabrane baze. (Prvih d vektora baze "ne daju ništa", tj samo 0).
Nadalje, jedini vektor koji pripada i nekom potprostoru i njegovom direktnom komplementu jest 0. Općenito, bilo koji lin. nezavisni podskup i njegova nadopuna do baze prostora razapinju potprostore koji su uzajamno direktni komplementi (tako se općenito i dobiva direktni komplement potprostora - uzme se baza tog potprostora i nadopuni do baze prostora itd). To je gotovo trivijalno. U ovom slučaju, potprostor o kojem je riječ jest jezgra lin. operatora.
Općenito preslikavanjem bilo koje baze prostora V dobivamo skup izvodnica slike A(V) = Im A, kako se već označi - to je prilično očito, jer element slike je linearna kombinacija slika vektora baze. U ovom kontekstu, kako je baza sastavljena tako da prvih d vektora pripadaju jezgri, slika svakog od njih je 0. Zato se svaki Ax može napisati kao lin. kombinacija preostalih n-d vektora izabrane baze. (Prvih d vektora baze "ne daju ništa", tj samo 0).
Nadalje, jedini vektor koji pripada i nekom potprostoru i njegovom direktnom komplementu jest 0. Općenito, bilo koji lin. nezavisni podskup i njegova nadopuna do baze prostora razapinju potprostore koji su uzajamno direktni komplementi (tako se općenito i dobiva direktni komplement potprostora - uzme se baza tog potprostora i nadopuni do baze prostora itd). To je gotovo trivijalno. U ovom slučaju, potprostor o kojem je riječ jest jezgra lin. operatora.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 21:11 ned, 18. 5. 2008 Naslov: Postano: 21:11 ned, 18. 5. 2008 Naslov: |
    |
|
|
ti vektori jesu čudni, ali tako su definirani da bi dokaz bio takav kakav je. :silly:
pokazujemo:
[latex](f_{j+1}|e_i)=0[/latex], [latex]\forall i=1,...,j[/latex].
fiksiraj [latex]i[/latex]:
[latex](f_{j+1}|e_i)= \\* =(x_{j+1} - \sum_{k=1}^j (x_{j+1}|e_k)e_k = \\* = (x_{j+1}|e_i) - \sum_{k=1}^j (x_{j+1}|e_k)(e_k|e_i) = \\* = (x_{j+1}|e_i) - (x_{j+1}|e_i) \cdot 1[/latex]
u zadnjoj sumi preživi samo [latex](x_{j+1}|e_i)(e_i|e_i)[/latex], jer je za [latex]k \neq i, \hspace{2 mm} (e_k|e_i)=0[/latex].
:violin:
ti vektori jesu čudni, ali tako su definirani da bi dokaz bio takav kakav je. 
pokazujemo:
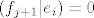 , , 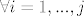 . .
fiksiraj  : :
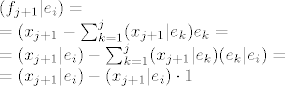
u zadnjoj sumi preživi samo 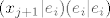 , jer je za , jer je za 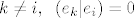 . .

_________________
ima let u finish
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 21:26 ned, 18. 5. 2008 Naslov: Postano: 21:26 ned, 18. 5. 2008 Naslov: |
    |
|
|
[quote="ma"]ti vektori jesu čudni, ali tako su definirani da bi dokaz bio takav kakav je. :silly:
pokazujemo:
[latex](f_{j+1}|e_i)=0[/latex], [latex]\forall i=1,...,j[/latex].
fiksiraj [latex]i[/latex]:
[latex](f_{j+1}|e_i)= \\* =(x_{j+1} - \sum_{k=1}^j (x_{j+1}|e_k)e_k = \\* = (x_{j+1}|e_i) - \sum_{k=1}^j (x_{j+1}|e_k)(e_k|e_i) = \\* = (x_{j+1}|e_i) - (x_{j+1}|e_i) \cdot 1[/latex]
u zadnjoj sumi preživi samo [latex](x_{j+1}|e_i)(e_i|e_i)[/latex], jer je za [latex]k \neq i, \hspace{2 mm} (e_k|e_i)=0[/latex].
:violin:[/quote]
Hvala. :D
| ma (napisa): | ti vektori jesu čudni, ali tako su definirani da bi dokaz bio takav kakav je. 
pokazujemo:
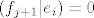 , , 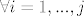 . .
fiksiraj  : :
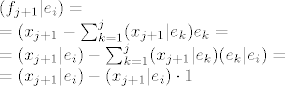
u zadnjoj sumi preživi samo 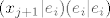 , jer je za , jer je za 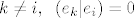 . .
 |
Hvala. 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 15:16 sub, 24. 5. 2008 Naslov: Postano: 15:16 sub, 24. 5. 2008 Naslov: |
    |
|
|
[quote="Atomised"]Kako se pomoću svojstvenog polinoma invertira matrica? :D[/quote]
ovako :D nađeš svojstveni polinom, i po hamilton-cayleyovom teoremu vrijedi da je k[size=9]A[/size](A)=0( nul-matrica), i to lijepo uvrstiš unutra( i ne zaboravi slobodni član pomnožit s I ;) ) e sad, na jednoj strani ostaviš samo I, na drugu prebaci sve ostalo, i od tamo izluči A, pa ćeš tako dobit izraz oblika I=A*nešto, i to je nešto što ti ostane je upravo A^(-1)... valjda je jasno :)
| Atomised (napisa): | Kako se pomoću svojstvenog polinoma invertira matrica?  |
ovako  nađeš svojstveni polinom, i po hamilton-cayleyovom teoremu vrijedi da je kA(A)=0( nul-matrica), i to lijepo uvrstiš unutra( i ne zaboravi slobodni član pomnožit s I nađeš svojstveni polinom, i po hamilton-cayleyovom teoremu vrijedi da je kA(A)=0( nul-matrica), i to lijepo uvrstiš unutra( i ne zaboravi slobodni član pomnožit s I  ) e sad, na jednoj strani ostaviš samo I, na drugu prebaci sve ostalo, i od tamo izluči A, pa ćeš tako dobit izraz oblika I=A*nešto, i to je nešto što ti ostane je upravo A^(-1)... valjda je jasno ) e sad, na jednoj strani ostaviš samo I, na drugu prebaci sve ostalo, i od tamo izluči A, pa ćeš tako dobit izraz oblika I=A*nešto, i to je nešto što ti ostane je upravo A^(-1)... valjda je jasno 
_________________ kalendar 
  |
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 15:23 sub, 24. 5. 2008 Naslov: Postano: 15:23 sub, 24. 5. 2008 Naslov: |
    |
|
|
[quote="arya"][quote="Atomised"]Kako se pomoću svojstvenog polinoma invertira matrica? :D[/quote]
ovako :D nađeš svojstveni polinom, i po hamilton-cayleyovom teoremu vrijedi da je k[size=9]A[/size](A)=0( nul-matrica), i to lijepo uvrstiš unutra( i ne zaboravi slobodni član pomnožit s I ;) ) e sad, na jednoj strani ostaviš samo I, na drugu prebaci sve ostalo, i od tamo izluči A, pa ćeš tako dobit izraz oblika I=A*nešto, i to je nešto što ti ostane je upravo A^(-1)... valjda je jasno :)[/quote]
Hvala. :D Jasno je. :)
| arya (napisa): | | Atomised (napisa): | Kako se pomoću svojstvenog polinoma invertira matrica?  |
ovako  nađeš svojstveni polinom, i po hamilton-cayleyovom teoremu vrijedi da je kA(A)=0( nul-matrica), i to lijepo uvrstiš unutra( i ne zaboravi slobodni član pomnožit s I nađeš svojstveni polinom, i po hamilton-cayleyovom teoremu vrijedi da je kA(A)=0( nul-matrica), i to lijepo uvrstiš unutra( i ne zaboravi slobodni član pomnožit s I  ) e sad, na jednoj strani ostaviš samo I, na drugu prebaci sve ostalo, i od tamo izluči A, pa ćeš tako dobit izraz oblika I=A*nešto, i to je nešto što ti ostane je upravo A^(-1)... valjda je jasno ) e sad, na jednoj strani ostaviš samo I, na drugu prebaci sve ostalo, i od tamo izluči A, pa ćeš tako dobit izraz oblika I=A*nešto, i to je nešto što ti ostane je upravo A^(-1)... valjda je jasno  |
Hvala.  Jasno je. Jasno je. 
|
|
| [Vrh] |
|
|










