| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Janko
Forumaš(ica)

Pridružen/a: 02. 05. 2008. (18:33:24)
Postovi: (4)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Janko
Forumaš(ica)

Pridružen/a: 02. 05. 2008. (18:33:24)
Postovi: (4)16
|
 Postano: 1:34 sub, 3. 5. 2008 Naslov: Postano: 1:34 sub, 3. 5. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Za početak, škicni [url=http://degiorgi.math.hr/forum/viewtopic.php?t=10335]TU[/url]
A sad pomoć:
prvi konvergira preko Leibnizovog kriterija
drugi rastaviš na 1/n + 3/n^2 pa pošto prvi divergira, divergira cijeli
treci rastaviš na parc razlomke pa dobiješ dva skoro pa 1/n koji divergiraju.
Nek me netko ispravi ak sam napiso neku glupost.
I pitaj ako nešto nije jasno ili treba raspisat neki korak... ;)[/quote]
hehhe.. e care, ako me kontas, ja sam ti totalno neuk za matku.. pa ako ti nije problem da mi to malo raspises, i objasnis kako da ja to napisem, bio bih ti dozivotno zahvalan, placam cugu, ukrajinke, sto god treba.. :) :)
fakat ne kuzim, jer mi to nismo nikad radili, a sad mi dali esej iz toga, i nikako da skontam to..
| Luuka (napisa): | Za početak, škicni TU
A sad pomoć:
prvi konvergira preko Leibnizovog kriterija
drugi rastaviš na 1/n + 3/n^2 pa pošto prvi divergira, divergira cijeli
treci rastaviš na parc razlomke pa dobiješ dva skoro pa 1/n koji divergiraju.
Nek me netko ispravi ak sam napiso neku glupost.
I pitaj ako nešto nije jasno ili treba raspisat neki korak...  |
hehhe.. e care, ako me kontas, ja sam ti totalno neuk za matku.. pa ako ti nije problem da mi to malo raspises, i objasnis kako da ja to napisem, bio bih ti dozivotno zahvalan, placam cugu, ukrajinke, sto god treba..  
fakat ne kuzim, jer mi to nismo nikad radili, a sad mi dali esej iz toga, i nikako da skontam to..
|
|
| [Vrh] |
|
Janko
Forumaš(ica)

Pridružen/a: 02. 05. 2008. (18:33:24)
Postovi: (4)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:12 sub, 3. 5. 2008 Naslov: Postano: 21:12 sub, 3. 5. 2008 Naslov: |
    |
|
|
Strpljenja, strpljenja... ;)
A ovak nekak:
1. pogledaj što kaže Leibnitzov kriterij. Mi imamo [latex]\sum{(-1)^{n+1} \frac{1}{n}}[/latex] Izlučimo -1 pa imamo [latex] - \sum{(-1)^{n} \frac{1}{n}}[/latex]. Naš an je ovaj 1/n. To je padajuć niz s pozitivnim elementima (an>0) , i lim an=0. Sad po Leibnitzovom kriteriju ovaj red (ne 1/n, nego sa onim (-1)^n ) konvergira.
2. [latex]\sum{ \frac {n+3}{n^2}}= \sum{\frac{1}{n}} + 3 \sum{\frac{1}{n^2}}[/latex] (kad se rastavi brojnik i 3 ode ispred sume). Ovaj drugi red divergira ( ovaj 1/n ) pa onda i početni red divergira. (za 1/n se lako, integralnim kriterijem provjeri da divergira, naime [latex]\sum{\frac{1}{n}}[/latex] divergira ako i samo ako [latex]\int_{1}^{\infty}{\frac{1}{n}dn}[/latex] divergira. A ovaj integral je ln n od 1 do beskonačno, što divergira)
3. [latex]\sum{\frac{1}{n^2-1}}=\frac{1}{2} \sum{ \frac{1}{n+1}} - \frac{1}{2} \sum{\frac{1}{n-1}}[/latex]. (tu smo koristili rastav na parcijalne razlomke) Ova dva reda, jako sliče onom 1/n koji divergira, a na njega se našima tak da sumacija kreće od drugog indexa, a pošto nisam nigdje piso indexe u sumi, samo nek bude da ovi dva divergiraju jer 1/n divergira.
I to je to. 8)
P.s. Pogledaj i [url=http://web.math.hr/nastava/analiza/dodatni.html]TU[/url]. Imaš skriptu i još nekih primjera... :D
Strpljenja, strpljenja... 
A ovak nekak:
1. pogledaj što kaže Leibnitzov kriterij. Mi imamo 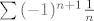 Izlučimo -1 pa imamo Izlučimo -1 pa imamo 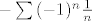 . Naš an je ovaj 1/n. To je padajuć niz s pozitivnim elementima (an>0) , i lim an=0. Sad po Leibnitzovom kriteriju ovaj red (ne 1/n, nego sa onim (-1)^n ) konvergira. . Naš an je ovaj 1/n. To je padajuć niz s pozitivnim elementima (an>0) , i lim an=0. Sad po Leibnitzovom kriteriju ovaj red (ne 1/n, nego sa onim (-1)^n ) konvergira.
2. 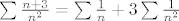 (kad se rastavi brojnik i 3 ode ispred sume). Ovaj drugi red divergira ( ovaj 1/n ) pa onda i početni red divergira. (za 1/n se lako, integralnim kriterijem provjeri da divergira, naime (kad se rastavi brojnik i 3 ode ispred sume). Ovaj drugi red divergira ( ovaj 1/n ) pa onda i početni red divergira. (za 1/n se lako, integralnim kriterijem provjeri da divergira, naime 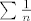 divergira ako i samo ako divergira ako i samo ako 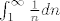 divergira. A ovaj integral je ln n od 1 do beskonačno, što divergira) divergira. A ovaj integral je ln n od 1 do beskonačno, što divergira)
3. 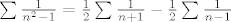 . (tu smo koristili rastav na parcijalne razlomke) Ova dva reda, jako sliče onom 1/n koji divergira, a na njega se našima tak da sumacija kreće od drugog indexa, a pošto nisam nigdje piso indexe u sumi, samo nek bude da ovi dva divergiraju jer 1/n divergira. . (tu smo koristili rastav na parcijalne razlomke) Ova dva reda, jako sliče onom 1/n koji divergira, a na njega se našima tak da sumacija kreće od drugog indexa, a pošto nisam nigdje piso indexe u sumi, samo nek bude da ovi dva divergiraju jer 1/n divergira.
I to je to. 
P.s. Pogledaj i TU. Imaš skriptu i još nekih primjera... 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
 Postano: 21:27 sub, 3. 5. 2008 Naslov: Postano: 21:27 sub, 3. 5. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Strpljenja, strpljenja... ;)
3. [latex]\sum{\frac{1}{n^2-1}}=\frac{1}{2} \sum{ \frac{1}{n+1}} - \frac{1}{2} \sum{\frac{1}{n-1}}[/latex]. (tu smo koristili rastav na parcijalne razlomke) Ova dva reda, jako sliče onom 1/n koji divergira, a na njega se našima tak da sumacija kreće od drugog indexa, a pošto nisam nigdje piso indexe u sumi, samo nek bude da ovi dva divergiraju jer 1/n divergira.
[/quote]
:shock: :shock: :shock: :shock: :shock: :shock:
Luuka!! :)
neee nenenene :D
ovaj red poprilicno konvergira :)
kao prvo rastav ti je naopacke..
kao drugo, svi ti pribrojnici ti se pokrate. ostanu ti samo prva dva(ocito da kreces od n=2 jer za n=1 prvi clan nije definiran) pa je red konvergentan sa sumom 1/2(1/1+1/2)=3/4
| Luuka (napisa): | Strpljenja, strpljenja... 
3. 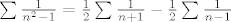 . (tu smo koristili rastav na parcijalne razlomke) Ova dva reda, jako sliče onom 1/n koji divergira, a na njega se našima tak da sumacija kreće od drugog indexa, a pošto nisam nigdje piso indexe u sumi, samo nek bude da ovi dva divergiraju jer 1/n divergira. . (tu smo koristili rastav na parcijalne razlomke) Ova dva reda, jako sliče onom 1/n koji divergira, a na njega se našima tak da sumacija kreće od drugog indexa, a pošto nisam nigdje piso indexe u sumi, samo nek bude da ovi dva divergiraju jer 1/n divergira.
|
     
Luuka!! 
neee nenenene 
ovaj red poprilicno konvergira 
kao prvo rastav ti je naopacke..
kao drugo, svi ti pribrojnici ti se pokrate. ostanu ti samo prva dva(ocito da kreces od n=2 jer za n=1 prvi clan nije definiran) pa je red konvergentan sa sumom 1/2(1/1+1/2)=3/4
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Janko
Forumaš(ica)

Pridružen/a: 02. 05. 2008. (18:33:24)
Postovi: (4)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 20:58 pon, 5. 5. 2008 Naslov: Postano: 20:58 pon, 5. 5. 2008 Naslov: |
    |
|
|
Jedna nebitna, formalna stvar, [latex]\sum\limits_{n \geqslant 2} {\frac{1}
{{n^2 - 1}}} = \sum\limits_{n \geqslant 2} {\left( {\frac{1}
{2}\frac{1}
{{n - 1}} - \frac{1}
{2}\frac{1}
{{n + 1}}} \right)} = \frac{1}
{2}\left( {1 + \frac{1}
{2}} \right) + \sum\limits_{n \geqslant 2} {\left( {\frac{1}
{2}\frac{1}
{{n + 1}} - \frac{1}
{2}\frac{1}
{{n + 1}}} \right)} = \frac{3}
{4}[/latex], a ne [latex]\sum\limits_{n \geqslant 2} {\frac{1}
{{n^2 - 1}}} \ne \frac{1}
{2}\sum\limits_{n \geqslant 2} {\frac{1}
{{n - 1}}} - \frac{1}
{2}\sum\limits_{n \geqslant 2} {\frac{1}
{{n + 1}}} = \infty - \infty = ?[/latex]. Dobro, ne baš tolko nebitna, treba imat na umu da je suma reda granični postupak, a ne beskonačno mnogo komada koje sparujemo kak god hoćemo
Jedna nebitna, formalna stvar, 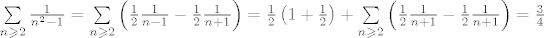 , a ne , a ne 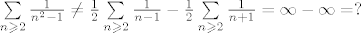 . Dobro, ne baš tolko nebitna, treba imat na umu da je suma reda granični postupak, a ne beskonačno mnogo komada koje sparujemo kak god hoćemo . Dobro, ne baš tolko nebitna, treba imat na umu da je suma reda granični postupak, a ne beskonačno mnogo komada koje sparujemo kak god hoćemo
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
|






