| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gloryt
Forumaš(ica)

Pridružen/a: 08. 03. 2008. (11:30:40)
Postovi: (B)16
|
|
| [Vrh] |
|
gloryt
Forumaš(ica)

Pridružen/a: 08. 03. 2008. (11:30:40)
Postovi: (B)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:51 sub, 10. 5. 2008 Naslov: Re: Sinusoida za po doma Postano: 0:51 sub, 10. 5. 2008 Naslov: Re: Sinusoida za po doma |
    |
|
|
[quote="gloryt"]Dakle imam osnovnu (crvenu) y1=sinX
Dakle, očigledno je da je u ovom slučaju uvijek za bilo koji X: y2<y1[/quote]
Preciznije, ako je [latex]f(x)=\sin{x}[/latex], a [latex]g(x)=\sin{x}-y_3,~y_3 \in \left\langle 0 , +\infty \right\rangle[/latex], tada je [latex]g(x)< f(x)~\forall x \in \mathbb{R}[/latex]
[quote]nemoguće da umjesto y3 imam konstantu (možda nisam dobro nacrtao ovaj graf pa nije odmah uočljivo) jer ako je y3 konstanta - ne bih imao pravu "paralelnost". [/quote]
y3 mora biti konstanta jer f(x)-g(x) je baš jednako y3 za svaki x.
[quote]Dakle "plava" funkcija mi je y2=sinX minus "nešto" i molio bih kad bi mi netko mogao pomoći definirati to "nešto". Ja sam ga na slici nazvao y3.[/quote]
To nešto je pozitivan realan broj. Može biti i negativan, samo onda slika drugačije izgleda, plavi graf dolazi iznad crvenog.
Lako možeš eksperimentirati s nekim programom za crtanje grafova. [url=http://www.geogebra.org/cms/]Geogebra[/url] je freeware program u kojemu se može nacrtati graf funkcije sinus. Jednostavno nacrtaj sin x i onda nacrtaj npr. sinx + 1 pa sinx - 1 i gledaj što se dešava.
U attachmentu sam ti stavio geogebra file (prvo moraš unrar napravit jer forum ne podržava ggb ekstenziju) koji će ti pokazati funkcije sinx i sinx - a, a broj a možeš mijenjati klizačem u gornjem desnom kutu. Isprobaj pa vidi što se dešava.
| gloryt (napisa): | Dakle imam osnovnu (crvenu) y1=sinX
Dakle, očigledno je da je u ovom slučaju uvijek za bilo koji X: y2<y1 |
Preciznije, ako je 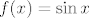 , a , a 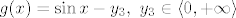 , tada je , tada je 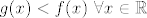
| Citat: | | nemoguće da umjesto y3 imam konstantu (možda nisam dobro nacrtao ovaj graf pa nije odmah uočljivo) jer ako je y3 konstanta - ne bih imao pravu "paralelnost". |
y3 mora biti konstanta jer f(x)-g(x) je baš jednako y3 za svaki x.
| Citat: | | Dakle "plava" funkcija mi je y2=sinX minus "nešto" i molio bih kad bi mi netko mogao pomoći definirati to "nešto". Ja sam ga na slici nazvao y3. |
To nešto je pozitivan realan broj. Može biti i negativan, samo onda slika drugačije izgleda, plavi graf dolazi iznad crvenog.
Lako možeš eksperimentirati s nekim programom za crtanje grafova. Geogebra je freeware program u kojemu se može nacrtati graf funkcije sinus. Jednostavno nacrtaj sin x i onda nacrtaj npr. sinx + 1 pa sinx - 1 i gledaj što se dešava.
U attachmentu sam ti stavio geogebra file (prvo moraš unrar napravit jer forum ne podržava ggb ekstenziju) koji će ti pokazati funkcije sinx i sinx - a, a broj a možeš mijenjati klizačem u gornjem desnom kutu. Isprobaj pa vidi što se dešava.
_________________
The Dude Abides
| Description: |
|

Download |
| Filename: |
sinus.rar |
| Filesize: |
1013 Bytes |
| Downloaded: |
101 Time(s) |
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 1:30 sub, 10. 5. 2008 Naslov: Postano: 1:30 sub, 10. 5. 2008 Naslov: |
    |
|
|
[latex]B = \left( {x_0 ,\sin x_0 } \right)[/latex] proizvoljna točka na sinusoidi i [latex]B' = \left( {x_1 ,y\left( {x_1 } \right)} \right)[/latex]. Jednadžba normale na [latex]y_1[/latex] u točki [latex]x_0[/latex] je dana sa [latex] - \cos x_0 \left( {y - \sin x_0 } \right) = x - x_0[/latex], posebno i [latex]{B'}[/latex] leži na njoj pa zadovoljava njenu jednadžbu pa vrijedi [latex] - \cos x_0 \left( {y\left( {x_1 } \right) - \sin x_0 } \right) = x_1 - x_0[/latex]. Udaljenost [latex]d\left( {B,B'} \right) = d[/latex] je konstantna pa imamo [latex]\sqrt {\left( {x_1 - x_0 } \right)^2 + \left( {y\left( {x_1 } \right) - \sin x_0 } \right)^2 } = d[/latex] odakle slijedi [latex]y\left( {x_1 \left( {x_0 } \right)} \right) = \sin x_0 - \frac{d}
{{\sqrt {1 + \cos ^2 x_0 } }}[/latex]. Deriviranjem po [latex]x_0[/latex] dobivamo [latex]y'\left( {x_1 \left( {x_0 } \right)} \right)x'_1 \left( {x_0 } \right) = \cos x_0 x'_1 \left( {x_0 } \right) = \cos x_0 - \frac{{d\cos x_0 \sin x_0 }}
{{\left( {1 + \cos ^2 x_0 } \right)^{\frac{3}
{2}} }}[/latex]
([latex]y'\left( {x_1 \left( {x_0 } \right)} \right) = \left( {\sin \left( {x_0 } \right)} \right)^\prime = \cos x_0[/latex] zbog zahtjeva paralelnosti). Odavde slijedi (ne djeljenjem sa [latex]\cos x_0[/latex], ali ipak slijedi) [latex]x'_1 \left( {x_0 } \right) = 1 - \frac{{d\sin x_0 }}
{{\left( {1 + \cos ^2 x_0 } \right)^{\frac{3}
{2}} }}[/latex] odakle se rješavanjem diferencijalne jednadžbe koja je separabilna i zadovoljava uvjete teorema [url]http://web.math.hr/nastava/odif/predavanja/separ.pdf[/url] na prvoj stranici uz [latex]\left| d \right| < 1[/latex] s inicijalnim uvjetom [latex]x_1 \left( {\frac{\pi }
{2}} \right) = \frac{\pi }
{2}[/latex] dobiva [latex]x_1 \left( {x_0 } \right) = x_0 + \frac{{d\cos x_0 }}
{{\sqrt {1 + \cos ^2 x_0 } }}[/latex] što je bijekcija pa ima inverz, tj. postoji funkcija za koju vrijedi [latex]f\left( {x_1 } \right) = x_0[/latex] pa je tražena jednadžba [latex]y\left( {x_1 } \right) = \sin \left( {f\left( {x_1 } \right)} \right) - \frac{d}
{{\sqrt {1 + \cos ^2 \left( {f\left( {x_1 } \right)} \right)} }}[/latex]. [latex]f:\mathbb{R} \to \mathbb{R}[/latex] je inverz funkcije [latex]x_1 :\mathbb{R} \to \mathbb{R}[/latex], [latex]x_1 \left( {x_0 } \right) = x_0 + \frac{{d\cos x_0 }}
{{\sqrt {1 + \cos ^2 x_0 } }}[/latex] koji, iako ne vidim neki način da ga eksplicitno izrazim, je pravilno zadana funkcija. Lako se vidi da za [latex]\left| d \right| > 1[/latex] problem nema rješenje.
Dakle ono što si označio sa [latex]y_2[/latex] ima ovu jednadžbu gore, ne izgleda baš ko sinusoida. Ak pomaže, Taylorov razvof od [latex]f[/latex] oko [latex]\frac{d}
{{\sqrt 2 }}[/latex] počinje sa [latex]f\left( {x_1 } \right) \approx \left( {x_1 - \frac{d}
{{\sqrt 2 }}} \right) + \frac{d}
{{4\sqrt 2 }}\left( {x - \frac{d}
{{\sqrt 2 }}} \right)^2 + \frac{{d^2 }}
{{16}}\left( {x - \frac{d}
{{\sqrt 2 }}} \right)^3[/latex]
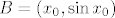 proizvoljna točka na sinusoidi i proizvoljna točka na sinusoidi i 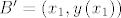 . Jednadžba normale na . Jednadžba normale na 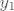 u točki u točki  je dana sa je dana sa 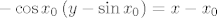 , posebno i , posebno i 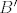 leži na njoj pa zadovoljava njenu jednadžbu pa vrijedi leži na njoj pa zadovoljava njenu jednadžbu pa vrijedi 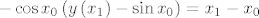 . Udaljenost . Udaljenost 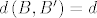 je konstantna pa imamo je konstantna pa imamo  odakle slijedi odakle slijedi 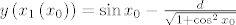 . Deriviranjem po . Deriviranjem po  dobivamo dobivamo 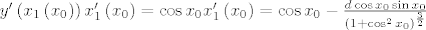
(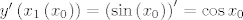 zbog zahtjeva paralelnosti). Odavde slijedi (ne djeljenjem sa zbog zahtjeva paralelnosti). Odavde slijedi (ne djeljenjem sa 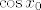 , ali ipak slijedi) , ali ipak slijedi) 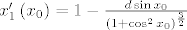 odakle se rješavanjem diferencijalne jednadžbe koja je separabilna i zadovoljava uvjete teorema http://web.math.hr/nastava/odif/predavanja/separ.pdf na prvoj stranici uz odakle se rješavanjem diferencijalne jednadžbe koja je separabilna i zadovoljava uvjete teorema http://web.math.hr/nastava/odif/predavanja/separ.pdf na prvoj stranici uz  s inicijalnim uvjetom s inicijalnim uvjetom 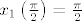 dobiva dobiva 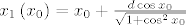 što je bijekcija pa ima inverz, tj. postoji funkcija za koju vrijedi što je bijekcija pa ima inverz, tj. postoji funkcija za koju vrijedi 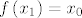 pa je tražena jednadžba pa je tražena jednadžba 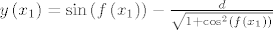 . . 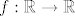 je inverz funkcije je inverz funkcije 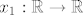 , , 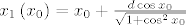 koji, iako ne vidim neki način da ga eksplicitno izrazim, je pravilno zadana funkcija. Lako se vidi da za koji, iako ne vidim neki način da ga eksplicitno izrazim, je pravilno zadana funkcija. Lako se vidi da za  problem nema rješenje. problem nema rješenje.
Dakle ono što si označio sa 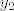 ima ovu jednadžbu gore, ne izgleda baš ko sinusoida. Ak pomaže, Taylorov razvof od ima ovu jednadžbu gore, ne izgleda baš ko sinusoida. Ak pomaže, Taylorov razvof od  oko oko 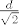 počinje sa počinje sa 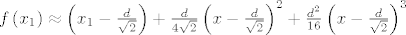
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 19:22 sub, 2. 8. 2008; ukupno mijenjano 8 put/a.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 3:51 sub, 10. 5. 2008 Naslov: Postano: 3:51 sub, 10. 5. 2008 Naslov: |
    |
|
|
[quote="alen"]Dakle ono što si označio sa [latex]y_2[/latex] ima ovu jednadžbu gore, ne izgleda baš ko sinusoida.[/quote]
Niti y1 ne izgleda kao sinusoida, udaljenost maksimuma do x-osi je manja od udaljenosti minimuma do x-osi.
[quote="alen"]Razlika nije konstanta jer je zadan uvjet da je udaljenost između točaka na normali konstantna, a tangente u tim točkama paralelne.[/quote]
Gdje je to zadano? Ako bi udaljenost između točaka na normali bila konstantna, tada dobiveni graf ne bi bio graf funkcije, tj. postojala bi barem jedna točka x koju y2 šalje u dvije vrijednosti.
Koliko sam ja shvatio, zadani su y1 i y2 i traži se y3 takav da prenese plavi graf čija je jednadžba g(x)=sinx - y3 u crveni čija je jednadžba f(x)=sinx. Sa slike je očito da je za svaki x f(x)-g(x) konstantna vrijednost upravo jednaka y3.
| alen (napisa): | Dakle ono što si označio sa 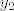 ima ovu jednadžbu gore, ne izgleda baš ko sinusoida. ima ovu jednadžbu gore, ne izgleda baš ko sinusoida. |
Niti y1 ne izgleda kao sinusoida, udaljenost maksimuma do x-osi je manja od udaljenosti minimuma do x-osi.
| alen (napisa): | | Razlika nije konstanta jer je zadan uvjet da je udaljenost između točaka na normali konstantna, a tangente u tim točkama paralelne. |
Gdje je to zadano? Ako bi udaljenost između točaka na normali bila konstantna, tada dobiveni graf ne bi bio graf funkcije, tj. postojala bi barem jedna točka x koju y2 šalje u dvije vrijednosti.
Koliko sam ja shvatio, zadani su y1 i y2 i traži se y3 takav da prenese plavi graf čija je jednadžba g(x)=sinx - y3 u crveni čija je jednadžba f(x)=sinx. Sa slike je očito da je za svaki x f(x)-g(x) konstantna vrijednost upravo jednaka y3.
_________________
The Dude Abides
Zadnja promjena: goranm; 4:10 sub, 10. 5. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
gloryt
Forumaš(ica)

Pridružen/a: 08. 03. 2008. (11:30:40)
Postovi: (B)16
|
 Postano: 9:52 sub, 10. 5. 2008 Naslov: Postano: 9:52 sub, 10. 5. 2008 Naslov: |
    |
|
|
[quote="goranm"][quote="gloryt"]Duljina dužine AA' jednaka je BB'[/quote]Zašto je to tako? Da li se to predpostavlja u zadatku ili si zaključio to iz nečega (a ako jesi, iz čega?) :)[/quote]
Prvo hvala svima na trudu. Samo da razjasnim nešto pa ću onda iskomentirati ostale postove.
Ovo što sam nacrtao gore u "zadatku" je nacrtano CorelDraw-om u minut-dva, tako da možda nisam nacrtao "pravu" sinusoidu, ali zamislite da jest i da su maksimumi jednaki ispod i iznad x-osi - što na slici možda nije. (Nisam mislio da ćete to uočiti.) :shock:
Duljine dužina AA' i BB' su jednake jer ja želim da tako bude. Ja pokušavam definirati dvije sinusoide. Prva je y=sinX i to je jasno ko dan, ali problem je druga (plava) ali takva da AA' i BB' između njih uvijek budu jednaki. Dakle to je "moj" uvjet.
@goranm:
[quote]y3 mora biti konstanta jer f(x)-g(x) je baš jednako y3 za svaki x.[/quote]
Alen je dobro odgovorio. Ja ne želim konstantu jer neću dobiti dva potpuno "paralelna" grafa funkcije. Pogledaj sliku. Ovdje sam zadao da je y3=const, odnosno da je y3=1. Gledaj što dobijem:
[img]http://i28.tinypic.com/wstch3.jpg[/img]
AA'=BB' ali nije jednako RR'. Međutim RR'=SS' i ja želim da moj graf funkcije prolazi kroz S' (vidi iscrtkani dio grafa). Dakle, tangenta na y1 u točki R mora biti paralelna s tangentom na y2 u točki R'. Kužiš? Samo sam ja malo zakomplicirao objašnjenje jer nisam matematičar niti ću kada biti. :?
Ako imam y3 kao konstantu - onda udaljenost između tih točki nije jednaka, a ja želim definirati tu varijablu.
| goranm (napisa): | | gloryt (napisa): | | Duljina dužine AA' jednaka je BB' |
Zašto je to tako? Da li se to predpostavlja u zadatku ili si zaključio to iz nečega (a ako jesi, iz čega?)  |
Prvo hvala svima na trudu. Samo da razjasnim nešto pa ću onda iskomentirati ostale postove.
Ovo što sam nacrtao gore u "zadatku" je nacrtano CorelDraw-om u minut-dva, tako da možda nisam nacrtao "pravu" sinusoidu, ali zamislite da jest i da su maksimumi jednaki ispod i iznad x-osi - što na slici možda nije. (Nisam mislio da ćete to uočiti.) 
Duljine dužina AA' i BB' su jednake jer ja želim da tako bude. Ja pokušavam definirati dvije sinusoide. Prva je y=sinX i to je jasno ko dan, ali problem je druga (plava) ali takva da AA' i BB' između njih uvijek budu jednaki. Dakle to je "moj" uvjet.
@goranm:
| Citat: | | y3 mora biti konstanta jer f(x)-g(x) je baš jednako y3 za svaki x. |
Alen je dobro odgovorio. Ja ne želim konstantu jer neću dobiti dva potpuno "paralelna" grafa funkcije. Pogledaj sliku. Ovdje sam zadao da je y3=const, odnosno da je y3=1. Gledaj što dobijem:

AA'=BB' ali nije jednako RR'. Međutim RR'=SS' i ja želim da moj graf funkcije prolazi kroz S' (vidi iscrtkani dio grafa). Dakle, tangenta na y1 u točki R mora biti paralelna s tangentom na y2 u točki R'. Kužiš? Samo sam ja malo zakomplicirao objašnjenje jer nisam matematičar niti ću kada biti. 
Ako imam y3 kao konstantu - onda udaljenost između tih točki nije jednaka, a ja želim definirati tu varijablu.
|
|
| [Vrh] |
|
gloryt
Forumaš(ica)

Pridružen/a: 08. 03. 2008. (11:30:40)
Postovi: (B)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 12:53 sub, 10. 5. 2008 Naslov: Postano: 12:53 sub, 10. 5. 2008 Naslov: |
    |
|
|
[quote="goranm"]Gdje je to zadano? Ako bi udaljenost između točaka na normali bila konstantna, tada dobiveni graf ne bi bio graf funkcije, tj. postojala bi barem jedna točka x koju y2 šalje u dvije vrijednosti.[/quote]
Gore iz računa se vidi da se ta situacija dešava samo kada zahtjevamo da je udaljenost veća od 1. Ako je manja od jedan tada se radi o sasvim pravilno zadanoj funkciji (imamo ograničenje da tražena funkcija mora biti ispod grafa sinusoide).
[quote]Prvo moram pomno proučiti tvoj post i malo eksperimentirati, pa tek onda odgovoriti iako me malo bode u oči ovaj korijen u nazivniku (automatski nema rješenje u nekoj točki). [/quote]
Vrijednost pod korijenom je uvijek veća ili jednaka jedan, tak da je to definirano u svim točkama (automatski je i cijeli nazivnik veći ili jednak jedan).
[quote]Niti y1 ne izgleda kao sinusoida, udaljenost maksimuma do x-osi je manja od udaljenosti minimuma do x-osi. [/quote]
[quote]Ovo što sam nacrtao gore u "zadatku" je nacrtano CorelDraw-om u minut-dva, tako da možda nisam nacrtao "pravu" sinusoidu, ali zamislite da jest i da su maksimumi jednaki ispod i iznad x-osi - što na slici možda nije. (Nisam mislio da ćete to uočiti.) Shocked
[/quote]
Ono što sam želio reći nije bilo vezano za sliku. Hoću reći da krivulja koju tražiš (paralelna sa siunsoidom, svaka točka ima najmanju udaljenost od sinusoide konstantnu) uopće nije sinusoida, što se vidi iz njene jednadžbe.
[quote]PS. Jesu li derivacije ove dvije funkcije za bilo koji x0 i x1 uvijek jednake?[/quote]
Nisu, ali uz gornje oznake, pošto želiš paralelne krivulje, to je zapravo zahtjev da tangente u A i A' budu paralelne, odnosno B i B' ili u bilo koje druge dvije, na taj način odabrane, točke.
| goranm (napisa): | | Gdje je to zadano? Ako bi udaljenost između točaka na normali bila konstantna, tada dobiveni graf ne bi bio graf funkcije, tj. postojala bi barem jedna točka x koju y2 šalje u dvije vrijednosti. |
Gore iz računa se vidi da se ta situacija dešava samo kada zahtjevamo da je udaljenost veća od 1. Ako je manja od jedan tada se radi o sasvim pravilno zadanoj funkciji (imamo ograničenje da tražena funkcija mora biti ispod grafa sinusoide).
| Citat: | | Prvo moram pomno proučiti tvoj post i malo eksperimentirati, pa tek onda odgovoriti iako me malo bode u oči ovaj korijen u nazivniku (automatski nema rješenje u nekoj točki). |
Vrijednost pod korijenom je uvijek veća ili jednaka jedan, tak da je to definirano u svim točkama (automatski je i cijeli nazivnik veći ili jednak jedan).
| Citat: | | Niti y1 ne izgleda kao sinusoida, udaljenost maksimuma do x-osi je manja od udaljenosti minimuma do x-osi. |
| Citat: | Ovo što sam nacrtao gore u "zadatku" je nacrtano CorelDraw-om u minut-dva, tako da možda nisam nacrtao "pravu" sinusoidu, ali zamislite da jest i da su maksimumi jednaki ispod i iznad x-osi - što na slici možda nije. (Nisam mislio da ćete to uočiti.) Shocked
|
Ono što sam želio reći nije bilo vezano za sliku. Hoću reći da krivulja koju tražiš (paralelna sa siunsoidom, svaka točka ima najmanju udaljenost od sinusoide konstantnu) uopće nije sinusoida, što se vidi iz njene jednadžbe.
| Citat: | | PS. Jesu li derivacije ove dvije funkcije za bilo koji x0 i x1 uvijek jednake? |
Nisu, ali uz gornje oznake, pošto želiš paralelne krivulje, to je zapravo zahtjev da tangente u A i A' budu paralelne, odnosno B i B' ili u bilo koje druge dvije, na taj način odabrane, točke.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 14:13 ned, 11. 5. 2008 Naslov: Postano: 14:13 ned, 11. 5. 2008 Naslov: |
    |
|
|
Evo, nacrto sam u mathematici ovo što sam gore računo. Udaljenost je 0.5. I da, nije baš najbolji naziv dokumenta, trebalo bi pisat krivulja paralelna sa sinusoidom (još jednom, tražena krivulja nije sinusoida)
Evo, dodo sam još jedan crtež, ova žućkasta krivulja predstavlja sinusoidu pomaknutu za konstantu, vidi se da ona ne zadovoljava uvjet sa konstantnom udaljenosti.
Evo, nacrto sam u mathematici ovo što sam gore računo. Udaljenost je 0.5. I da, nije baš najbolji naziv dokumenta, trebalo bi pisat krivulja paralelna sa sinusoidom (još jednom, tražena krivulja nije sinusoida)
Evo, dodo sam još jedan crtež, ova žućkasta krivulja predstavlja sinusoidu pomaknutu za konstantu, vidi se da ona ne zadovoljava uvjet sa konstantnom udaljenosti.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
| Description: |
|

Download |
| Filename: |
dvije sinusoide i krivulja.pdf |
| Filesize: |
43.47 KB |
| Downloaded: |
167 Time(s) |
| Description: |
|

Download |
| Filename: |
paralelne sinusoide.pdf |
| Filesize: |
41.69 KB |
| Downloaded: |
166 Time(s) |
|
|
| [Vrh] |
|
gloryt
Forumaš(ica)

Pridružen/a: 08. 03. 2008. (11:30:40)
Postovi: (B)16
|
 Postano: 13:53 pon, 12. 5. 2008 Naslov: Postano: 13:53 pon, 12. 5. 2008 Naslov: |
    |
|
|
Hvala Alen!
Pokušao sam se malo igrati s tim, onako za po doma. Jasno mi je da si našao pravac koji je okomica na tangentu sinusoide u određenoj točci, a potom si Pitagoru primjenio da dobiješ razmak (d) između te dvije krivulje (sinusoide i ove ... :idea: ... "deformirane sinusoide"). U tom dijelu priče mi nije jasno kako si došao do jednadžbe okomice (normale), a da se nisi uopće zamarao sa tangentom u toj točci?
Ja sam pokušao eksperimentirati počevši od ax+b=y ili sa ax-b=y (nadam se da je to bio dobar početak) i izvlačiti kako da dobijem okomicu, ali uvijek završim s nekim ludim rješenjem. :oops: Možeš li mi molim te kad uloviš vremena napisati postupak kako da dođem do tvoje jednadžbe okomice, jer ja već tu padam? Nije hitno, kad uloviš minut-dva. Sorry na gnjavaži.
Hvala Alen!
Pokušao sam se malo igrati s tim, onako za po doma. Jasno mi je da si našao pravac koji je okomica na tangentu sinusoide u određenoj točci, a potom si Pitagoru primjenio da dobiješ razmak (d) između te dvije krivulje (sinusoide i ove ...  ... "deformirane sinusoide"). U tom dijelu priče mi nije jasno kako si došao do jednadžbe okomice (normale), a da se nisi uopće zamarao sa tangentom u toj točci? ... "deformirane sinusoide"). U tom dijelu priče mi nije jasno kako si došao do jednadžbe okomice (normale), a da se nisi uopće zamarao sa tangentom u toj točci?
Ja sam pokušao eksperimentirati počevši od ax+b=y ili sa ax-b=y (nadam se da je to bio dobar početak) i izvlačiti kako da dobijem okomicu, ali uvijek završim s nekim ludim rješenjem.  Možeš li mi molim te kad uloviš vremena napisati postupak kako da dođem do tvoje jednadžbe okomice, jer ja već tu padam? Nije hitno, kad uloviš minut-dva. Sorry na gnjavaži. Možeš li mi molim te kad uloviš vremena napisati postupak kako da dođem do tvoje jednadžbe okomice, jer ja već tu padam? Nije hitno, kad uloviš minut-dva. Sorry na gnjavaži.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 16:20 pon, 12. 5. 2008 Naslov: Postano: 16:20 pon, 12. 5. 2008 Naslov: |
    |
|
|
Nema problema, za jednadžbu okomice treba nam koeficijent smjera i jedna točka kojom ona prolazi, točka je ona na sinusoidi [latex]\left( {x_0 ,\sin x_0 } \right)[/latex], a za koeficijent smjera prvo uzmemo koeficijent smjera tangente u toj točki, to je [latex]\left( {\sin x_0 } \right)^\prime = \cos x_0 [/latex], a onda koeficijent smjera [latex]k[/latex] pravca koji je okomit na tu tangentu je [latex]k\cos x_0 = - 1 \Rightarrow k = \frac{{ - 1}}
{{\cos x_0 }}[/latex]. Sada je jednadžba okomice [latex]y - \sin x_0 = \frac{{ - 1}}
{{\cos x_0 }}\left( {x - x_0 } \right)[/latex], a de se ne bismo morali mučiti gdje je to definirano, napišemo je u obliku [latex] - \left( {y - \sin x_0 } \right)\cos x_0 = x - x_0[/latex]
Nema problema, za jednadžbu okomice treba nam koeficijent smjera i jedna točka kojom ona prolazi, točka je ona na sinusoidi 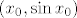 , a za koeficijent smjera prvo uzmemo koeficijent smjera tangente u toj točki, to je , a za koeficijent smjera prvo uzmemo koeficijent smjera tangente u toj točki, to je 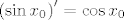 , a onda koeficijent smjera , a onda koeficijent smjera  pravca koji je okomit na tu tangentu je pravca koji je okomit na tu tangentu je 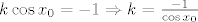 . Sada je jednadžba okomice . Sada je jednadžba okomice 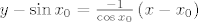 , a de se ne bismo morali mučiti gdje je to definirano, napišemo je u obliku , a de se ne bismo morali mučiti gdje je to definirano, napišemo je u obliku 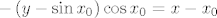
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
gloryt
Forumaš(ica)

Pridružen/a: 08. 03. 2008. (11:30:40)
Postovi: (B)16
|
|
| [Vrh] |
|
|






