Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Derivacije (zadatak)

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Ostalo - ozbiljno -> Čistilište
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Ammex
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2009. (08:18:28)
Postovi: (22)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 18:09 ned, 6. 9. 2009    Naslov: Derivacije Citirajte i odgovorite
y=2x/√(x^2-x)

Može li mi neko pokazat na ovom zadatku kako se računaju derivacije.
Hvala
y=2x/√(x^2-x)

Može li mi neko pokazat na ovom zadatku kako se računaju derivacije.
Hvala


[Vrh]
Korisnički profil Pošaljite privatnu poruku
matmih
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: muško
Sarma = la pohva - posuda
36 = 51 - 15
Lokacija: {Zg, De , Ri}
PostPostano: 19:51 ned, 6. 9. 2009    Naslov: Citirajte i odgovorite
[latex] \displaystyle y=\frac{2x}{\sqrt{x^2-x}} [/latex]

[latex] \displaystyle y'=\frac{(2x)' \cdot \sqrt{x^2-x} - 2x\cdot (\sqrt{x^2-x})'}{(\sqrt{x^2-x})^2}= \frac{2\cdot \sqrt{x^2-x}-2x\cdot \frac{(2x-1)}{2\sqrt{x^2-x}}}{x^2-x} [/latex]
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Ammex
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2009. (08:18:28)
Postovi: (22)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 20:17 ned, 6. 9. 2009    Naslov: Citirajte i odgovorite
le li treba ispat -x/(x^2-x)^1.5
le li treba ispat -x/(x^2-x)^1.5


[Vrh]
Korisnički profil Pošaljite privatnu poruku
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 20:23 ned, 6. 9. 2009    Naslov: Citirajte i odgovorite
Da, no [url=http://www.wolframalpha.com/input/?i=(2x%2F√(x^2-x))']to mozes i sam provjeriti[/url] (v. alternate form). 8)
Da, no to mozes i sam provjeriti (v. alternate form). Cool



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Ammex
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2009. (08:18:28)
Postovi: (22)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 20:41 ned, 6. 9. 2009    Naslov: Citirajte i odgovorite
Kako bi stavili u formulu da je zadatak ovakav?
Tek sam ovo poce ucit.




y=√(2x+3)/(x+1)
Kako bi stavili u formulu da je zadatak ovakav?
Tek sam ovo poce ucit.




y=√(2x+3)/(x+1)


[Vrh]
Korisnički profil Pošaljite privatnu poruku
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 22:10 ned, 6. 9. 2009    Naslov: Citirajte i odgovorite
Ako pitas za WolframAplha: zapakiras formulu (bez "[tt]y=[/tt]") u zagradu i dodas apostrof, kao i ja s prethodnom formulom. 8) Dakle, [url=http://www.wolframalpha.com/input/?i=(√(2x%2B3)%2F(x%2B1))']ovako[/url] (ako se korijen odnosi samo na brojnik). :)

Ako pitas kako se derivira, primijeni [url=http://www.wolframalpha.com/input/?i=(f(x)%2Fg(x))']pravilo za deriviranje razlomka (tj. dijeljenja)[/url], [url=http://www.wolframalpha.com/input/?i=(√f(x))']korijena[/url] i [url=http://www.wolframalpha.com/input/?i=(f(g(x)))']kompozicije[/url] (treba ti za "korijen iz f(x)"):

[latex]y = \frac{\sqrt{f(x)}}{g(x)}[/latex] :arrow:
[latex]y' = \left(\frac{\sqrt{f(x)}}{g(x)}\right)' = \frac{\left(\sqrt{f(x)}\right)' g(x) - \sqrt{f(x)}g'(x)}{g(x)^2} = \frac{\frac{f'(x)}{2\sqrt{f(x)}} g(x) - \sqrt{f(x)}g'(x)}{g(x)^2}[/latex]
Naravno, kod mene su
[latex]f(x) = 2x+3, \quad g(x) = x+1[/latex].
Osnovne derivacije su trivijalne:
[latex]f'(x) = 2, \quad g'(x) = 1[/latex],
a ostalo dobijes uvrstavanje (ako nisam negdje (pr)omashio). 8)
Ako pitas za WolframAplha: zapakiras formulu (bez "y=") u zagradu i dodas apostrof, kao i ja s prethodnom formulom. Cool Dakle, ovako (ako se korijen odnosi samo na brojnik). Smile

Ako pitas kako se derivira, primijeni pravilo za deriviranje razlomka (tj. dijeljenja), korijena i kompozicije (treba ti za "korijen iz f(x)"):

Arrow

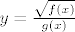
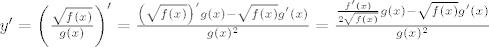
Naravno, kod mene su
.
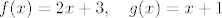Osnovne derivacije su trivijalne:
,
a ostalo dobijes uvrstavanje (ako nisam negdje (pr)omashio). Cool



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Ammex
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2009. (08:18:28)
Postovi: (22)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 9:44 pon, 7. 9. 2009    Naslov: Citirajte i odgovorite
Moze li i formula i iz ovog zadatka kad je korijem u nazivniku?
y=2x/√(x^2-x)
Hvala jos jednom
Moze li i formula i iz ovog zadatka kad je korijem u nazivniku?
y=2x/√(x^2-x)
Hvala jos jednom


[Vrh]
Korisnički profil Pošaljite privatnu poruku
allllice
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 16. 09. 2005. (14:31:59)
Postovi: (121)16
Spol: žensko
Sarma = la pohva - posuda
24 = 28 - 4
Lokacija: Zagreb
PostPostano: 11:17 pon, 7. 9. 2009    Naslov: Citirajte i odgovorite
[quote="matmih"][latex] \displaystyle y'=\frac{(2x)' \cdot \sqrt{x^2-x} - 2x\cdot (\sqrt{x^2-x})'}{(\sqrt{x^2-x})^2}= \frac{2\cdot \sqrt{x^2-x}-2x\cdot \frac{(2x-1)}{2\sqrt{x^2-x}}}{x^2-x} [/latex][/quote]

Tu ti je matmih lijepo sve napisao. To sto je u nazivniku korijen nema nikakve veze, i dalje se primjenjuje ista formula.


Znaci razlomak [latex] \frac{b}{n}[/latex] (gdje je b brojnik, a n nazivnik, i to mogu bili bilo kakve funkcije) deriviras ovako:

[latex] {(\frac{b}{n})}'=\frac{b'*n-b*n'}{n^2}[/latex]

Korijen [latex] \sqrt{x^2-x}[/latex] se derivira ovako:

[latex] (\sqrt{x^2-x})'=[(x^2-x)^{\frac{1}{2}}]'=\frac{1}{2}(x^2-x)^{\frac{1}{2}-1}*(x^2-x)'=\frac{1}{2}(x^2-x)^{-\frac{1}{2}}*(2x-1)=\frac{2x-1}{2\sqrt{x^2-x}}[/latex]
matmih (napisa):


Tu ti je matmih lijepo sve napisao. To sto je u nazivniku korijen nema nikakve veze, i dalje se primjenjuje ista formula.


Znaci razlomak (gdje je b brojnik, a n nazivnik, i to mogu bili bilo kakve funkcije) deriviras ovako:



Korijen se derivira ovako:



[Vrh]
Korisnički profil Pošaljite privatnu poruku
Ammex
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2009. (08:18:28)
Postovi: (22)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 19:55 pon, 7. 9. 2009    Naslov: Citirajte i odgovorite
Može te li mi još samo objasnit kako se dobije max ili min tj.kako se zna da je max ili min?
Može te li mi još samo objasnit kako se dobije max ili min tj.kako se zna da je max ili min?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 21:30 pon, 7. 9. 2009    Naslov: Citirajte i odgovorite
[quote="Ammex"]Može te li mi još samo objasnit kako se dobije max ili min tj.kako se zna da je max ili min?[/quote]

Očito se radi o extremima neke funkcije.

Da bi neka točka ( nazovimo je c ) bila kandidat za extrem, onda mora biti f'(c)=0 (i obratno)
Kad smo našli kandidate za (lokalne) extreme fje f, onda imamo 3 slučaja:
1. f''(c)=0 , to je onda točka inflexije
2. f''(c)<0, to je onda (lokalni) MAXIMUM
3. f''(c)>0, to je onda (lokalni) MINIMUM.

primjer:
[latex]f(x)=x^2+2x+4[/latex]

tražimo kandidate za extreme, tj nultočke derivacije:
[latex] 0 = (x^2+2x+4)' = 2x+2 [/latex]

iz čega slijedi da je ona naša točka c=-1.

Sad se pitamo je li to minimum ili maximum ili točka inflexije, pa gledamo drugu derivaciju:
[latex]f''(x)=2[/latex]

specijalno je f''(-1)=2>0 pa je točka c=-1 lokalni (u ovom slučaju i globalni) minimum.
Ammex (napisa):
Može te li mi još samo objasnit kako se dobije max ili min tj.kako se zna da je max ili min?


Očito se radi o extremima neke funkcije.

Da bi neka točka ( nazovimo je c ) bila kandidat za extrem, onda mora biti f'(c)=0 (i obratno)
Kad smo našli kandidate za (lokalne) extreme fje f, onda imamo 3 slučaja:
1. f''(c)=0 , to je onda točka inflexije
2. f''(c)<0, to je onda (lokalni) MAXIMUM
3. f''(c)>0, to je onda (lokalni) MINIMUM.

primjer:


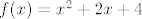
tražimo kandidate za extreme, tj nultočke derivacije:


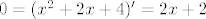
iz čega slijedi da je ona naša točka c=-1.

Sad se pitamo je li to minimum ili maximum ili točka inflexije, pa gledamo drugu derivaciju:


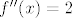
specijalno je f''(-1)=2>0 pa je točka c=-1 lokalni (u ovom slučaju i globalni) minimum.



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
zkoprek
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 09. 2009. (22:56:55)
Postovi: (2)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 2:13 uto, 15. 9. 2009    Naslov: Citirajte i odgovorite
ima netko da bi htio objasnit ovo, koje pravilo je koristi kod deriviranja, jeli konstanta puta nešto, ili je pravilo razlike?


[url=http://www.wolframalpha.com/input/?i=((100*(3Q%2B2007)/(√3Q%2B2007))']Wolfram Alpha derivacija funkcije[/url]
ima netko da bi htio objasnit ovo, koje pravilo je koristi kod deriviranja, jeli konstanta puta nešto, ili je pravilo razlike?


Wolfram Alpha derivacija funkcije


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Gino
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Sarma = la pohva - posuda
-29 = 108 - 137
Lokacija: Pula
PostPostano: 8:16 uto, 15. 9. 2009    Naslov: Citirajte i odgovorite
ides ljepo na [tt]Show steps[/tt] i sve ti pise
ides ljepo na Show steps i sve ti pise



_________________
Mario Berljafa
[Vrh]
Korisnički profil Pošaljite privatnu poruku
zkoprek
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 09. 2009. (22:56:55)
Postovi: (2)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 13:07 uto, 15. 9. 2009    Naslov: Citirajte i odgovorite
[quote="Gino"]ides ljepo na [tt]Show steps[/tt] i sve ti pise[/quote]

hvala, išao sam već, ali chain rule...ja sam na višoj na FOI, i pokušavam skužit kako rješit zadatak za prijatelja, makar sam ja položio...nije da žicam, ali predavanja su prošla pa mi nije friško, a i chain rule se opće ne sjećam da smo spominjali
Gino (napisa):
ides ljepo na Show steps i sve ti pise


hvala, išao sam već, ali chain rule...ja sam na višoj na FOI, i pokušavam skužit kako rješit zadatak za prijatelja, makar sam ja položio...nije da žicam, ali predavanja su prošla pa mi nije friško, a i chain rule se opće ne sjećam da smo spominjali


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Ostalo - ozbiljno -> Čistilište Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan