| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:04 sri, 6. 2. 2008 Naslov: Postano: 19:04 sri, 6. 2. 2008 Naslov: |
    |
|
|
Zašto si integrirao?
Rastav na parcijalne razlomke je [latex]\frac{1}{2n}-\frac{1}{1+n}+\frac{1}{2(2+n)}[/latex]
i sada se kada se malo raspiše imamo
[latex]\frac{1}{2n}-\frac{1}{1+n}+\frac{1}{2(2+n)} + \\
\frac{1}{2(1+n)}-\frac{1}{2+n}+\frac{1}{2(3+n)} + \\
\frac{1}{2(2+n)}-\frac{1}{3+n}+\frac{1}{2(4+n)} +\dots \\
[/latex]
(po mogućnosti točno jedno ispod drugog) i sada ako gledaš članove dijagonalno, od gore desno, prema dolje lijevo, prežive 1/2n, -1/(1+n),1/(2(1+n)), a svi ostali se ponište. Npr.
[latex]\frac{1}{2(k+n)}-\frac{1}{k+n}+\frac{1}{2(k+n)}=\\
\frac{1}{2}\left(\frac{1}{k+n}+\frac{1}{k+n}\right)-\frac{1}{k+n}=0[/latex]
Sada, kako su preživjeli samo [latex]\frac{1}{2n}-\frac{1}{n+1}+\frac{1}{2(n+1)}[/latex], tj. preživjeli su samo za n=1, pa je suma jednaka [latex]\frac{1}{2}-\frac{1}{2}+\frac{1}{2\cdot 2}=\frac{1}{4}[/latex].
Prestigo me..glupi latex :twisted: :lol: :lol:
Zašto si integrirao?
Rastav na parcijalne razlomke je 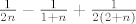
i sada se kada se malo raspiše imamo
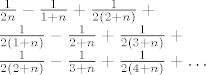
(po mogućnosti točno jedno ispod drugog) i sada ako gledaš članove dijagonalno, od gore desno, prema dolje lijevo, prežive 1/2n, -1/(1+n),1/(2(1+n)), a svi ostali se ponište. Npr.
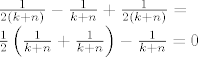
Sada, kako su preživjeli samo 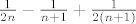 , tj. preživjeli su samo za n=1, pa je suma jednaka , tj. preživjeli su samo za n=1, pa je suma jednaka  . .
Prestigo me..glupi latex   
_________________
The Dude Abides
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 14:38 čet, 7. 2. 2008 Naslov: Postano: 14:38 čet, 7. 2. 2008 Naslov: |
    |
|
|
[quote="napraviculom"]ne mora
niz parcijalnih suma S_n konvergentan --> red je konvergentan -->
s = lim_n S_n je suma reda
EDIT:
[latex]S_n=\displaystyle \sum_{k=1}^{n}\frac{1}{k(k+1)(k+2)}[/latex]
princip je isti, sad se gledaju i gornje granice, nastima se od k=3 do n-2 za 1/k[/quote]
Moram priznati da ne razumijem argument zašto "ne mora". Upravo si sam napisao, ako je niz parcijalnih suma reda konvergentan onda je red konvergentan onda je s=lim_n S_n suma reda. Znači da bi iskoristio da je s=lim_n S_n suma reda, moraš pokazati da niz parcijalnih suma konvergira, tj. da je red konvergentan. Vidim da si napisao "dobije se lim_n [1/4 + 1/2n - 1/(2n-2) ]", ali to samo za sebe, bez konteksta, ništa ne znači [size=9](a vjerojatno je i moj nespretno ubačen post između tvoja dva pridonio tome :oops: )[/size]. Trebao bi dodati da je niz parcijalnih suma konvergentan jer lim_n S_n = lim_n [1/4 + 1/2n - 1/(2n-2) ]=1/4, pa je onda i red konvergentan, pa je s=1/4 :wink:
btw. nije potrebno naštimavanje :)
[latex]\displaystyle\sum_{k=1}^{n}(\frac{1}{2k}-\frac{1}{1+k}+\frac{1}{2(2+k)})=\\
\begin{array}{ccc}
\frac{1}{2} & -\frac{1}{2} & +\frac{1}{6}\\
+\frac{1}{4}&- \frac{1}{3} & +\frac{1}{8}\\
+\frac{1}{6}&- \frac{1}{4} & +\frac{1}{10}\\
\vdots & \vdots & \vdots \\
+\frac{1}{2(n-2)}&- \frac{1}{-1+n} & +\frac{1}{2n}\\
+\frac{1}{2(n-1)}&- \frac{1}{n} & +\frac{1}{2(1+n)}\\
+\frac{1}{2n}&- \frac{1}{1+n} & +\frac{1}{2(2+n)}\\
\end{array}
[/latex]
Sada se, počevši od prve 1/6, po dijagonali svi poništavaju osim
[latex]\frac{1}{2}-\frac{1}{2}+\frac{1}{4}+\frac{1}{2(n+1)}-\frac{1}{1+n}+\frac{1}{2(2+n)}[/latex] :)
| napraviculom (napisa): | ne mora
niz parcijalnih suma S_n konvergentan → red je konvergentan →
s = lim_n S_n je suma reda
EDIT:
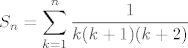
princip je isti, sad se gledaju i gornje granice, nastima se od k=3 do n-2 za 1/k |
Moram priznati da ne razumijem argument zašto "ne mora". Upravo si sam napisao, ako je niz parcijalnih suma reda konvergentan onda je red konvergentan onda je s=lim_n S_n suma reda. Znači da bi iskoristio da je s=lim_n S_n suma reda, moraš pokazati da niz parcijalnih suma konvergira, tj. da je red konvergentan. Vidim da si napisao "dobije se lim_n [1/4 + 1/2n - 1/(2n-2) ]", ali to samo za sebe, bez konteksta, ništa ne znači (a vjerojatno je i moj nespretno ubačen post između tvoja dva pridonio tome  ). Trebao bi dodati da je niz parcijalnih suma konvergentan jer lim_n S_n = lim_n [1/4 + 1/2n - 1/(2n-2) ]=1/4, pa je onda i red konvergentan, pa je s=1/4 ). Trebao bi dodati da je niz parcijalnih suma konvergentan jer lim_n S_n = lim_n [1/4 + 1/2n - 1/(2n-2) ]=1/4, pa je onda i red konvergentan, pa je s=1/4 
btw. nije potrebno naštimavanje 
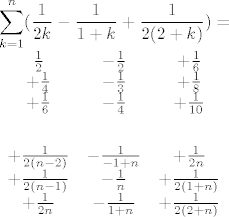
Sada se, počevši od prve 1/6, po dijagonali svi poništavaju osim
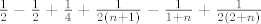 
_________________
The Dude Abides
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 14:52 čet, 7. 2. 2008 Naslov: Re: zadatak 8.4 Postano: 14:52 čet, 7. 2. 2008 Naslov: Re: zadatak 8.4 |
    |
|
|
[quote="ma"][quote="Mr.Doe"][latex]I=1+2+4+8+\dots,~2I=2+4+8+\dots~~,2I+1=I\Rightarrow I=-1[/latex][/quote]
ovo ful ima smisla. :roll:[/quote]
Pa, definitivno je na razini ovoga:
[quote="Luuka"]a ako ln dodefiniramo [b]po neprekidnosti[/b], da je ln(0)=0 onda npr. dobivam da je [latex]\sum_{n=1}^{+\infty}\frac{1}{n+1}=-1[/latex]
[/quote], pa ako je Luuka mogao "natjerati" harmonijski red da konvergira ( i to ka negativnom broju ), zasto ne bi moj red mogao konvergirati. I dalje nisam vidio da je netko rekao u cemu je problem kod mojeg reda.
Takoder, ne razumijem kakav je to simbolicki (?) zapis o kojem Luuka govori.
Mislim da je na ovom topicu napisano puno gluposti, tako da je ovo zadnji post od mene.
Htio bih pohvaliti Gorana na strpljivosti i volji za objasnjavanjem!! :karma:
| ma (napisa): | | Mr.Doe (napisa): | 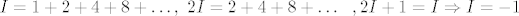 |
ovo ful ima smisla.  |
Pa, definitivno je na razini ovoga:
| Luuka (napisa): | a ako ln dodefiniramo po neprekidnosti, da je ln(0)=0 onda npr. dobivam da je 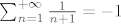
|
, pa ako je Luuka mogao "natjerati" harmonijski red da konvergira ( i to ka negativnom broju ), zasto ne bi moj red mogao konvergirati. I dalje nisam vidio da je netko rekao u cemu je problem kod mojeg reda.
Takoder, ne razumijem kakav je to simbolicki (?) zapis o kojem Luuka govori.
Mislim da je na ovom topicu napisano puno gluposti, tako da je ovo zadnji post od mene.
Htio bih pohvaliti Gorana na strpljivosti i volji za objasnjavanjem!! 
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
|






















