| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
 Postano: 16:57 ned, 9. 3. 2008 Naslov: Postano: 16:57 ned, 9. 3. 2008 Naslov: |
    |
|
|
Čini mi se da nije rekao zašto, rekao je nešto u stilu "mi tu sada možemo petljati sa limesima, ali nećemo, ovako je elegantnije" i onda je uveo onu omega funkciju.
mogu li te pitati gdje se u ovom dokazu koristi činjenica da je f derivabilna? I zašto ne piše derivabilna u c, povlači neprekidna u c? Smije li se odmah ovako generalizirati neprekidnostt i derivabilnost na cijelu funkciju?
I mogu li te zamoliti da staviš i taj dokaz za kompoziciju, ovi mi se tvoji čine jako lijepi, Guljaševi su nemogući....
Čini mi se da nije rekao zašto, rekao je nešto u stilu "mi tu sada možemo petljati sa limesima, ali nećemo, ovako je elegantnije" i onda je uveo onu omega funkciju.
mogu li te pitati gdje se u ovom dokazu koristi činjenica da je f derivabilna? I zašto ne piše derivabilna u c, povlači neprekidna u c? Smije li se odmah ovako generalizirati neprekidnostt i derivabilnost na cijelu funkciju?
I mogu li te zamoliti da staviš i taj dokaz za kompoziciju, ovi mi se tvoji čine jako lijepi, Guljaševi su nemogući....
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
 Postano: 18:21 ned, 9. 3. 2008 Naslov: Postano: 18:21 ned, 9. 3. 2008 Naslov: |
    |
|
|
generalizacija vrijedi. derivabilnost je na nastavi definirana samo u točki, ali derivabilnost u točki povlači neprekidnost u točki. derivabilnost u svakoj točki domene povlači neprekidnost u svakoj točki domene (ako je domena otvoren skup, kako će reći dotični teorem), a neprekidnost [b]u svakoj točki[/b] domene znači neprekidnost [b]na cijeloj domeni[/b]. (ovo je podebljano jer je neprekidnost [b]na otvorenu skupu (intervalu)[/b] posebno definirana kao neprekidnost u svim točkama tog skupa - usporedbe radi, nije definirano što je to derivabilnost na skupu/intervalu... samo u točki)
derivabilnost u c je u onom gore dokazu korištena da se pokaže postojanje limesa funkcije f u točki c. jer ako postoje limesi funkcija [latex]\frac{f(x)-f(c)}{x-c}[/latex] i [latex](x-c)[/latex] kada x teži u c, onda postoji i limes umnoška tih funkcija (po tm.3.2. o operacijama s limesima). taj limes je po iznosu jednak umnošku zasebnih limesa. isto vrijedi i za limes zbroja čime je ona jednakost limesa opravdana. (sjećam se da je ovo sve i guljaš pričao, tako da ne baljezgam.hhahaha)
a dokaz za kompoziciju... samo opet moraš strogo paziti da dobro argumentiraš zašto vrijede jednakosti, zašto će svaki limes u svakom koraku postojati...
[latex]\lim_{x\to c}\frac{(g\circ f)(x)-(g\circ f)(c)}{x-c}=\lim_{x\to c}\left\{\frac{g[f(x)]-g[f(c)]}{x-c}\cdot\frac{f(x)-f(c)}{f(x)-f(c)}\right\}=\lim_{x\to c}\left\{\frac{g[f(x)]-g[f(c)]}{f(x)-f(c)}\cdot\frac{f(x)-f(c)}{x-c}\right\}=\lim_{x\to c}\frac{g[f(x)]-g[f(c)]}{f(x)-f(c)}\cdot\lim_{x\to c}\frac{f(x)-f(c)}{x-c}=\lim_{y\to d}\frac{g(y)-g(d)}{y-d}\cdot\lim_{x\to c}\frac{f(x)-f(c)}{x-c}=g'(d)\cdot f'(c)[/latex]
zamjena f(x) s y u limesima opravdana je time što je f neprekidna u točki c. a zamjena f(c) s d je čisto simbolična
nadam se da sam od pomoći.hehe
generalizacija vrijedi. derivabilnost je na nastavi definirana samo u točki, ali derivabilnost u točki povlači neprekidnost u točki. derivabilnost u svakoj točki domene povlači neprekidnost u svakoj točki domene (ako je domena otvoren skup, kako će reći dotični teorem), a neprekidnost u svakoj točki domene znači neprekidnost na cijeloj domeni. (ovo je podebljano jer je neprekidnost na otvorenu skupu (intervalu) posebno definirana kao neprekidnost u svim točkama tog skupa - usporedbe radi, nije definirano što je to derivabilnost na skupu/intervalu... samo u točki)
derivabilnost u c je u onom gore dokazu korištena da se pokaže postojanje limesa funkcije f u točki c. jer ako postoje limesi funkcija 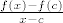 i i  kada x teži u c, onda postoji i limes umnoška tih funkcija (po tm.3.2. o operacijama s limesima). taj limes je po iznosu jednak umnošku zasebnih limesa. isto vrijedi i za limes zbroja čime je ona jednakost limesa opravdana. (sjećam se da je ovo sve i guljaš pričao, tako da ne baljezgam.hhahaha) kada x teži u c, onda postoji i limes umnoška tih funkcija (po tm.3.2. o operacijama s limesima). taj limes je po iznosu jednak umnošku zasebnih limesa. isto vrijedi i za limes zbroja čime je ona jednakost limesa opravdana. (sjećam se da je ovo sve i guljaš pričao, tako da ne baljezgam.hhahaha)
a dokaz za kompoziciju... samo opet moraš strogo paziti da dobro argumentiraš zašto vrijede jednakosti, zašto će svaki limes u svakom koraku postojati...
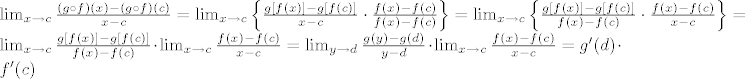
zamjena f(x) s y u limesima opravdana je time što je f neprekidna u točki c. a zamjena f(c) s d je čisto simbolična
nadam se da sam od pomoći.hehe
|
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
 Postano: 18:47 ned, 9. 3. 2008 Naslov: Postano: 18:47 ned, 9. 3. 2008 Naslov: |
    |
|
|
Itekako si od pomoći! Mislim da mi je jasno, ako se predomislim, opet ću se javiti....
A da, odgovor na tvoje drugo pitanje.
mislim da možeš koristiti te dokaze, ali, sjećaš se kada je onaj dečko odgovarao na satu, pa da je pokušao na drugi način, pa ga je prof. stalno zaustavljao, provjeravao, sumnjao, naravno to mu na kraju nije uzeo za zlo (niti treba), ali nisam vidjela da je poslije itko pokušao nešto slično. I vjerujem da postoji razlog zašto nas uči baš tako, pa ako možeš, nauči njegove dokaze, a ovi će ti sigurno pomoći da ih bolje shvatiš!
Ili još bolje, prezentiraš ovako, jer stvarno ne vidim zašto ne, pa ako prof. bude inzistirao ili bude sumnjičav, napraviš I na njegov način. Kapacitet si, možeš ti naučiti I jedan I drugi način, pa zašto ne?!
Itekako si od pomoći! Mislim da mi je jasno, ako se predomislim, opet ću se javiti....
A da, odgovor na tvoje drugo pitanje.
mislim da možeš koristiti te dokaze, ali, sjećaš se kada je onaj dečko odgovarao na satu, pa da je pokušao na drugi način, pa ga je prof. stalno zaustavljao, provjeravao, sumnjao, naravno to mu na kraju nije uzeo za zlo (niti treba), ali nisam vidjela da je poslije itko pokušao nešto slično. I vjerujem da postoji razlog zašto nas uči baš tako, pa ako možeš, nauči njegove dokaze, a ovi će ti sigurno pomoći da ih bolje shvatiš!
Ili još bolje, prezentiraš ovako, jer stvarno ne vidim zašto ne, pa ako prof. bude inzistirao ili bude sumnjičav, napraviš I na njegov način. Kapacitet si, možeš ti naučiti I jedan I drugi način, pa zašto ne?!
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 8:17 pon, 14. 4. 2008 Naslov: Postano: 8:17 pon, 14. 4. 2008 Naslov: |
    |
|
|
[quote="Novi"]Naime javlja se problem sto izraz u nazivniku prvog razlomka u rastavu f(x)-f(c) moze bit nula na recimo citavom nekom intervalu koji sadrzi tocku c, pa takva fja uopce nije definirana u okolini tocke c i nema smisla govorit o njenom limesu u tocki c. [/quote]
Po ovome što si napisao ne mora bit da fja nije definirana oko c... f(x)=C (konstanta) je recimo fja za koju je f(x)-f(c)=0 a ona je neprekidna i derivabilna, svi limesi postoje itd... A i u definicijama se uzimaju intervali i točke na kojima je f definirana...
[quote="Novi"]
Ali sad me vise zanima ovaj prvi dokaz koji iz derivabilnosti vuce neprekidnost, a u kojem nevidim nikakvih mana.......[/quote]
A koji to?
| Novi (napisa): | | Naime javlja se problem sto izraz u nazivniku prvog razlomka u rastavu f(x)-f(c) moze bit nula na recimo citavom nekom intervalu koji sadrzi tocku c, pa takva fja uopce nije definirana u okolini tocke c i nema smisla govorit o njenom limesu u tocki c. |
Po ovome što si napisao ne mora bit da fja nije definirana oko c... f(x)=C (konstanta) je recimo fja za koju je f(x)-f(c)=0 a ona je neprekidna i derivabilna, svi limesi postoje itd... A i u definicijama se uzimaju intervali i točke na kojima je f definirana...
| Novi (napisa): |
Ali sad me vise zanima ovaj prvi dokaz koji iz derivabilnosti vuce neprekidnost, a u kojem nevidim nikakvih mana....... |
A koji to?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:53 pon, 14. 4. 2008 Naslov: Postano: 18:53 pon, 14. 4. 2008 Naslov: |
    |
|
|
ma napadaš i lijevu i desnu...na lijevoj je f(x), kad napadneš s limesom imaš lim(x->c)f(x) a to ne znaš dal postoji da bi se jednakost mogla nastavit...ko da recimo dijeliš s nečim, a ne znaš dal to je 0 ili ne...recimo...
To mi se čini jedinom manom u ovom svemu...nek me netko ispravi ako griješim...
ma napadaš i lijevu i desnu...na lijevoj je f(x), kad napadneš s limesom imaš lim(x->c)f(x) a to ne znaš dal postoji da bi se jednakost mogla nastavit...ko da recimo dijeliš s nečim, a ne znaš dal to je 0 ili ne...recimo...
To mi se čini jedinom manom u ovom svemu...nek me netko ispravi ako griješim...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
 Postano: 19:27 pon, 14. 4. 2008 Naslov: Postano: 19:27 pon, 14. 4. 2008 Naslov: |
    |
|
|
ma valja napadat limesom obje strane. jer, ono što je s desne strane potpuno je jednako onom s lijeve. dakle, ako limes desne strane postoji, postoji sigurno i limes lijeve strane koja je samo drukčiji zapis onoga s desne strane. dakle, poanta je zapisati izraz s lijeve strane, [latex]f(x)[/latex], kao nešto drugo (ali ekvivalentno, uz manja odstupanja koja za napadanje limesom nisu bitna - kao [latex]x\not=c[/latex]), primjerice izraz s desne strane, čiji limes možemo sa sigurnošću reći da postoji i, po potrebi, odrediti njegovu vrijednost.
ma valja napadat limesom obje strane. jer, ono što je s desne strane potpuno je jednako onom s lijeve. dakle, ako limes desne strane postoji, postoji sigurno i limes lijeve strane koja je samo drukčiji zapis onoga s desne strane. dakle, poanta je zapisati izraz s lijeve strane, 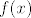 , kao nešto drugo (ali ekvivalentno, uz manja odstupanja koja za napadanje limesom nisu bitna - kao , kao nešto drugo (ali ekvivalentno, uz manja odstupanja koja za napadanje limesom nisu bitna - kao 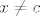 ), primjerice izraz s desne strane, čiji limes možemo sa sigurnošću reći da postoji i, po potrebi, odrediti njegovu vrijednost. ), primjerice izraz s desne strane, čiji limes možemo sa sigurnošću reći da postoji i, po potrebi, odrediti njegovu vrijednost.
Zadnja promjena: PopStevo; 18:26 uto, 15. 4. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 17:05 uto, 15. 4. 2008 Naslov: Postano: 17:05 uto, 15. 4. 2008 Naslov: |
    |
|
|
[quote]ma valja napadat limesom obje strane. jer, ono što je s desne strane potpuno je jednako onom s lijeve. dakle, ako limes desne strane postoji, postoji sigurno i limes lijeve strane koja je samo drukčiji zapis onoga s lijeve strane. dakle, poanta je zapisati izraz s lijeve strane, , kao nešto drugo (ali ekvivalentno, uz manja odstupanja koja za napadanje limesom nisu bitna - kao ), primjerice izraz s desne strane, čiji limes možemo sa sigurnošću reći da postoji i, po potrebi, odrediti njegovu vrijednost.[/quote]
Agree :D
| Citat: | | ma valja napadat limesom obje strane. jer, ono što je s desne strane potpuno je jednako onom s lijeve. dakle, ako limes desne strane postoji, postoji sigurno i limes lijeve strane koja je samo drukčiji zapis onoga s lijeve strane. dakle, poanta je zapisati izraz s lijeve strane, , kao nešto drugo (ali ekvivalentno, uz manja odstupanja koja za napadanje limesom nisu bitna - kao ), primjerice izraz s desne strane, čiji limes možemo sa sigurnošću reći da postoji i, po potrebi, odrediti njegovu vrijednost. |
Agree 
|
|
| [Vrh] |
|
|


















