| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Boris Davidovič
Forumaš(ica)
Pridružen/a: 08. 01. 2004. (23:05:18)
Postovi: (3C)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Boris Davidovič
Forumaš(ica)
Pridružen/a: 08. 01. 2004. (23:05:18)
Postovi: (3C)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Boris Davidovič
Forumaš(ica)
Pridružen/a: 08. 01. 2004. (23:05:18)
Postovi: (3C)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 12:10 pet, 26. 8. 2005 Naslov: Postano: 12:10 pet, 26. 8. 2005 Naslov: |
    |
|
|
[quote="Boris Davidovič"]a) Dokazati da \lijepo(A) nije gust u L(V).[/quote]
det:L(V)->C je neprekidna funkcija.
det(T^-1 A T)=det(A)=:a (označimo taj broj s a)
Zato je \lijepo(A) podskup od det^-1({a}) (praslika skupa {a}), što je zatvoreni skup u L(V), a nije jednak cijelom L(V) jer postoje i operatori s determinantom različitom od a. (Podrazumijeva se da V nije trivijalan.)
Radi toga je i zatvarač od \lijepo(A) podskup od det^-1({a}) pa ne može biti jednak cijelom L(V).
Naime, definicija gustoće skupa S u L(V) (ili općenitijem metričkom/topološkom prostoru) je zatvarač(S)=L(V).
Ono s normom je jedna od karakterizacija, također često korisna.
[quote="Boris Davidovič"]b) Je li \lijepo(A) uvijek zatvoren u L(V)?[/quote]
Nije. Evo protuprimjera za V=C^2. (Operatori su zadani matricama u kanonskoj bazi.)
[code:1]A=[0 1] B_n=[n 0 ]-1 [0 1] [n 0 ] =[0 1/n^2]
[0 0] [0 1/n] [0 0] [0 1/n] [0 0 ][/code:1]
(B_n) je niz u \lijepo(A) i konvergira prema nul-operatoru, koji nije iz \lijepo(A). (Jedino nul-operator je sličan nul-operatoru.)
Dakle, \lijepo(A) u ovom slučaju nije zatvoreni podskup L(V).
| Boris Davidovič (napisa): | | a) Dokazati da \lijepo(A) nije gust u L(V). |
det:L(V)→C je neprekidna funkcija.
det(T^-1 A T)=det(A)=:a (označimo taj broj s a)
Zato je \lijepo(A) podskup od det^-1({a}) (praslika skupa {a}), što je zatvoreni skup u L(V), a nije jednak cijelom L(V) jer postoje i operatori s determinantom različitom od a. (Podrazumijeva se da V nije trivijalan.)
Radi toga je i zatvarač od \lijepo(A) podskup od det^-1({a}) pa ne može biti jednak cijelom L(V).
Naime, definicija gustoće skupa S u L(V) (ili općenitijem metričkom/topološkom prostoru) je zatvarač(S)=L(V).
Ono s normom je jedna od karakterizacija, također često korisna.
| Boris Davidovič (napisa): | | b) Je li \lijepo(A) uvijek zatvoren u L(V)? |
Nije. Evo protuprimjera za V=C^2. (Operatori su zadani matricama u kanonskoj bazi.)
| Kod: | A=[0 1] B_n=[n 0 ]-1 [0 1] [n 0 ] =[0 1/n^2]
[0 0] [0 1/n] [0 0] [0 1/n] [0 0 ] |
(B_n) je niz u \lijepo(A) i konvergira prema nul-operatoru, koji nije iz \lijepo(A). (Jedino nul-operator je sličan nul-operatoru.)
Dakle, \lijepo(A) u ovom slučaju nije zatvoreni podskup L(V).
|
|
| [Vrh] |
|
Boris Davidovič
Forumaš(ica)
Pridružen/a: 08. 01. 2004. (23:05:18)
Postovi: (3C)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 12:23 sub, 27. 8. 2005 Naslov: Postano: 12:23 sub, 27. 8. 2005 Naslov: |
    |
|
|
[quote="Boris Davidovič"]1. Neka je (a_n) niz u hilbertovom prostoru H. Tada je ekvivalentno :
(1) Za sve m iz N a_m nije u Cl([{a_n : n iz N, n!=m}])
(2) Postoji niz (b_n) u H t.d za sve m,n iz N vrijedi (a_m|b_n)= 1 za m=n i 0 za m!=n.[/quote]
(1)=>(2)
L_m=Cl([{a_n : n!=m}]) je zatvoreni potprostor od H.
Svaki a_m možemo napisati kao
a_m=c_m+d_m, gdje je c_m iz L_m, a d_m iz ort.komp. od L_m.
Primijetimo da je d_m različito od [b]0[/b] zbog uvjeta (1) jer bi inače bilo a_m=c_m iz L_m, a to nije.
Definirajmo
[latex]b_m=\frac{d_m}{\|d_m\|^2}[/latex]
Sada se provjeri da je taj niz (b_n) dobar.
(2)=>(1)
[latex]f_m\colon H\to\mathbf{K},\ f_{m}(x):=(x|b_m)[/latex]
je neprekidni linearni funkcional pa mu je jezgra Ker(f_m) zatvoreni potprostor od H.
Zbog uvjeta (2) je a_n iz Ker(f_m) pa je i (zatvarač potprostora generiranog tim vektorima a_n) cijeli L_m podskup od Ker(f_m).
Opet iz uvjeta (2) je f_m(a_m)=1 pa a_m nije u Ker(f_m).
Zaključujemo da a_m nije u L_m.
:changes:
| Boris Davidovič (napisa): | 1. Neka je (a_n) niz u hilbertovom prostoru H. Tada je ekvivalentno :
(1) Za sve m iz N a_m nije u Cl([{a_n : n iz N, n!=m}])
(2) Postoji niz (b_n) u H t.d za sve m,n iz N vrijedi (a_m|b_n)= 1 za m=n i 0 za m!=n. |
(1)⇒(2)
L_m=Cl([{a_n : n!=m}]) je zatvoreni potprostor od H.
Svaki a_m možemo napisati kao
a_m=c_m+d_m, gdje je c_m iz L_m, a d_m iz ort.komp. od L_m.
Primijetimo da je d_m različito od 0 zbog uvjeta (1) jer bi inače bilo a_m=c_m iz L_m, a to nije.
Definirajmo
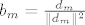
Sada se provjeri da je taj niz (b_n) dobar.
(2)⇒(1)
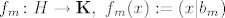
je neprekidni linearni funkcional pa mu je jezgra Ker(f_m) zatvoreni potprostor od H.
Zbog uvjeta (2) je a_n iz Ker(f_m) pa je i (zatvarač potprostora generiranog tim vektorima a_n) cijeli L_m podskup od Ker(f_m).
Opet iz uvjeta (2) je f_m(a_m)=1 pa a_m nije u Ker(f_m).
Zaključujemo da a_m nije u L_m.

|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 12:42 sub, 27. 8. 2005 Naslov: Postano: 12:42 sub, 27. 8. 2005 Naslov: |
    |
|
|
[quote="Boris Davidovič"]2. V KDVP nad R i A iz L(V), te p(x) iz R[x] polinom bez realnih nultočaka s vodećim koeficijentom 1. Tada je det(p(A))>=0.[/quote]
Svaki polinom p(x) iz R[x] se može jednoznačno rastaviti na ireducibilne faktore, tj. kao vodeći koef. (koji je ionako 1) puta produkt konačno mnogo polinoma oblika x-c (c€R) i oblika x^2+ax+b (a,b€R, a^2-4b<0).
Faktora oblika x-c naš polinom nema jer nema realnih nultočaka.
Zato je p(x) produkt kvadratnih polinoma oblika x^2+ax+b, tj. p(A) je produkt operatora oblika A^2+aA+bI, a,b€R, a^2-4b<0. Po Binet-Cauchyjevom teoremu je det(p(A)) produkt determinanti det(A^2+aA+bI) pa je dovoljno dokazati da je svaka od njih >=0.
Dakle, dokazujemo jednostavniju tvrdnju: det(A^2+aA+bI)>=0 za a,b€R, a^2-4b<0.
Nadopunimo kvadratni polinom do potpunog kvadrata:
[latex]\det(A^2+aA+bI)=\det\left((A+\frac{a}{2}I)^2+\frac{4b-a^2}{4}I\right)=[/latex]
[latex]( \ \textrm{ozna\v{c}imo kra\'{c}e} \ B=A+\frac{a}{2}I, \ c=\sqrt{\frac{4b-a^2}{4}}>0 \ )[/latex]
[latex]=\det(B^2+c^2 I)=\det((B+ciI)(B-ciI))=|\det(B+ciI)|^2 \geq 0[/latex]
| Boris Davidovič (napisa): | | 2. V KDVP nad R i A iz L(V), te p(x) iz R[x] polinom bez realnih nultočaka s vodećim koeficijentom 1. Tada je det(p(A))>=0. |
Svaki polinom p(x) iz R[x] se može jednoznačno rastaviti na ireducibilne faktore, tj. kao vodeći koef. (koji je ionako 1) puta produkt konačno mnogo polinoma oblika x-c (c€R) i oblika x^2+ax+b (a,b€R, a^2-4b<0).
Faktora oblika x-c naš polinom nema jer nema realnih nultočaka.
Zato je p(x) produkt kvadratnih polinoma oblika x^2+ax+b, tj. p(A) je produkt operatora oblika A^2+aA+bI, a,b€R, a^2-4b<0. Po Binet-Cauchyjevom teoremu je det(p(A)) produkt determinanti det(A^2+aA+bI) pa je dovoljno dokazati da je svaka od njih >=0.
Dakle, dokazujemo jednostavniju tvrdnju: det(A^2+aA+bI)>=0 za a,b€R, a^2-4b<0.
Nadopunimo kvadratni polinom do potpunog kvadrata:
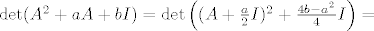
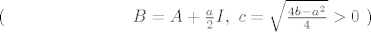
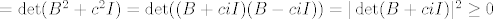
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
kyra29
Forumaš(ica)

Pridružen/a: 16. 02. 2009. (17:23:47)
Postovi: (3F)16
Spol: 
|
|
| [Vrh] |
|
**dreamer**
Forumaš(ica)

Pridružen/a: 27. 06. 2008. (15:25:24)
Postovi: (2F)16
Lokacija: space
|
 Postano: 13:25 uto, 2. 2. 2010 Naslov: Postano: 13:25 uto, 2. 2. 2010 Naslov: |
    |
|
|
evo ja cu pokusati...
minimalni polinom je jednak (x^100-1)^2=(x^50-1)(x^50+1)
iz toga slijedi x^50 je element od {-1,1}, odnosno x je element od {-i,i,-1,1} (jer se radi o kompleksnom prostoru), a to je upravo spektar od A
sin(aA^50+b) je nilpotentan akko mu je spektar jednak 0
<==> (po teoremu o preslikavanju spektra) sin(a*spektar(A)^50+b)=0
<==> sin(-a+b)=0 i sin(a+b)=0 <==> -a+b=k*pi, a+b=l*pi, k,l cijeli brojevi.
na kraju dobijes a=(k+l)*pi/2, b=(l-k)*pi/2
nadam se da se moze skuziti iz ovog rijesenje :) ako nije jasno pitaj
evo ja cu pokusati...
minimalni polinom je jednak (x^100-1)^2=(x^50-1)(x^50+1)
iz toga slijedi x^50 je element od {-1,1}, odnosno x je element od {-i,i,-1,1} (jer se radi o kompleksnom prostoru), a to je upravo spektar od A
sin(aA^50+b) je nilpotentan akko mu je spektar jednak 0
<==> (po teoremu o preslikavanju spektra) sin(a*spektar(A)^50+b)=0
<==> sin(-a+b)=0 i sin(a+b)=0 <==> -a+b=k*pi, a+b=l*pi, k,l cijeli brojevi.
na kraju dobijes a=(k+l)*pi/2, b=(l-k)*pi/2
nadam se da se moze skuziti iz ovog rijesenje  ako nije jasno pitaj ako nije jasno pitaj
_________________
You may say that I’m dreamer but I’m not the only one
|
|
| [Vrh] |
|
kyra29
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (17:23:47)
Postovi: (3F)16
Spol: 
|
|
| [Vrh] |
|
**dreamer**
Forumaš(ica)

Pridružen/a: 27. 06. 2008. (15:25:24)
Postovi: (2F)16
Lokacija: space
|
 Postano: 14:05 uto, 2. 2. 2010 Naslov: Postano: 14:05 uto, 2. 2. 2010 Naslov: |
    |
|
|
vidi.. nisam ni skuzila da ima i druga grupa :D
ti si vjerojatno dobila da ti je spektar od A jednak {-1,1}, al spektar ti je {-i,i,-1,1} jer se radi o kompleksnom prostoru pa moras rastaviti na sve nultocke minimalnog polinoma, i realne i kompleksne.
Te nultocke dobijes na sljedeci nacin : (x^200-1)^2=(x^200-1)(x^200-1), a x^200-1=(x^100-1)(x^100-1)=(x^50-1)(x^50+1)(x^50-i)(x^50+i)=...
i kad bi tako do kraja rastavljala dobila bi da su ti nultocke -1,1,-i,i (odnosno da je to spektar od A).
Nadam se da je sad jasnije.
vidi.. nisam ni skuzila da ima i druga grupa 
ti si vjerojatno dobila da ti je spektar od A jednak {-1,1}, al spektar ti je {-i,i,-1,1} jer se radi o kompleksnom prostoru pa moras rastaviti na sve nultocke minimalnog polinoma, i realne i kompleksne.
Te nultocke dobijes na sljedeci nacin : (x^200-1)^2=(x^200-1)(x^200-1), a x^200-1=(x^100-1)(x^100-1)=(x^50-1)(x^50+1)(x^50-i)(x^50+i)=...
i kad bi tako do kraja rastavljala dobila bi da su ti nultocke -1,1,-i,i (odnosno da je to spektar od A).
Nadam se da je sad jasnije.
_________________
You may say that I’m dreamer but I’m not the only one
|
|
| [Vrh] |
|
kyra29
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (17:23:47)
Postovi: (3F)16
Spol: 
|
 Postano: 14:14 uto, 2. 2. 2010 Naslov: Postano: 14:14 uto, 2. 2. 2010 Naslov: |
    |
|
|
meni nastane problem kad taj spektar, znači (1,-1,i,-i) uvrstavam u cos(aA^100+b), koju god svojstvenu vrijednost uvrstila dobijem isto...
meni nastane problem kad taj spektar, znači (1,-1,i,-i) uvrstavam u cos(aA^100+b), koju god svojstvenu vrijednost uvrstila dobijem isto...
|
|
| [Vrh] |
|
**dreamer**
Forumaš(ica)

Pridružen/a: 27. 06. 2008. (15:25:24)
Postovi: (2F)16
Lokacija: space
|
|
| [Vrh] |
|
kyra29
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (17:23:47)
Postovi: (3F)16
Spol: 
|
|
| [Vrh] |
|
**dreamer**
Forumaš(ica)

Pridružen/a: 27. 06. 2008. (15:25:24)
Postovi: (2F)16
Lokacija: space
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
 Postano: 14:58 uto, 2. 2. 2010 Naslov: Postano: 14:58 uto, 2. 2. 2010 Naslov: |
    |
|
|
[quote="**dreamer**"]evo ja cu pokusati...
minimalni polinom je jednak (x^100-1)^2=(x^50-1)(x^50+1)
iz toga slijedi x^50 je element od {-1,1}, odnosno x je element od {-i,i,-1,1} (jer se radi o kompleksnom prostoru), a to je upravo spektar [/quote]
Ti stvarno mislis da su jedine nultocke od x^100=1 iz skupa {1,-1,i,-i} ?
:wacky:
Valjda si tek na prvoj godini :P
kyra, nisi smjela "popusiti" takvu glupost :P, ipak ces uskoro biti bakalar :)
sto se rjesenja tice...naime, znas da je x^200=1, znaci x^100 je 1 ili -1...po teoremu o spektru znas da mora vrijediti sin(alpha*(lambda)^100+beta)=0
ali znas da je lambda^100=1 ili -1
uvrsti ta dva uvjeta gore, i dobit ces uvjete na alphu i betu ;)
EDIT: nisam skuzio da je kolegica bila brza
| **dreamer** (napisa): | evo ja cu pokusati...
minimalni polinom je jednak (x^100-1)^2=(x^50-1)(x^50+1)
iz toga slijedi x^50 je element od {-1,1}, odnosno x je element od {-i,i,-1,1} (jer se radi o kompleksnom prostoru), a to je upravo spektar |
Ti stvarno mislis da su jedine nultocke od x^100=1 iz skupa {1,-1,i,-i} ?

Valjda si tek na prvoj godini 
kyra, nisi smjela "popusiti" takvu glupost  , ipak ces uskoro biti bakalar , ipak ces uskoro biti bakalar 
sto se rjesenja tice...naime, znas da je x^200=1, znaci x^100 je 1 ili -1...po teoremu o spektru znas da mora vrijediti sin(alpha*(lambda)^100+beta)=0
ali znas da je lambda^100=1 ili -1
uvrsti ta dva uvjeta gore, i dobit ces uvjete na alphu i betu 
EDIT: nisam skuzio da je kolegica bila brza
|
|
| [Vrh] |
|
|
















