| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Kolan
Forumaš(ica)

Pridružen/a: 28. 01. 2010. (10:31:36)
Postovi: (1)16
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
 Postano: 11:56 čet, 28. 1. 2010 Naslov: Postano: 11:56 čet, 28. 1. 2010 Naslov: |
    |
|
|
uvrsti ove [latex]\sigma_1[/latex] i [latex]\sigma_2[/latex] u zadnju jednadzbu,nades nultocke polinoma i to su ti kandidati za [latex]\sigma_3[/latex]...jedino ce ti [latex]\sigma_3=-3[/latex] kad uvrstis u [latex]\sigma_1[/latex] i [latex]\sigma_2[/latex] proc uvjet zadatka...
sad imas tri jednadzbe:
[latex]x+y+z=-1[/latex]
[latex]xy+yz+xz=-5[/latex]
[latex]xyz=-3[/latex]
kako su ti to ujedno i vietove formule za polinom 3. stupnja,imas da su ti [latex]x,y,z[/latex] nultocke pripadajuceg polinoma [latex]t^3+t^2-5t+3[/latex],odnosno [latex]1,1,-3[/latex] i sve permutacije...
uvrsti ove 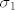 i i 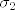 u zadnju jednadzbu,nades nultocke polinoma i to su ti kandidati za u zadnju jednadzbu,nades nultocke polinoma i to su ti kandidati za 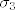 ...jedino ce ti ...jedino ce ti 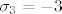 kad uvrstis u kad uvrstis u 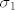 i i 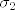 proc uvjet zadatka... proc uvjet zadatka...
sad imas tri jednadzbe:
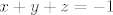
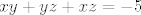
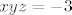
kako su ti to ujedno i vietove formule za polinom 3. stupnja,imas da su ti 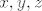 nultocke pripadajuceg polinoma nultocke pripadajuceg polinoma 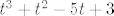 ,odnosno ,odnosno 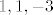 i sve permutacije... i sve permutacije...
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
 Postano: 12:28 čet, 28. 1. 2010 Naslov: Postano: 12:28 čet, 28. 1. 2010 Naslov: |
    |
|
|
znaci:
baza:provjeris za 1,kako to vridi ides na pretpostavku
pretpostavka:pretpostavimo da tvrdnja vrijedi tralalala...
i korak(u kojem dokazijes da vrijedi za n+1):
[latex]1*1+2*3+...+n(2n-1)+(n+1)(2n+1)=\frac{1}{6}(n+1)(n+2)(4n+3)[/latex]
iskoristis pretpostavku,pa imas:
[latex]\frac{1}{6}n(n+1)(4n-1)+(n+1)(2n+1)=\frac{1}{6}(n+1)(n+2)(4n+3)[/latex]...
i sad mozes to na nekoliko nacina pokazat...mislim da je nama asistentica govorila da pravi matematicari ovo ne bi jednostavno razmnozili i pokratili i dobili 0=0 (ili nesto slicno),mada to nije netocno...mislim da smo mi kod nje ovu lijevu stranu nastimavali da bude jednaka desnoj,mada ni to nije problem...ti uradi po savjesti,mislim da dalje ne bi trebalo bit problema,al ako zapnes,javi...
znaci:
baza:provjeris za 1,kako to vridi ides na pretpostavku
pretpostavka:pretpostavimo da tvrdnja vrijedi tralalala...
i korak(u kojem dokazijes da vrijedi za n+1):
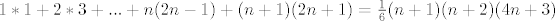
iskoristis pretpostavku,pa imas:
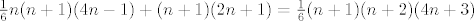 ... ...
i sad mozes to na nekoliko nacina pokazat...mislim da je nama asistentica govorila da pravi matematicari ovo ne bi jednostavno razmnozili i pokratili i dobili 0=0 (ili nesto slicno),mada to nije netocno...mislim da smo mi kod nje ovu lijevu stranu nastimavali da bude jednaka desnoj,mada ni to nije problem...ti uradi po savjesti,mislim da dalje ne bi trebalo bit problema,al ako zapnes,javi...
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
biba1804
Forumaš(ica)

Pridružen/a: 27. 01. 2010. (14:34:03)
Postovi: (3)16
|
 Postano: 13:32 čet, 28. 1. 2010 Naslov: Postano: 13:32 čet, 28. 1. 2010 Naslov: |
    |
|
|
[quote="jkrstic"]uvrsti ove [latex]\sigma_1[/latex] i [latex]\sigma_2[/latex] u zadnju jednadzbu,nades nultocke polinoma i to su ti kandidati za [latex]\sigma_3[/latex]...jedino ce ti [latex]\sigma_3=-3[/latex] kad uvrstis u [latex]\sigma_1[/latex] i [latex]\sigma_2[/latex] proc uvjet zadatka...
sad imas tri jednadzbe:
[latex]x+y+z=-1[/latex]
[latex]xy+yz+xz=-5[/latex]
[latex]xyz=-3[/latex]
kako su ti to ujedno i vietove formule za polinom 3. stupnja,imas da su ti [latex]x,y,z[/latex] nultocke pripadajuceg polinoma [latex]t^3+t^2-5t+3[/latex],odnosno [latex]1,1,-3[/latex] i sve permutacije...[/quote]
odkuda nam nultočke 1.1.3 :oops:
| jkrstic (napisa): | uvrsti ove 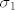 i i 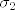 u zadnju jednadzbu,nades nultocke polinoma i to su ti kandidati za u zadnju jednadzbu,nades nultocke polinoma i to su ti kandidati za 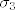 ...jedino ce ti ...jedino ce ti 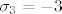 kad uvrstis u kad uvrstis u 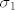 i i 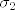 proc uvjet zadatka... proc uvjet zadatka...
sad imas tri jednadzbe:
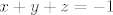
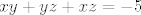
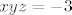
kako su ti to ujedno i vietove formule za polinom 3. stupnja,imas da su ti 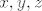 nultocke pripadajuceg polinoma nultocke pripadajuceg polinoma 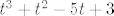 ,odnosno ,odnosno 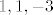 i sve permutacije... i sve permutacije... |
odkuda nam nultočke 1.1.3 
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 14:09 čet, 28. 1. 2010 Naslov: Postano: 14:09 čet, 28. 1. 2010 Naslov: |
    |
|
|
[quote="niveus"]@Darija.x hvala na informacijama
@biba1804 nultočke su brojevi koji dijele slobodni član znači to su mogućnost +-3, +-1 i sad je jasno da je nultočka 3,1 a pošto je 1 dvostruku nultočku zato imamo 1,1,3
Jel može neko dokazati
5^(n+2)+7^n da je djeljiv sa 12 za sve neparne prirodne brojeve :)[/quote]
baza
5^3 + 7 = 132 = 11*12
pretpostavka
za neki k vrijedi
12| 5^(2k + 3) + 7^(2k + 1)
korak
[latex]5^{2k + 5} + 7^{2k + 3} = 25 \cdot 5^{2k + 3} + 49 \cdot 7^{2k + 1} = 24 \cdot 5^{2k + 3} + 48 \cdot 7^{2k + 1} + (5^{2k + 3} + 7^{2k + 1})[/latex]
Prva dva pribrojnika su djeljiva sa 12, a treci je djeljiv sa 12 po pretpostavci
*bonus* (dokaz koji nije indkucijom ali je elegantniji :)
Lako se vidi da za n neparan broj vrijedi [latex]x^n + y^n = (x + y)(x^{n-1} - x^{n-2}y + x^{n - 3}y^2 - \ldots +x^2y^{n-3} - xy^{n-2} + y^{n - 1}) [/latex]
Sada imamo 5^(n+2) + 7^n = 25 * 5^n + 7^n = 24 * 5^n + (5^n + 7^n)
5^n + 7^n = (5 + 7) * ..., pa je djeljivo s 12, a prvi pribrojnik je takoder djeljiv s 12
| niveus (napisa): | @Darija.x hvala na informacijama
@biba1804 nultočke su brojevi koji dijele slobodni član znači to su mogućnost +-3, +-1 i sad je jasno da je nultočka 3,1 a pošto je 1 dvostruku nultočku zato imamo 1,1,3
Jel može neko dokazati
5^(n+2)+7^n da je djeljiv sa 12 za sve neparne prirodne brojeve  |
baza
5^3 + 7 = 132 = 11*12
pretpostavka
za neki k vrijedi
12| 5^(2k + 3) + 7^(2k + 1)
korak
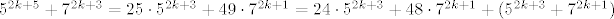
Prva dva pribrojnika su djeljiva sa 12, a treci je djeljiv sa 12 po pretpostavci
*bonus* (dokaz koji nije indkucijom ali je elegantniji 
Lako se vidi da za n neparan broj vrijedi 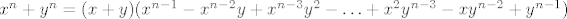
Sada imamo 5^(n+2) + 7^n = 25 * 5^n + 7^n = 24 * 5^n + (5^n + 7^n)
5^n + 7^n = (5 + 7) * ..., pa je djeljivo s 12, a prvi pribrojnik je takoder djeljiv s 12
_________________
Bri
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
 Postano: 14:23 čet, 28. 1. 2010 Naslov: Postano: 14:23 čet, 28. 1. 2010 Naslov: |
    |
|
|
[quote="Grga"][quote="niveus"]@Darija.x hvala na informacijama
@biba1804 nultočke su brojevi koji dijele slobodni član znači to su mogućnost +-3, +-1 i sad je jasno da je nultočka 3,1 a pošto je 1 dvostruku nultočku zato imamo 1,1,3
Jel može neko dokazati
5^(n+2)+7^n da je djeljiv sa 12 za sve neparne prirodne brojeve :)[/quote]
baza
5^3 + 7 = 132 = 11*12
pretpostavka
za neki k vrijedi
12| 5^(2k + 3) + 7^(2k + 1)
korak
[latex]5^{2k + 5} + 7^{2k + 3} = 25 \cdot 5^{2k + 3} + 49 \cdot 7^{2k + 1} = 24 \cdot 5^{2k + 3} + 48 \cdot 7^{2k + 1} + (5^{2k + 3} + 7^{2k + 1})[/latex]
Prva dva pribrojnika su djeljiva sa 12, a treci je djeljiv sa 12 po pretpostavci
*bonus* (dokaz koji nije indkucijom ali je elegantniji :)
Lako se vidi da za n neparan broj vrijedi [latex]x^n + y^n = (x + y)(x^{n-1} - x^{n-2}y + x^{n - 3}y^2 - \ldots +x^2y^{n-3} - xy^{n-2} + y^{n - 1}) [/latex]
Sada imamo 5^(n+2) + 7^n = 25 * 5^n + 7^n = 24 * 5^n + (5^n + 7^n)
5^n + 7^n = (5 + 7) * ..., pa je djeljivo s 12, a prvi pribrojnik je takoder djeljiv s 12[/quote]
pretpostavljam da si ti u svome dokazu zapisiva n kao 2k+1,pa bi tribalo naglasit da je k cijeli broj [latex]\geq0[/latex]...pa baza ide za [latex]k=0[/latex]
| Grga (napisa): | | niveus (napisa): | @Darija.x hvala na informacijama
@biba1804 nultočke su brojevi koji dijele slobodni član znači to su mogućnost +-3, +-1 i sad je jasno da je nultočka 3,1 a pošto je 1 dvostruku nultočku zato imamo 1,1,3
Jel može neko dokazati
5^(n+2)+7^n da je djeljiv sa 12 za sve neparne prirodne brojeve  |
baza
5^3 + 7 = 132 = 11*12
pretpostavka
za neki k vrijedi
12| 5^(2k + 3) + 7^(2k + 1)
korak
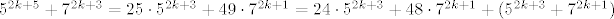
Prva dva pribrojnika su djeljiva sa 12, a treci je djeljiv sa 12 po pretpostavci
*bonus* (dokaz koji nije indkucijom ali je elegantniji 
Lako se vidi da za n neparan broj vrijedi 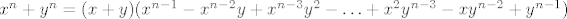
Sada imamo 5^(n+2) + 7^n = 25 * 5^n + 7^n = 24 * 5^n + (5^n + 7^n)
5^n + 7^n = (5 + 7) * ..., pa je djeljivo s 12, a prvi pribrojnik je takoder djeljiv s 12 |
pretpostavljam da si ti u svome dokazu zapisiva n kao 2k+1,pa bi tribalo naglasit da je k cijeli broj 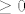 ...pa baza ide za ...pa baza ide za 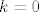
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 16:11 čet, 28. 1. 2010 Naslov: Postano: 16:11 čet, 28. 1. 2010 Naslov: |
    |
|
|
evo ga:
kljuc zadatka je u usporedjivanju stupnjeva:
pretpostavimo da postoji polinom p koji zadovoljava uvjete, neka je st(p)=n
sad gledamo stupanj polinoma s lijeve strane:
st(1+p(x))=n (to je ocito, jer samo si poveco slobodni koeficijent s ovom jedinicom).
st(p')=n-1 (po definiciji derivacije), pa kad komponiras p' i p(x)+1 stupnjevi se mnoze i dobijes da je stupanj polinoma s lijeve strane n*(n-1)
S desne strane je nesto kompliciranija situacija; ako je n neparan, onda ce se vodeci clanovi od ova dva polinoma pokratit (to je najbolje vidjet na primjeru, al jasno je, bit ce suprotnog predznaka)
dakle, u slucaju da je n neparan, desna strana ima stupanj n-1
Buduci da vrijedi jednakost, moraju bit isti stupnjevi, dakle vrijedi
n*(n-1)=n-1 ocito je jedino rjesenje ove jednadzbe n=1, a to se kosi s uvjetom zadatka (koji kaze stupanj polinoma je veci od 1)
Sad prelazimo na drugi slucaj, a taj je kad je n paran
Tad se nece nista precudno dogadjat na desnoj strani, pa ce ukupni stupanj desne strane bit tocno n (zbrajamo dva polinoma stupnja n, ovaj put se nece nista kratit; opet, najbolje je vidjet primjer)
sad opet iz jednakosti stupnjeva imamo n(n-1)=n, a to ima rjesenja 0 i 2
0 odbacujemo, i sad dobivamo da je jedina moguca varijanta st(p)=2
Sad znamo da je p oblika p(x)=ax^2+bx+c pa ga ubacimo u pocetni izraz:
prvo nam treba p'(x)=2ax+b
sad imamo iz pocetnog uvjeta
p'(ax^2+bx+c+1)=p(x+1)+p(1-x), sad raspisemo to i dobijemo:
[latex]2a(ax^2+bx+c+1)+b=a(x+1)^2+b(x+1)+c + a(1-x)^2+b(1-x)+c[/latex]
ovaj izraz se sredi i dobije se neki sustav jednadzbi iz kojeg nadjemo a,b,c (ovaj dio je dost nespretan za pisat tu al zato je i nesto laksi od prvog dijela zadatka):
[latex]2a^2x^2+2abx+2a(c+1)=ax^2+2ax+a+bx+b+c+a-2ax+ax^2+b-bx+c[/latex]
[latex]2a^2x^2+2abx+2a(c+1)=2ax^2+2a+2b+2c[/latex]
sad iz usporedjivanja koefa dobijemo:
2a^2=2a, pa znamo a=1 (a=0 ne moze bit inace imamo prvi stupanj samo)
2ab=0 , pa je b=0
2a(c+1)=2a+2b+2c, tj 2c+2=2+2c, dakle nema uvjeta nad c
iz ovog sad vidimo da je jedino moguce rj. p(x)=x^2+c
u svakom slucaju, sad bi jos trebalo uvrstit taj polinom u pocetni uvjet i vidjet dal je dobro sve...
evo ga:
kljuc zadatka je u usporedjivanju stupnjeva:
pretpostavimo da postoji polinom p koji zadovoljava uvjete, neka je st(p)=n
sad gledamo stupanj polinoma s lijeve strane:
st(1+p(x))=n (to je ocito, jer samo si poveco slobodni koeficijent s ovom jedinicom).
st(p')=n-1 (po definiciji derivacije), pa kad komponiras p' i p(x)+1 stupnjevi se mnoze i dobijes da je stupanj polinoma s lijeve strane n*(n-1)
S desne strane je nesto kompliciranija situacija; ako je n neparan, onda ce se vodeci clanovi od ova dva polinoma pokratit (to je najbolje vidjet na primjeru, al jasno je, bit ce suprotnog predznaka)
dakle, u slucaju da je n neparan, desna strana ima stupanj n-1
Buduci da vrijedi jednakost, moraju bit isti stupnjevi, dakle vrijedi
n*(n-1)=n-1 ocito je jedino rjesenje ove jednadzbe n=1, a to se kosi s uvjetom zadatka (koji kaze stupanj polinoma je veci od 1)
Sad prelazimo na drugi slucaj, a taj je kad je n paran
Tad se nece nista precudno dogadjat na desnoj strani, pa ce ukupni stupanj desne strane bit tocno n (zbrajamo dva polinoma stupnja n, ovaj put se nece nista kratit; opet, najbolje je vidjet primjer)
sad opet iz jednakosti stupnjeva imamo n(n-1)=n, a to ima rjesenja 0 i 2
0 odbacujemo, i sad dobivamo da je jedina moguca varijanta st(p)=2
Sad znamo da je p oblika p(x)=ax^2+bx+c pa ga ubacimo u pocetni izraz:
prvo nam treba p'(x)=2ax+b
sad imamo iz pocetnog uvjeta
p'(ax^2+bx+c+1)=p(x+1)+p(1-x), sad raspisemo to i dobijemo:
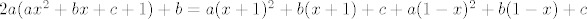
ovaj izraz se sredi i dobije se neki sustav jednadzbi iz kojeg nadjemo a,b,c (ovaj dio je dost nespretan za pisat tu al zato je i nesto laksi od prvog dijela zadatka):
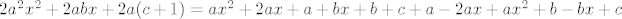
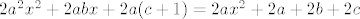
sad iz usporedjivanja koefa dobijemo:
2a^2=2a, pa znamo a=1 (a=0 ne moze bit inace imamo prvi stupanj samo)
2ab=0 , pa je b=0
2a(c+1)=2a+2b+2c, tj 2c+2=2+2c, dakle nema uvjeta nad c
iz ovog sad vidimo da je jedino moguce rj. p(x)=x^2+c
u svakom slucaju, sad bi jos trebalo uvrstit taj polinom u pocetni uvjet i vidjet dal je dobro sve...
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
|














