| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:56 čet, 29. 4. 2010 Naslov: Postano: 21:56 čet, 29. 4. 2010 Naslov: |
    |
|
|
2.9 (a) Tu se više radi o "integralnim produktima", nego o sumama :D. Prirodno se javlja ideja da to čudo logaritmiramo. Dakle, promatrajmo limes [latex]\displaystyle \lim_{n \to +\infty} \frac{1}{n} \sum_{k = 1}^n \left( \frac{k}{n} \right)^2 \ln \left( 1 + \frac{k}{n} \right)[/latex]. Iz aviona je očito da je to jedna Riemann-ova (konkretno, gornja Darboux-ova, nacrtaj si ako pomaže) suma funkcije [latex]x \mapsto x^2 \ln(1+x)[/latex] na segmentu [latex][0,1][/latex] (ovdje je, kao i u skoro svim ostalim zadacima, subdivizija ima [latex]n+1[/latex] ekvidistantnih točaka, te je [latex]\xi_k = \frac{k}{n}[/latex]). To znači da je spomenuti limes jednak [latex]\displaystyle \int \limits_0^1 x^2 \ln(1+x)\,dx[/latex]. Taj integral ne bi trebao biti neki problem izračunati :cijepam: (hint: [color=white]parcijalna integracija sa u=ln(1+x) i dv=x^2 dx[/color]). Dobi se [latex]\frac{2 \ln{2}}{3} - \frac{5}{18}[/latex]. Konačno rješenje je "e na to".
2.9 (a) Tu se više radi o "integralnim produktima", nego o sumama  . Prirodno se javlja ideja da to čudo logaritmiramo. Dakle, promatrajmo limes . Prirodno se javlja ideja da to čudo logaritmiramo. Dakle, promatrajmo limes 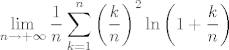 . Iz aviona je očito da je to jedna Riemann-ova (konkretno, gornja Darboux-ova, nacrtaj si ako pomaže) suma funkcije . Iz aviona je očito da je to jedna Riemann-ova (konkretno, gornja Darboux-ova, nacrtaj si ako pomaže) suma funkcije 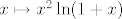 na segmentu na segmentu 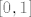 (ovdje je, kao i u skoro svim ostalim zadacima, subdivizija ima (ovdje je, kao i u skoro svim ostalim zadacima, subdivizija ima 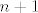 ekvidistantnih točaka, te je ekvidistantnih točaka, te je 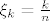 ). To znači da je spomenuti limes jednak ). To znači da je spomenuti limes jednak 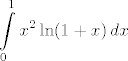 . Taj integral ne bi trebao biti neki problem izračunati . Taj integral ne bi trebao biti neki problem izračunati  (hint: parcijalna integracija sa u=ln(1+x) i dv=x^2 dx). Dobi se (hint: parcijalna integracija sa u=ln(1+x) i dv=x^2 dx). Dobi se 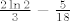 . Konačno rješenje je "e na to". . Konačno rješenje je "e na to".
Zadnja promjena: pmli; 22:22 čet, 29. 4. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 22:05 čet, 29. 4. 2010 Naslov: Postano: 22:05 čet, 29. 4. 2010 Naslov: |
    |
|
|
Kvragu, nisam dobro pročitao pa sam prvo napisao za b)... pa ako budeš trebao i za to, reci :)
A za a), pošto je logaritam neprekidna funkcija, vrijedi da je [latex]\displaystyle {\rm ln} \! \lim_{n \to \infty} \sqrt[n]{\prod_{k=1}^n (1 + \frac kn)^{k^2/n^2}} = \displaystyle \lim_{n \to \infty} {\rm ln} \> \sqrt[n]{\prod_{k=1}^n (1 + \frac kn)^{k^2/n^2}}[/latex], što bi trebalo bitno olakšati stvar ;) Pitaj ako zapne dalje.
Edit: al pmli je naravno bio brži, pa neće trebati :P
Kvragu, nisam dobro pročitao pa sam prvo napisao za b)... pa ako budeš trebao i za to, reci 
A za a), pošto je logaritam neprekidna funkcija, vrijedi da je 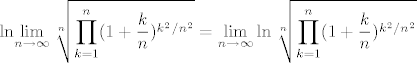 , što bi trebalo bitno olakšati stvar , što bi trebalo bitno olakšati stvar  Pitaj ako zapne dalje. Pitaj ako zapne dalje.
Edit: al pmli je naravno bio brži, pa neće trebati 
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 10:40 pet, 30. 4. 2010 Naslov: Postano: 10:40 pet, 30. 4. 2010 Naslov: |
    |
|
|
Super, hvala, a što se tiče provjere kod 2.9 pod b, jel rješenje kojim slučajem arctg(3)-arctg(2)?
Još jedno pitanje, što se tiče ovog integrala:
[latex] \displaystyle \int \frac{1}{\sqrt{2+x-x^{2}}} \, dx[/latex]
intuitivno mi je jasno rješenje koje izbacuje wolframalpha ( [latex] \displaystyle -arcsin(\frac{1}{3} (1-2x)) [/latex], ali kako ga se dobije računski bez "pogađanja"?
Super, hvala, a što se tiče provjere kod 2.9 pod b, jel rješenje kojim slučajem arctg(3)-arctg(2)?
Još jedno pitanje, što se tiče ovog integrala:
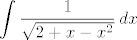
intuitivno mi je jasno rješenje koje izbacuje wolframalpha ( 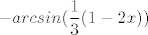 , ali kako ga se dobije računski bez "pogađanja"? , ali kako ga se dobije računski bez "pogađanja"?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
|



















