| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 19:03 ned, 19. 3. 2006 Naslov: 2 zadacica Postano: 19:03 ned, 19. 3. 2006 Naslov: 2 zadacica |
    |
|
|
Imam dva zadacica koja neznam rješiti alko bi mi netko mogao pomoći
1. Provjeriti koje od sljedećih skupova su realni vektorski prostori (uz ustandardna zbrajanja i množenja skalarom) te za one koji to jesu naći jednu bazu i dimenziju:
a)V={0}C_R (C_ znači podskup),
b)V={-1,0,1},
c)V=[-1,1]C_R i
2. Provjeriti koje od sljedećih funkcija su linearni operatori te za one koji to jesu naći sliku i jezgru:
a)f:C^3-> C^2, definirana s f(z1,z2,z3):=z2+2z3 (ovo z2 potez, neznam to napisati)
b)f:C-> R^2, definirana s f(x+iy):=(3x,2x+y,1)
c)f:{(x1,x2,x3)ER^3: x2=x1}->C^2, def. s f(x1,x2,x3):=(x1+ix3,-x2)
d)f:C-> C, definirana s f(z).=|z|
Imam dva zadacica koja neznam rješiti alko bi mi netko mogao pomoći
1. Provjeriti koje od sljedećih skupova su realni vektorski prostori (uz ustandardna zbrajanja i množenja skalarom) te za one koji to jesu naći jednu bazu i dimenziju:
a)V={0}C_R (C_ znači podskup),
b)V={-1,0,1},
c)V=[-1,1]C_R i
2. Provjeriti koje od sljedećih funkcija su linearni operatori te za one koji to jesu naći sliku i jezgru:
a)f:C^3-> C^2, definirana s f(z1,z2,z3):=z2+2z3 (ovo z2 potez, neznam to napisati)
b)f:C-> R^2, definirana s f(x+iy):=(3x,2x+y,1)
c)f:{(x1,x2,x3)ER^3: x2=x1}->C^2, def. s f(x1,x2,x3):=(x1+ix3,-x2)
d)f:C-> C, definirana s f(z).=|z|
|
|
| [Vrh] |
|
vjakovac
Forumaš s poteškoćama u pisanju

Pridružen/a: 28. 02. 2006. (10:07:16)
Postovi: (4B)16
|
 Postano: 21:28 ned, 19. 3. 2006 Naslov: Re: 2 zadacica Postano: 21:28 ned, 19. 3. 2006 Naslov: Re: 2 zadacica |
    |
|
|
[quote="Anonymous"]a)V={0}C_R (C_ znači podskup), [/quote]
{0} jest vektorski prostor, dimenzije 0, baza mu je [latex]\emptyset[/latex].
Kako se provjeri da je to vektorski potprostor od R? Trivijalno:
Za svaka dva skalara a,b€R vrijedi: a*0+b*0=0.
[quote="Anonymous"]b)V={-1,0,1},[/quote]
Nije vektorski prostor jer nije zatvoren na množenje skalarom, npr. 2*1=2, što nije iz {-1,0,1}.
[quote="Anonymous"]c)V=[-1,1]C_R [/quote]
Nije vektorski prostor, isti razlog kao pod (b).
(Ovo je čini se bio zadatak broj 0 iz neke zbirke.)
[quote="Anonymous"]a)f:C^3-> [b]C[/b], definirana s f(z1,z2,z3):=z2+2z3 (ovo z2 potez, neznam to napisati)[/quote]
Nije linearni operator. Npr. f(i,0,0)=-i, i*f(1,0,0)=i*1=i, ali to dvoje bi trebalo biti jednako.
[quote="Anonymous"]b)f:C-> R^[b]3[/b], definirana s f(x+iy):=(3x,2x+y,1)[/quote]
Nije linearni operator npr. zato što je f(0)=(0,0,1), a trebalo bi biti f(0)=(0,0,0).
[quote="Anonymous"]c)f:{(x1,x2,x3)ER^3: x2=x1}->C^2, def. s f(x1,x2,x3):=(x1+ix3,-x2)[/quote]
Ovako kako piše isto nije linearni operator, jer je v.p. s lijeve strane realan, a v.p. s desne strane kompleksan. Linearnost se definira samo za operatore između vektorskih prostora nad istim poljem. Ako pak C^2 shvatimo kao R^4, onda to jest linearni operator.
[quote="Anonymous"]d)f:C-> C, definirana s f(z).=|z|[/quote]
Nije linearni operator. Npr. f(i)=1, i*f(1)=i*1=i, ali to dvoje bi trebalo biti jednako.
| Anonymous (napisa): | | a)V={0}C_R (C_ znači podskup), |
{0} jest vektorski prostor, dimenzije 0, baza mu je  . .
Kako se provjeri da je to vektorski potprostor od R? Trivijalno:
Za svaka dva skalara a,b€R vrijedi: a*0+b*0=0.
| Anonymous (napisa): | | b)V={-1,0,1}, |
Nije vektorski prostor jer nije zatvoren na množenje skalarom, npr. 2*1=2, što nije iz {-1,0,1}.
| Anonymous (napisa): | | c)V=[-1,1]C_R |
Nije vektorski prostor, isti razlog kao pod (b).
(Ovo je čini se bio zadatak broj 0 iz neke zbirke.)
| Anonymous (napisa): | | a)f:C^3→ C, definirana s f(z1,z2,z3):=z2+2z3 (ovo z2 potez, neznam to napisati) |
Nije linearni operator. Npr. f(i,0,0)=-i, i*f(1,0,0)=i*1=i, ali to dvoje bi trebalo biti jednako.
| Anonymous (napisa): | | b)f:C→ R^3, definirana s f(x+iy):=(3x,2x+y,1) |
Nije linearni operator npr. zato što je f(0)=(0,0,1), a trebalo bi biti f(0)=(0,0,0).
| Anonymous (napisa): | | c)f:{(x1,x2,x3)ER^3: x2=x1}→C^2, def. s f(x1,x2,x3):=(x1+ix3,-x2) |
Ovako kako piše isto nije linearni operator, jer je v.p. s lijeve strane realan, a v.p. s desne strane kompleksan. Linearnost se definira samo za operatore između vektorskih prostora nad istim poljem. Ako pak C^2 shvatimo kao R^4, onda to jest linearni operator.
| Anonymous (napisa): | | d)f:C→ C, definirana s f(z).=|z| |
Nije linearni operator. Npr. f(i)=1, i*f(1)=i*1=i, ali to dvoje bi trebalo biti jednako.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 23:04 pet, 24. 3. 2006 Naslov: Postano: 23:04 pet, 24. 3. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Molim vas ako mi možete pojasniti zadatak pod 2. c) ako je linearan operator šta onda da li trebam samo dati neki primjer ili da provjeravam po definiciji aditivnost i homogenost.[/quote]
Opcenito:
Ako nesto [b]nije[/b], onda ti je dovoljan protuprimjer na kojem se vidi da nije (jer "nije" znaci "mozda je istina za [i]neke[/i] ali sigurno nije istina za [i]sve[/i], pa je dosta naci tog jednog za kojeg nije istina). 8)
Ako zelis pokazati da nesto [b]je[/b] (tj. da "vrijedi za sve"), onda moras dokazati da vrijedi za sve. :D Dakle, konkretnu u ovom slucaju za koji pitas, trebas dokazati linearnost (provjerom aditivnosti i homogenosti). :)
| Anonymous (napisa): | | Molim vas ako mi možete pojasniti zadatak pod 2. c) ako je linearan operator šta onda da li trebam samo dati neki primjer ili da provjeravam po definiciji aditivnost i homogenost. |
Opcenito:
Ako nesto nije, onda ti je dovoljan protuprimjer na kojem se vidi da nije (jer "nije" znaci "mozda je istina za neke ali sigurno nije istina za sve, pa je dosta naci tog jednog za kojeg nije istina). 
Ako zelis pokazati da nesto je (tj. da "vrijedi za sve"), onda moras dokazati da vrijedi za sve.  Dakle, konkretnu u ovom slucaju za koji pitas, trebas dokazati linearnost (provjerom aditivnosti i homogenosti). Dakle, konkretnu u ovom slucaju za koji pitas, trebas dokazati linearnost (provjerom aditivnosti i homogenosti). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
vjakovac
Forumaš s poteškoćama u pisanju


Pridružen/a: 28. 02. 2006. (10:07:16)
Postovi: (4B)16
|
 Postano: 0:45 sub, 25. 3. 2006 Naslov: Postano: 0:45 sub, 25. 3. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Molim vas ako mi možete pojasniti zadatak pod 2. c) ako je linearan operator šta onda da li trebam samo dati neki primjer ili da provjeravam po definiciji aditivnost i homogenost.[/quote]
U kontekstu zadatka 2.c) razmisli o ovom što ti je vsego napisao. Zatim se odluči želiš li tvrdnju dokazati ili opovrgnuti. :lol:
Ja sam gore napisao da, doslovno ovako kako piše, f po definiciji nije linearni operator jer mu domena i kodomena nisu vektorski prostori nad istim poljem. To ne znači da se zadatak ne bi mogao malo "popraviti" tako da ima "više" smisla. Ako kodomenu zamijenimo s CxR (prema formuli se čini da je to bila namjera) i onda CxR shvatimo kao RxRxR, tj. realni vektorski prostor dimenzije 3 (naprosto C identificiramo s R^2), zadatak poprima sljedeći oblik:
[color=orange](Ako ti nešto dosad nije bilo jasno, zanemari i čitaj odavde. :) )[/color]
[latex]f\colon\{(x_1,x_2,x_3)\in\mathbb{R}^3 : x_2=x_1\}\to\mathbb{C}\times\mathbb{R}\\ f(x_1,x_2,x_3)=(x_1+i x_3,-x_2)[/latex]
Domenu možemo jednostavnije zapisati pa je zapravo:
[latex]f\colon\{(x_1,x_1,x_3) : x_1,x_3\in\mathbb{R}\}\to\mathbb{C}\times\mathbb{R}\\ f(x_1,x_1,x_3)=(x_1+i x_3,-x_1)[/latex]
Dakle, svuda sam zamijenio x_2 sa x_1.
Da je to linearni operator vidi se iz računa:
[latex]f(\alpha(x_1,x_1,x_3)+\beta(x'_1,x'_1,x'_3))=f(\alpha x_1+\beta x'_1,\alpha x_1+\beta x'_1,\alpha x_3+\beta x'_3)\\=((\alpha x_1+\beta x'_1)+i(\alpha x_3+\beta x'_3),-(\alpha x_1+\beta x'_1))[/latex]
[latex]\alpha f(x_1,x_1,x_3)+\beta f(x'_1,x'_1,x'_3)=\alpha (x_1+i x_3,-x_1)+\beta (x'_1+i x'_3,-x'_1)\\=((\alpha x_1+\beta x'_1)+i(\alpha x_3+\beta x'_3),-(\alpha x_1+\beta x'_1))[/latex]
i to dvoje je jednako.
Slika od f je naprosto:
[latex]\{(x_1+i x_3,-x_1) : x_1,x_3\in\mathbb{R}\}\\
=\{x_1 (1,-1)+ x_3 (i,0) : x_1,x_3\in\mathbb{R}\}[/latex]
i baza joj je {(1,-1),(i,0)}, dimenzija joj je 2.
Jezgra od f je skup svih [latex](x_1,x_1,x_3)[/latex] takvih da je [latex](x_1+i x_3,-x_1)=(0,0)[/latex], tj. [latex]x_1=0, \ x_3=0[/latex]
Tako da je jezgra samo {(0,0,0)}, dimenzija joj je 0.
Mogli smo to zakljuciti i po teoremu o rangu i defektu:
r(f)=2 => d(f)=2-r(f)=0
| Anonymous (napisa): | | Molim vas ako mi možete pojasniti zadatak pod 2. c) ako je linearan operator šta onda da li trebam samo dati neki primjer ili da provjeravam po definiciji aditivnost i homogenost. |
U kontekstu zadatka 2.c) razmisli o ovom što ti je vsego napisao. Zatim se odluči želiš li tvrdnju dokazati ili opovrgnuti. 
Ja sam gore napisao da, doslovno ovako kako piše, f po definiciji nije linearni operator jer mu domena i kodomena nisu vektorski prostori nad istim poljem. To ne znači da se zadatak ne bi mogao malo "popraviti" tako da ima "više" smisla. Ako kodomenu zamijenimo s CxR (prema formuli se čini da je to bila namjera) i onda CxR shvatimo kao RxRxR, tj. realni vektorski prostor dimenzije 3 (naprosto C identificiramo s R^2), zadatak poprima sljedeći oblik:
(Ako ti nešto dosad nije bilo jasno, zanemari i čitaj odavde.  ) )
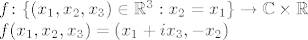
Domenu možemo jednostavnije zapisati pa je zapravo:
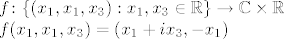
Dakle, svuda sam zamijenio x_2 sa x_1.
Da je to linearni operator vidi se iz računa:
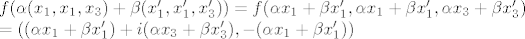
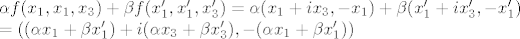
i to dvoje je jednako.
Slika od f je naprosto:
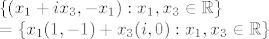
i baza joj je {(1,-1),(i,0)}, dimenzija joj je 2.
Jezgra od f je skup svih 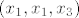 takvih da je takvih da je 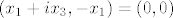 , tj. , tj. 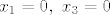
Tako da je jezgra samo {(0,0,0)}, dimenzija joj je 0.
Mogli smo to zakljuciti i po teoremu o rangu i defektu:
r(f)=2 ⇒ d(f)=2-r(f)=0
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|





