| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Markec
Forumaš(ica)

Pridružen/a: 20. 02. 2003. (14:49:45)
Postovi: (134)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Markec
Forumaš(ica)

Pridružen/a: 20. 02. 2003. (14:49:45)
Postovi: (134)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
popravljac
Forumaš(ica)

Pridružen/a: 20. 02. 2009. (14:05:48)
Postovi: (D)16
|
|
| [Vrh] |
|
crna
Forumaš(ica)
Pridružen/a: 20. 11. 2006. (23:03:04)
Postovi: (C)16
|
|
| [Vrh] |
|
sanja86
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (11:19:30)
Postovi: (F)16
Lokacija: nigdjezemska
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:18 čet, 25. 2. 2010 Naslov: Postano: 16:18 čet, 25. 2. 2010 Naslov: |
    |
|
|
[quote="sanja86"]jel mi može ko dati hint za 1. zadatak. nisam sigurna od kud bih počela, a jednostavan je :oops:[/quote]
pod a), smjer [latex]\Rightarrow[/latex]:
Neka vrijedi lijeva strana, te neka je [latex]x \in A[/latex]. Trebam dokazati [latex]x \in B^C[/latex] ili [latex]x \in C[/latex]. Mogu nastupiti 2 slučaja: [latex]x \in B[/latex] ili [latex]x \notin B[/latex]. U prvom slučaju, imamo [latex]x \in A \cap B[/latex], pa je po pretpostavci na lijevoj strani [latex]x \in C[/latex]. Ako [latex]x \notin B[/latex], tada je [latex]x \in B^C[/latex]. Dakle, u oba slučaja je [latex]x \in C \cup B^C[/latex], pa smo dokazali [latex]A \subseteq C \cup B^C[/latex].
Obrat, i pod b) pokušaj sama. Ako nešto nije jasno, pitaj 8)
| sanja86 (napisa): | jel mi može ko dati hint za 1. zadatak. nisam sigurna od kud bih počela, a jednostavan je  |
pod a), smjer  : :
Neka vrijedi lijeva strana, te neka je 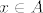 . Trebam dokazati . Trebam dokazati 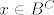 ili ili 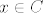 . Mogu nastupiti 2 slučaja: . Mogu nastupiti 2 slučaja: 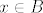 ili ili 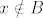 . U prvom slučaju, imamo . U prvom slučaju, imamo 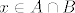 , pa je po pretpostavci na lijevoj strani , pa je po pretpostavci na lijevoj strani 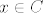 . Ako . Ako 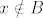 , tada je , tada je 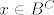 . Dakle, u oba slučaja je . Dakle, u oba slučaja je 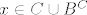 , pa smo dokazali , pa smo dokazali 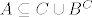 . .
Obrat, i pod b) pokušaj sama. Ako nešto nije jasno, pitaj 
|
|
| [Vrh] |
|
sanja86
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (11:19:30)
Postovi: (F)16
Lokacija: nigdjezemska
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 10:42 pon, 22. 3. 2010 Naslov: Postano: 10:42 pon, 22. 3. 2010 Naslov: |
    |
|
|
[quote="lucika"]može pomoć za zadatak 12 pod a)?
ak uzmem da mi je (x, y) iz R :arrow: (y, x) iz R^-1
jer je R podskup od Q slijedi i da je (y, x) iz Q^-1, ali zašto je R^-1 podskup
od Q^-1 :?: :?[/quote]
(x, y) je iz R^-1
(y, x) je iz R
(y, x) je iz Q (jer je R podskup od Q)
(x, y) je iz Q^-1
| lucika (napisa): | može pomoć za zadatak 12 pod a)?
ak uzmem da mi je (x, y) iz R  (y, x) iz R^-1 (y, x) iz R^-1
jer je R podskup od Q slijedi i da je (y, x) iz Q^-1, ali zašto je R^-1 podskup
od Q^-1   |
(x, y) je iz R^-1
(y, x) je iz R
(y, x) je iz Q (jer je R podskup od Q)
(x, y) je iz Q^-1
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 0:00 čet, 25. 3. 2010 Naslov: Postano: 0:00 čet, 25. 3. 2010 Naslov: |
    |
|
|
[quote="Ančica"]moze pomoc s 5. zadatkom iz proslogodisnjeg kolokvija? hvala![/quote]
Ja imam ideju, ali ne znam koliko je to dobro. :D
Pretpostavimo da Q nije tranzitivna...
Znači da postoje x,y,z td. xQy i yQz ali x neQ z (ovo neQ mi je kao prekriženo Q, tj. (x, z) nisu u relaciji Q)
xQy povlači xRy jer je Q očito podskup od R
yQz povlači yRz is istog razloga
xRy i yRz povlači xRz jer je R tranzitivna
xRz i x neQ z povlači x = z. (Kad bi bilo x različito od z i xRz, onda bi (po definiciji od Q) bilo xQz)
x = z i yRz povlači yRx
xRy i yRx povlači x = y jer je R antisimetrična
xQy i x = y je kontradikcija s definicijom relacije Q.
Dakle, Q je tranzitivna.
Slično za antisimetričnost...
| Ančica (napisa): | | moze pomoc s 5. zadatkom iz proslogodisnjeg kolokvija? hvala! |
Ja imam ideju, ali ne znam koliko je to dobro. 
Pretpostavimo da Q nije tranzitivna...
Znači da postoje x,y,z td. xQy i yQz ali x neQ z (ovo neQ mi je kao prekriženo Q, tj. (x, z) nisu u relaciji Q)
xQy povlači xRy jer je Q očito podskup od R
yQz povlači yRz is istog razloga
xRy i yRz povlači xRz jer je R tranzitivna
xRz i x neQ z povlači x = z. (Kad bi bilo x različito od z i xRz, onda bi (po definiciji od Q) bilo xQz)
x = z i yRz povlači yRx
xRy i yRx povlači x = y jer je R antisimetrična
xQy i x = y je kontradikcija s definicijom relacije Q.
Dakle, Q je tranzitivna.
Slično za antisimetričnost...
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
GCOX
Forumaš(ica)

Pridružen/a: 24. 10. 2006. (12:43:03)
Postovi: (A8)16
Spol: 
Lokacija: SPLIT_ZAGREB
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
|

















