| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
skuharic
Forumaš(ica)

Pridružen/a: 05. 11. 2008. (12:55:48)
Postovi: (C)16
|
|
| [Vrh] |
|
tperkov
Forumaš(ica)
Pridružen/a: 08. 12. 2008. (15:17:18)
Postovi: (71)16
|
 Postano: 0:33 uto, 9. 12. 2008 Naslov: Postano: 0:33 uto, 9. 12. 2008 Naslov: |
    |
|
|
5. A-------------C---------------D--------------B
[latex]
\vec{AC}=\vec{CD}=\vec{DB}\\
\vec{CD}=3\vec{\imath}-2\vec{\jmath}-2\vec{k}=\vec{AC}=\vec{DB}\\
$dakle $
2-x_a=3, -y_a=-2, 2-z_a=-2,$ pa je $A=(-1,2,4)\\
$sli\v{c}no $ B=(8,-4,-2)
[/latex]
1. Treba provjeriti da su AB i CD paralelne stranice, tj. sa su
[latex]\vec{AB} $ i $ \vec{CD}[/latex] kolinearni vektori.
[latex]
\vec{AB}=-2\vec{\imath}+3\vec{\jmath}-3\vec{k}\\
\vec{CD}=4\vec{\imath}-6\vec{\jmath}+6\vec{k}\\
\vec{CD}=-2\vec{AB}[/latex]
Duljine osnovica su duljine tih vektora:
[latex]
|\vec{AB}|=\sqrt{2^2+3^2+3^2}=\sqrt{22}\\
|\vec{CD}|=\sqrt{88}=2\sqrt{22}[/latex]
Kosinuse kuteva računaš pomoću skalarnog produkta, pa kuteve iz kosinusa, to mi se ne da...
2. računanje je dosadno, evo uputa:
a) imaš formulu za ortogonalnu projekciju vektora na ravninu. u tu formulu uvrstiš vektor smjera zadanog pravca. to što izračunaš ti je onda vektor smjera ortogonalne projekcije pravca na ravninu. treba još jedna točka, a to je probodište pravca i ravnine (rješenje sustava jednadžbi pravca i jednadžbe ravnine)
b) sinus kuta između pravca i ravnine je jednak kosinusu kuta između vektora smjera pravca i vektora normale ravnine!
c) a ne znam, možda ima i jednostavnije, al prvo što mi pada na pamet je, kad već imaš pod b) izračunat kut, taj simetrični stoji pod istim kutem prema ravnini, samo na drugoj strani, a probodište je zajednička točka, mislim da je to dovoljno, trenutno nemam volje raspisivati.
5. A-------------C---------------D--------------B
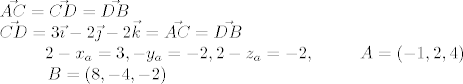
1. Treba provjeriti da su AB i CD paralelne stranice, tj. sa su
 kolinearni vektori. kolinearni vektori.
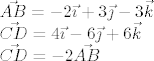
Duljine osnovica su duljine tih vektora:
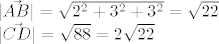
Kosinuse kuteva računaš pomoću skalarnog produkta, pa kuteve iz kosinusa, to mi se ne da...
2. računanje je dosadno, evo uputa:
a) imaš formulu za ortogonalnu projekciju vektora na ravninu. u tu formulu uvrstiš vektor smjera zadanog pravca. to što izračunaš ti je onda vektor smjera ortogonalne projekcije pravca na ravninu. treba još jedna točka, a to je probodište pravca i ravnine (rješenje sustava jednadžbi pravca i jednadžbe ravnine)
b) sinus kuta između pravca i ravnine je jednak kosinusu kuta između vektora smjera pravca i vektora normale ravnine!
c) a ne znam, možda ima i jednostavnije, al prvo što mi pada na pamet je, kad već imaš pod b) izračunat kut, taj simetrični stoji pod istim kutem prema ravnini, samo na drugoj strani, a probodište je zajednička točka, mislim da je to dovoljno, trenutno nemam volje raspisivati.
|
|
| [Vrh] |
|
girl_00
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (21:29:13)
Postovi: (A)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 15:05 sri, 1. 7. 2009 Naslov: Postano: 15:05 sri, 1. 7. 2009 Naslov: |
    |
|
|
evo nekako ovako:
[latex]i^0 = 1[/latex] - svaki broj na nultu je jedan pa je tako i imaginarna jedinica
[latex]i^1 = i[/latex] - svaki broj na prvu je taj isti broj, pa je tako i imaginarna jedinica
[latex]i^2 = -1[/latex] - ovo je naš i po definiciji
dalje računamo :D
[latex]i^3 = i^2 \cdot i= -1 \cdot i = -i[/latex]
[latex]i^4 = (i^2)\cdot (i^2)=(-1)\cdot(-1)=1[/latex]
[latex]i^5 = i^4 \cdot i = i[/latex]
i sad vidiš da ti se ponavlja...
pravilo je ovakvo:
ako je potencija od i djeljiva s 4, onda je rezultat 1
ako potencija daje ostatak 1 pri dijeljenju sa 4, onda je rezultat i
ako potencija daje ostatak 2 pri dijeljenju sa 4, onda je rezultat -1
ako potencija daje ostatak 3 pri dijeljenju sa 4, onda je rezultat -i
Najlakše ti je ostatak gledat ovako:
za djeljivost s 4 su ti bitne samo zadnje dvije znamenke.
dakle, [latex]i^{154978} = i^{78}[/latex]
sada gledaš ostatak toga pri djeljenju s 4, a pošto je 76/4=19
onda je
[latex] i^{78} = i^{76} \cdot i^2 =-1[/latex]
jer je [latex]i^2=-1[/latex]
evo nekako ovako:
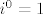 - svaki broj na nultu je jedan pa je tako i imaginarna jedinica - svaki broj na nultu je jedan pa je tako i imaginarna jedinica
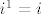 - svaki broj na prvu je taj isti broj, pa je tako i imaginarna jedinica - svaki broj na prvu je taj isti broj, pa je tako i imaginarna jedinica
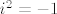 - ovo je naš i po definiciji - ovo je naš i po definiciji
dalje računamo 
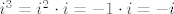
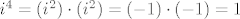
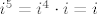
i sad vidiš da ti se ponavlja...
pravilo je ovakvo:
ako je potencija od i djeljiva s 4, onda je rezultat 1
ako potencija daje ostatak 1 pri dijeljenju sa 4, onda je rezultat i
ako potencija daje ostatak 2 pri dijeljenju sa 4, onda je rezultat -1
ako potencija daje ostatak 3 pri dijeljenju sa 4, onda je rezultat -i
Najlakše ti je ostatak gledat ovako:
za djeljivost s 4 su ti bitne samo zadnje dvije znamenke.
dakle, 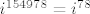
sada gledaš ostatak toga pri djeljenju s 4, a pošto je 76/4=19
onda je
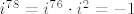
jer je 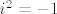
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
girl_00
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (21:29:13)
Postovi: (A)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
girl_00
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (21:29:13)
Postovi: (A)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
girl_00
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (21:29:13)
Postovi: (A)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
girl_00
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (21:29:13)
Postovi: (A)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
|








