| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
Ivanaa
Forumaš(ica)
Pridružen/a: 18. 10. 2010. (22:26:06)
Postovi: (35)16
|
 Postano: 15:40 uto, 28. 12. 2010 Naslov: Postano: 15:40 uto, 28. 12. 2010 Naslov: |
    |
|
|
Buduci da je [latex]f(x)=\log_2x[/latex] strogo rastuca funkcija dovoljno je naci infimum i supremum od [latex]\frac{10mn}{(2m+5n)^2}[/latex] pa ce onda [latex]log_2[/latex] od toga biti infimum i supremum od S.
Ocito je [latex]\frac{10mn}{(2m+5n)^2}>0[/latex] buduci da su m i n prirodni brojevi, a ako uzmemo da je [latex]n=1, m\to \infty, \displaystyle\lim_{m\to \infty}\frac{10m}{(2m+5)^2}=0[/latex]. Dakle infimum od S ne postoji.
Za supremum moramo dobiti neku gornju medu ovog izraza odnosno od cega je [latex]\frac{10mn}{(2m+5n)^2}=\frac{10mn}{4m^2+20mn+25n^2}[/latex] manje ili jednako. Buduci da je [latex]\frac{4m^2+25n^2}{2}\geq \sqrt{4m^2\cdot 25n^2} \Longrightarrow \frac{10mn}{4m^2+20mn+25n^2}\leq \frac{1}{4}[/latex], a za [latex]m=5, n=2 \frac{10mn}{(2m+5n)^2}=\frac{1}{4}[/latex]. Dakle supremum od S je [latex]\log_2 \frac{1}{4}=-2[/latex]
To je valjda to, ak si htio samo hint ispricavam se.
Buduci da je 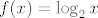 strogo rastuca funkcija dovoljno je naci infimum i supremum od strogo rastuca funkcija dovoljno je naci infimum i supremum od 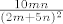 pa ce onda pa ce onda 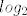 od toga biti infimum i supremum od S. od toga biti infimum i supremum od S.
Ocito je 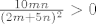 buduci da su m i n prirodni brojevi, a ako uzmemo da je buduci da su m i n prirodni brojevi, a ako uzmemo da je 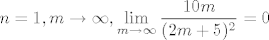 . Dakle infimum od S ne postoji. . Dakle infimum od S ne postoji.
Za supremum moramo dobiti neku gornju medu ovog izraza odnosno od cega je 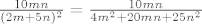 manje ili jednako. Buduci da je manje ili jednako. Buduci da je 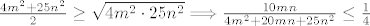 , a za , a za 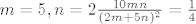 . Dakle supremum od S je . Dakle supremum od S je 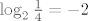
To je valjda to, ak si htio samo hint ispricavam se.
Zadnja promjena: Ivanaa; 17:43 uto, 28. 12. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Ivanaa
Forumaš(ica)
Pridružen/a: 18. 10. 2010. (22:26:06)
Postovi: (35)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:20 uto, 28. 12. 2010 Naslov: Postano: 17:20 uto, 28. 12. 2010 Naslov: |
    |
|
|
[quote="Joker"]http://web.math.hr/nastava/analiza/kol/ma1-0708-kol2.pdf
jel bi rijesio netko 3. zadatak iz prve grupe,a za drugu samo ideja da vidim dal mi je tocno...
u prvoj grupi nemogu nikako rastaviti ovaj skup na nesto normalno =SS[/quote]
Rasprava vezana za ovaj iz prve grupe se već otegnula [url=http://degiorgi.math.hr/forum/viewtopic.php?t=15989&postdays=0&postorder=asc&&start=0]ovdje[/url] pri kraju, i nastavlja se na sljedećoj stranici.
Standardna fora za nešto tog tipa kao u drugoj grupi je supstitucija [latex]q = \frac{m}{n}[/latex], pa onda gledati na to kao funkciju realne varijable. Za takve izraze se kaže da su homogeni, jer su stupnjevi svih "monoma" jednaki.
U jednom trenutku se ipak treba iskoristiti i A-G nejednakost, kad već ne smijete derivirati.
EDIT: Link koji sam dao se odnosi na zadatak iz zadaće koji se razlikuje od onoga iz kolokvija u jednom predznaku. Ipak, ideje/frustracije su iste. :)
EDIT2: Ispada da se kolokvijski zadatak ne može riješiti elegantno kao onaj iz zadaće, pa bolje da stavim direktni link na mornikov [url=http://degiorgi.math.hr/forum/viewtopic.php?t=14212]post[/url].
| Joker (napisa): | http://web.math.hr/nastava/analiza/kol/ma1-0708-kol2.pdf
jel bi rijesio netko 3. zadatak iz prve grupe,a za drugu samo ideja da vidim dal mi je tocno...
u prvoj grupi nemogu nikako rastaviti ovaj skup na nesto normalno =SS |
Rasprava vezana za ovaj iz prve grupe se već otegnula ovdje pri kraju, i nastavlja se na sljedećoj stranici.
Standardna fora za nešto tog tipa kao u drugoj grupi je supstitucija  , pa onda gledati na to kao funkciju realne varijable. Za takve izraze se kaže da su homogeni, jer su stupnjevi svih "monoma" jednaki. , pa onda gledati na to kao funkciju realne varijable. Za takve izraze se kaže da su homogeni, jer su stupnjevi svih "monoma" jednaki.
U jednom trenutku se ipak treba iskoristiti i A-G nejednakost, kad već ne smijete derivirati.
EDIT: Link koji sam dao se odnosi na zadatak iz zadaće koji se razlikuje od onoga iz kolokvija u jednom predznaku. Ipak, ideje/frustracije su iste. 
EDIT2: Ispada da se kolokvijski zadatak ne može riješiti elegantno kao onaj iz zadaće, pa bolje da stavim direktni link na mornikov post.
Zadnja promjena: pmli; 18:40 uto, 28. 12. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:11 uto, 28. 12. 2010 Naslov: Postano: 18:11 uto, 28. 12. 2010 Naslov: |
    |
|
|
Smijem li samo pripomenuti da ovo što imaš u drugom linku nije isto početnom zadatku: tebi treba [latex]\displaystyle\frac{1}{x^2+2x+5}[/latex], a ne [latex]x^2+.5x+.2x[/latex]. Ne znam jesi li se tu nešto zeznula s WolframAlphom ili nešto, ali te dvije stvari očito nisu iste (čak i ako objasnimo nestajanje ovog razlomka time da je supremum razlomka u ovom slučaju recipročan infimumu brojnika i obratno).
A ideja je sve u svemu dobra, samo što izvlačiš krive zaključke: skup [latex]T:=\{x^2+2x+5: x\in\mathbb{Q}^+\}[/latex] uistinu nije omeđen odozgo. Također, svi njegovi članovi su pozitivni, što će reći i da su svi članovi skupa [latex]S:=\displaystyle\{\frac{1}{x^2+2x+5}: x\in\mathbb{Q}^+\}[/latex] pozitivni.
Dakle, [latex]\sup T=+\infty[/latex]. Stoga, možemo reći da je [latex]\inf S=0[/latex]. Možda bi tu trebalo biti nešto precizniji, ali stvar je dosta jasna: [latex]\inf S\geq 0[/latex] jer su svi članovi pozitivni, a ako za svaki [latex]M\in \mathbb{R}^+[/latex] imamo [latex]p\in T[/latex] takav da je [latex]p>M[/latex] (a upravo smo rekli da imamo), onda je [latex]q:=\displaystyle\frac{1}{p}\in S[/latex] i [latex]q<\displaystyle\frac{1}{M}[/latex].
Što se supremuma tiče, lako utvrdimo da je [latex]\inf T=5[/latex]. (Neprekidna funkcija [latex]f(x)=x^2+2x+5[/latex] je strogo rastuća na [latex]\mathbb{R}^+[/latex], pa joj je infimum "kod [latex]0[/latex]", a nuli možemo doći proizvoljno blizu s pozitivnim racionalnim brojevima). Stoga, [latex]\sup S=\displaystyle\frac{1}{5}[/latex]. Možda bi i tu trebalo kakvo pojašnjenje u stilu gore, možda ste i to spominjali kao nekakvu "gotovu" tvrdnju, ali stvar je sve u svemu dosta jasna. Ne znam koliko ste detaljno to objašnjavali, reci ako treba više.
Eto, i to bi trebalo biti to. :)
---
Aha, Jokerovo pitanje. Urgh, to s 2008. bi trebalo zabraniti. :D OK, taj iz prve grupe sam [url=http://degiorgi.math.hr/forum/viewtopic.php?p=128266#128266]ovdje[/url] kakti riješio i diskutirao eventualnu grešku u setu zadataka iz te godine, da sad ne ulazimo ponovno u to. Uglavnom, ovaj iz prve grupe je još kao rješiv, ali nekako nisam baš uvjeren da je bilo namijenjeno da se sve ovo radi. (Možda postoji i neko lakše rješenje, doduše, ne znam... :?) Pretpostavio bih da je ipak ideja bila da se stvar relativno lako može razdijeliti na "umnožaK" dva skupa - jedan koji ovisi samo o jednoj varijabli, a drugi o drugoj, ali to u tom zadatku nisam u brojniku uspio izvesti. Doduše, možda griješim.
Druga grupa, na sreću (možda/valjda i jedina), nema greške: samo podijeli sve s [latex]m^2[/latex] (ili [latex]n^2[/latex], što god te više veseli, pa dalje idi sa supstitucijom [latex]q:=\displaystyle\frac{m}{n}[/latex] (ili recipročnom), kako ste to već radili na vježbama. Reci ako će trebati kakva pomoć.
Aha, sad vidim da je pmli već odgovorio. Meh. Neka ostane, glupo mi sad brisati.
---
EDIT: Glup i ne zna pročitati zadatak. mornik, to jest. Isprike. :oops: Sad je valjda OK.
Smijem li samo pripomenuti da ovo što imaš u drugom linku nije isto početnom zadatku: tebi treba 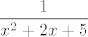 , a ne , a ne 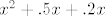 . Ne znam jesi li se tu nešto zeznula s WolframAlphom ili nešto, ali te dvije stvari očito nisu iste (čak i ako objasnimo nestajanje ovog razlomka time da je supremum razlomka u ovom slučaju recipročan infimumu brojnika i obratno). . Ne znam jesi li se tu nešto zeznula s WolframAlphom ili nešto, ali te dvije stvari očito nisu iste (čak i ako objasnimo nestajanje ovog razlomka time da je supremum razlomka u ovom slučaju recipročan infimumu brojnika i obratno).
A ideja je sve u svemu dobra, samo što izvlačiš krive zaključke: skup 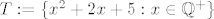 uistinu nije omeđen odozgo. Također, svi njegovi članovi su pozitivni, što će reći i da su svi članovi skupa uistinu nije omeđen odozgo. Također, svi njegovi članovi su pozitivni, što će reći i da su svi članovi skupa 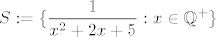 pozitivni. pozitivni.
Dakle, 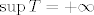 . Stoga, možemo reći da je . Stoga, možemo reći da je 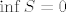 . Možda bi tu trebalo biti nešto precizniji, ali stvar je dosta jasna: . Možda bi tu trebalo biti nešto precizniji, ali stvar je dosta jasna: 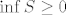 jer su svi članovi pozitivni, a ako za svaki jer su svi članovi pozitivni, a ako za svaki 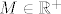 imamo imamo 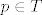 takav da je takav da je 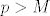 (a upravo smo rekli da imamo), onda je (a upravo smo rekli da imamo), onda je 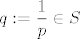 i i 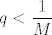 . .
Što se supremuma tiče, lako utvrdimo da je 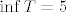 . (Neprekidna funkcija . (Neprekidna funkcija 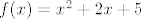 je strogo rastuća na je strogo rastuća na 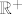 , pa joj je infimum "kod , pa joj je infimum "kod  ", a nuli možemo doći proizvoljno blizu s pozitivnim racionalnim brojevima). Stoga, ", a nuli možemo doći proizvoljno blizu s pozitivnim racionalnim brojevima). Stoga, 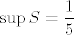 . Možda bi i tu trebalo kakvo pojašnjenje u stilu gore, možda ste i to spominjali kao nekakvu "gotovu" tvrdnju, ali stvar je sve u svemu dosta jasna. Ne znam koliko ste detaljno to objašnjavali, reci ako treba više. . Možda bi i tu trebalo kakvo pojašnjenje u stilu gore, možda ste i to spominjali kao nekakvu "gotovu" tvrdnju, ali stvar je sve u svemu dosta jasna. Ne znam koliko ste detaljno to objašnjavali, reci ako treba više.
Eto, i to bi trebalo biti to. 
—
Aha, Jokerovo pitanje. Urgh, to s 2008. bi trebalo zabraniti.  OK, taj iz prve grupe sam ovdje kakti riješio i diskutirao eventualnu grešku u setu zadataka iz te godine, da sad ne ulazimo ponovno u to. Uglavnom, ovaj iz prve grupe je još kao rješiv, ali nekako nisam baš uvjeren da je bilo namijenjeno da se sve ovo radi. (Možda postoji i neko lakše rješenje, doduše, ne znam... OK, taj iz prve grupe sam ovdje kakti riješio i diskutirao eventualnu grešku u setu zadataka iz te godine, da sad ne ulazimo ponovno u to. Uglavnom, ovaj iz prve grupe je još kao rješiv, ali nekako nisam baš uvjeren da je bilo namijenjeno da se sve ovo radi. (Možda postoji i neko lakše rješenje, doduše, ne znam...  ) Pretpostavio bih da je ipak ideja bila da se stvar relativno lako može razdijeliti na "umnožaK" dva skupa - jedan koji ovisi samo o jednoj varijabli, a drugi o drugoj, ali to u tom zadatku nisam u brojniku uspio izvesti. Doduše, možda griješim. ) Pretpostavio bih da je ipak ideja bila da se stvar relativno lako može razdijeliti na "umnožaK" dva skupa - jedan koji ovisi samo o jednoj varijabli, a drugi o drugoj, ali to u tom zadatku nisam u brojniku uspio izvesti. Doduše, možda griješim.
Druga grupa, na sreću (možda/valjda i jedina), nema greške: samo podijeli sve s 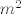 (ili (ili 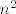 , što god te više veseli, pa dalje idi sa supstitucijom , što god te više veseli, pa dalje idi sa supstitucijom 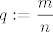 (ili recipročnom), kako ste to već radili na vježbama. Reci ako će trebati kakva pomoć. (ili recipročnom), kako ste to već radili na vježbama. Reci ako će trebati kakva pomoć.
Aha, sad vidim da je pmli već odgovorio. Meh. Neka ostane, glupo mi sad brisati.
—
EDIT: Glup i ne zna pročitati zadatak. mornik, to jest. Isprike.  Sad je valjda OK. Sad je valjda OK.
Zadnja promjena: mornik; 19:54 uto, 28. 12. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:48 uto, 28. 12. 2010 Naslov: Postano: 19:48 uto, 28. 12. 2010 Naslov: |
    |
|
|
Ne znam, možda je ovo već prekasno navečer za mene, ali nekako mi se čini da si u tom slučaju koristila [latex]\displaystyle\frac{n^2}{m^2+2mn+5n^2}=\frac{n^2}{m^2}+\frac{n^2}{2mn}+\frac{n^2}{5n^2}[/latex], što (očito) nikako ne stoji. :) Naravno, i u tom slučaju je WolframAlpha krivo protumačio što ti hoćeš (onaj [latex]x[/latex] na kraju je višak), ali nebitno. :)
Inače, sad sam vidio kod sebe grešku, krivo sam pročitao zadatak (u nazivniku je [latex]m^2+2mn+5n^2[/latex], a ja sam konstantno pisao [latex]m^2+5mn+2n^2[/latex]. Nema neke razlike (osim u završnom rezultatu), ali sad ću to izmijeniti. Sorry. :oops: Zbunile su me ove [latex].5[/latex] i [latex].2[/latex] kod tebe, mislio sam da su samo točkice viška. :D
Ne znam, možda je ovo već prekasno navečer za mene, ali nekako mi se čini da si u tom slučaju koristila 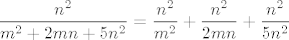 , što (očito) nikako ne stoji. , što (očito) nikako ne stoji.  Naravno, i u tom slučaju je WolframAlpha krivo protumačio što ti hoćeš (onaj Naravno, i u tom slučaju je WolframAlpha krivo protumačio što ti hoćeš (onaj  na kraju je višak), ali nebitno. na kraju je višak), ali nebitno. 
Inače, sad sam vidio kod sebe grešku, krivo sam pročitao zadatak (u nazivniku je 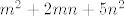 , a ja sam konstantno pisao , a ja sam konstantno pisao 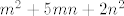 . Nema neke razlike (osim u završnom rezultatu), ali sad ću to izmijeniti. Sorry. . Nema neke razlike (osim u završnom rezultatu), ali sad ću to izmijeniti. Sorry.  Zbunile su me ove Zbunile su me ove 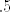 i i 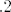 kod tebe, mislio sam da su samo točkice viška. kod tebe, mislio sam da su samo točkice viška. 
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:25 uto, 28. 12. 2010 Naslov: Postano: 21:25 uto, 28. 12. 2010 Naslov: |
    |
|
|
Nisi rekla/o o kojoj se grupi radi, pa evo samo neki hintovi i polurješenja.
U prvoj grupi, prvo izluči [latex]\displaystyle\frac{e^{\sin(x)}}{e^x}[/latex] - to ti neće stvarati probleme. Nakon toga promatraj što znaš o limesima od [latex]\displaystyle\frac{x}{e^{x}-1}[/latex], [latex]\displaystyle\frac{e^{2\sin(x)\cos(x)-\sin(x)}-1}{2\sin(x)\cos(x)-\sin(x)}[/latex] i [latex]\displaystyle\frac{2\sin(x)\cos(x)-\sin(x)}{x}[/latex]. Svi od tih limesa bi ti trebali biti poznati/lako izračunljivi. Finalni rezultat bi mogao (ali ne mora :P) biti [latex]1[/latex].
U drugoj grupi, smisleno je usporediti [latex]\sin(x)-\sinh(2x)[/latex] s [latex]x[/latex], tj. pronaći limes od [latex]\displaystyle\frac{\sin(x)-\sinh(2x)}{x}[/latex]. To nije teško. Nakon toga, usporedi [latex]\ln(1+e^x-e^{2x})[/latex] s [latex]e^x-e^{2x}[/latex], što je poznati limes. Preostaje još da odrediš limes od [latex]\displaystyle\frac{e^x-e^{2x}}{x}[/latex], što smo već napravili u prvoj grupi: izlučimo [latex]e^x[/latex] pa imamo poznati limes. Finalni rezultat bi tu trebao biti opet [latex]1[/latex].
Treča grupa se zapravo svodi na tehnike koje smo koristili u prvoj i drugoj. Prvo odredi limes od [latex]\displaystyle\frac{e^{\cos(x)-\cosh(x)}-1}{\cos(x)-\cosh(x)}[/latex], pa dolje izluči [latex]e^{x^2}[/latex], s čim nećeš imati problema. Dalje, znaš i limes od [latex]\displaystyle{x^2}{1-e^{x^2}}[/latex]. Naposljetku preostaje da odredimo limes od [latex]\displaystyle\frac{\cos(x)-\cosh(x)}{x^2}[/latex], a to znaš: [latex]\displaystyle\frac{\cos(x)-\cosh(x)}{x^2}=\frac{(\cos(x)-1)-(\cosh(x)-1)}{x^2}[/latex]. Kad sve to izmnožimo (s tim da ne smijemo limese "parcijalno" računati, pa ići s njima dalje u račun, nego ih sve moramo izračunati na kraju!), dobivamo završni limes koji bi i po treći put trebao iznositi [latex]1[/latex].
Naposljetku, četvrta grupa je uvijek ista. Prvo, hajde da izlučimo [latex]e^{2x^2}[/latex] u brojniku (vjerojatno može i [latex]e^{\sin^2(x)}[/latex]). Sad gore znamo limes od [latex]\displaystyle\frac{e^{\sin^2(x)-2x^2}-1}{\sin^2(x)-2x^2}[/latex]. S druge strane, dolje znamo limes od [latex]\displaystyle\frac{\cos(x)-1}{2\ln(\cos(x))}[/latex] (primijeti da je [latex]\cos(x)=1+(\cos(x)-1)[/latex]). Naposljetku valja izračunati limes od [latex]\displaystyle\frac{\sin^2(x)-2x^2}{\cos(x)-1}[/latex], a to znamo: podijeli i brojnik i nazivnik s [latex]x^2[/latex]. I ovaj bi put, ako se ne varam, limes mogao biti [latex]1[/latex].
Uh. Nisu tako kratki ovi zadaci, pogotovo za pisati u TeX-u. :P
E, sad kad sam napisao, ti promijeniš post, vidim. :D
Nisi rekla/o o kojoj se grupi radi, pa evo samo neki hintovi i polurješenja.
U prvoj grupi, prvo izluči 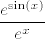 - to ti neće stvarati probleme. Nakon toga promatraj što znaš o limesima od - to ti neće stvarati probleme. Nakon toga promatraj što znaš o limesima od 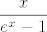 , , 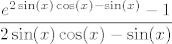 i i 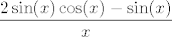 . Svi od tih limesa bi ti trebali biti poznati/lako izračunljivi. Finalni rezultat bi mogao (ali ne mora . Svi od tih limesa bi ti trebali biti poznati/lako izračunljivi. Finalni rezultat bi mogao (ali ne mora  ) biti ) biti  . .
U drugoj grupi, smisleno je usporediti 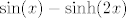 s s  , tj. pronaći limes od , tj. pronaći limes od 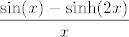 . To nije teško. Nakon toga, usporedi . To nije teško. Nakon toga, usporedi 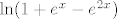 s s 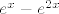 , što je poznati limes. Preostaje još da odrediš limes od , što je poznati limes. Preostaje još da odrediš limes od 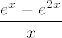 , što smo već napravili u prvoj grupi: izlučimo , što smo već napravili u prvoj grupi: izlučimo 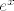 pa imamo poznati limes. Finalni rezultat bi tu trebao biti opet pa imamo poznati limes. Finalni rezultat bi tu trebao biti opet  . .
Treča grupa se zapravo svodi na tehnike koje smo koristili u prvoj i drugoj. Prvo odredi limes od 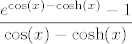 , pa dolje izluči , pa dolje izluči 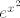 , s čim nećeš imati problema. Dalje, znaš i limes od , s čim nećeš imati problema. Dalje, znaš i limes od  . Naposljetku preostaje da odredimo limes od . Naposljetku preostaje da odredimo limes od 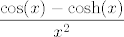 , a to znaš: , a to znaš: 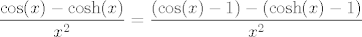 . Kad sve to izmnožimo (s tim da ne smijemo limese "parcijalno" računati, pa ići s njima dalje u račun, nego ih sve moramo izračunati na kraju!), dobivamo završni limes koji bi i po treći put trebao iznositi . Kad sve to izmnožimo (s tim da ne smijemo limese "parcijalno" računati, pa ići s njima dalje u račun, nego ih sve moramo izračunati na kraju!), dobivamo završni limes koji bi i po treći put trebao iznositi  . .
Naposljetku, četvrta grupa je uvijek ista. Prvo, hajde da izlučimo 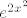 u brojniku (vjerojatno može i u brojniku (vjerojatno može i 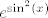 ). Sad gore znamo limes od ). Sad gore znamo limes od 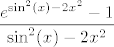 . S druge strane, dolje znamo limes od . S druge strane, dolje znamo limes od 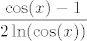 (primijeti da je (primijeti da je 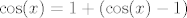 ). Naposljetku valja izračunati limes od ). Naposljetku valja izračunati limes od 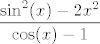 , a to znamo: podijeli i brojnik i nazivnik s , a to znamo: podijeli i brojnik i nazivnik s 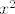 . I ovaj bi put, ako se ne varam, limes mogao biti . I ovaj bi put, ako se ne varam, limes mogao biti  . .
Uh. Nisu tako kratki ovi zadaci, pogotovo za pisati u TeX-u. 
E, sad kad sam napisao, ti promijeniš post, vidim. 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
 Postano: 21:26 uto, 28. 12. 2010 Naslov: Postano: 21:26 uto, 28. 12. 2010 Naslov: |
    |
|
|
Druga grupa, na sreću (možda/valjda i jedina), nema greške: samo podijeli sve s [latex]m^2[/latex] (ili [latex]n^2[/latex], što god te više veseli, pa dalje idi sa supstitucijom [latex]q:=\displaystyle\frac{m}{n}[/latex] (ili recipročnom), kako ste to već radili na vježbama. Reci ako će trebati kakva pomoć.
Ej, evo to sam i radila prije nego sam postavila pitanje,dakle dobijem skup
S={ q / (q^2 + 3q + 4) }
supremum mi ispada 1/7, a infimum 0...i nisam sigurna da je to dobro..=) pa?? =))
Druga grupa, na sreću (možda/valjda i jedina), nema greške: samo podijeli sve s 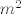 (ili (ili 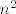 , što god te više veseli, pa dalje idi sa supstitucijom , što god te više veseli, pa dalje idi sa supstitucijom 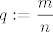 (ili recipročnom), kako ste to već radili na vježbama. Reci ako će trebati kakva pomoć. (ili recipročnom), kako ste to već radili na vježbama. Reci ako će trebati kakva pomoć.
Ej, evo to sam i radila prije nego sam postavila pitanje,dakle dobijem skup
S={ q / (q^2 + 3q + 4) }
supremum mi ispada 1/7, a infimum 0...i nisam sigurna da je to dobro..=) pa?? =))
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
 Postano: 23:44 uto, 28. 12. 2010 Naslov: Postano: 23:44 uto, 28. 12. 2010 Naslov: |
    |
|
|
[quote="mornik"]Ne znam, možda je ovo već prekasno navečer za mene, ali nekako mi se čini da si u tom slučaju koristila [latex]\displaystyle\frac{n^2}{m^2+2mn+5n^2}=\frac{n^2}{m^2}+\frac{n^2}{2mn}+\frac{n^2}{5n^2}[/latex], što (očito) nikako ne stoji. :)
[/quote]
Zasto ne stoji, zar nije svejedno je li n ili m u brojniku? I ako nije, zasto nije?
| mornik (napisa): | Ne znam, možda je ovo već prekasno navečer za mene, ali nekako mi se čini da si u tom slučaju koristila 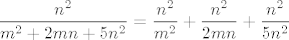 , što (očito) nikako ne stoji. , što (očito) nikako ne stoji. 
|
Zasto ne stoji, zar nije svejedno je li n ili m u brojniku? I ako nije, zasto nije?
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 0:17 sri, 29. 12. 2010 Naslov: Postano: 0:17 sri, 29. 12. 2010 Naslov: |
    |
|
|
[quote="A-tom"][quote="mornik"]Ne znam, možda je ovo već prekasno navečer za mene, ali nekako mi se čini da si u tom slučaju koristila [latex]\displaystyle\frac{n^2}{m^2+2mn+5n^2}=\frac{n^2}{m^2}+\frac{n^2}{2mn}+\frac{n^2}{5n^2}[/latex], što (očito) nikako ne stoji. :)
[/quote]
Zasto ne stoji, zar nije svejedno je li n ili m u brojniku? I ako nije, zasto nije?[/quote]
Evo malog kontraprimjera, kad bi ovo što je mornik napisao da ne vrijedi vrijedilo, onda bi bilo:
0.25=1/(2+2) =1/2 +1/2 =1 :lol:
| A-tom (napisa): | | mornik (napisa): | Ne znam, možda je ovo već prekasno navečer za mene, ali nekako mi se čini da si u tom slučaju koristila 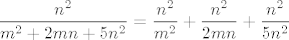 , što (očito) nikako ne stoji. , što (očito) nikako ne stoji. 
|
Zasto ne stoji, zar nije svejedno je li n ili m u brojniku? I ako nije, zasto nije? |
Evo malog kontraprimjera, kad bi ovo što je mornik napisao da ne vrijedi vrijedilo, onda bi bilo:
0.25=1/(2+2) =1/2 +1/2 =1 
|
|
| [Vrh] |
|
rom
Forumaš(ica)
Pridružen/a: 26. 10. 2010. (11:10:35)
Postovi: (2D)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 13:29 sri, 29. 12. 2010 Naslov: Postano: 13:29 sri, 29. 12. 2010 Naslov: |
    |
|
|
Pa da, za konvergenciju je dovoljno da je niz ogranicen i monoton od nekog n nadalje. Za rjesavanje zadataka, to znaci da moras dobro odabrati bazu indukcije...
Obicno iz uvjeta [latex]a_{n+1}>a_n[/latex] prilicno brzo izadje kakav n mora biti...
Inace, ovaj niz iz kolokvija (npr, prva grupa) izgleda ovako:
0 0 1/3 1/3 7/18...
(tj raste cijelo vrijeme)
Ako stavimo [latex]a_{n+2}>a_{n+1}[/latex], dobivamo [latex]\frac{1}{2}(a_{n+1}a_n-a_na_{n-1})[/latex]
iz toga vidimo da je dovoljno da imamo [latex]a_{n+1}>a_n>a_{n-1}[/latex] da bi bilo [latex]a_{n+2}>a_{n+1}[/latex], a taj uvjet imamo zadovoljen vec od prva 3 clana, dakle niz je od pocetka rastuci
Pa da, za konvergenciju je dovoljno da je niz ogranicen i monoton od nekog n nadalje. Za rjesavanje zadataka, to znaci da moras dobro odabrati bazu indukcije...
Obicno iz uvjeta 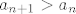 prilicno brzo izadje kakav n mora biti... prilicno brzo izadje kakav n mora biti...
Inace, ovaj niz iz kolokvija (npr, prva grupa) izgleda ovako:
0 0 1/3 1/3 7/18...
(tj raste cijelo vrijeme)
Ako stavimo 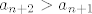 , dobivamo , dobivamo 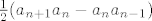
iz toga vidimo da je dovoljno da imamo 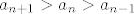 da bi bilo da bi bilo 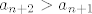 , a taj uvjet imamo zadovoljen vec od prva 3 clana, dakle niz je od pocetka rastuci , a taj uvjet imamo zadovoljen vec od prva 3 clana, dakle niz je od pocetka rastuci
Zadnja promjena: pbakic; 14:11 sri, 29. 12. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
|















