| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 23:00 sri, 5. 1. 2011 Naslov: Postano: 23:00 sri, 5. 1. 2011 Naslov: |
    |
|
|
Moze netko nakratko, odnosno jednostavno samo objasniti, kad u zadatku kazu odredite limes, sup, inf [b]AKO POSTOJE [/b],
sta treba pri limesu vrijediti (da je niz ogranicen i monoton da bi postojao limes?? ili... ), a sta pri sup i inf ....
kao znam, ali mi se sve sad nesto pobrkalo ... :S :S :S
Moze netko nakratko, odnosno jednostavno samo objasniti, kad u zadatku kazu odredite limes, sup, inf AKO POSTOJE ,
sta treba pri limesu vrijediti (da je niz ogranicen i monoton da bi postojao limes?? ili... ), a sta pri sup i inf ....
kao znam, ali mi se sve sad nesto pobrkalo ... :S :S :S
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 0:46 čet, 6. 1. 2011 Naslov: Postano: 0:46 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote="pupi"][quote="frutabella"]6. zad:
d) 1[/quote]
Na vježbama smo dobili rezultat 0 (koristeći teorem o sendviču).[/quote]
Jeste, jeste, u pravu si, mah blentavu gresku uradih.
Ako si rjesila do 10, imam rjesenja i od toga pa mozemo provjeriti, ma da mi 7 nije jasan... :S
:D
| pupi (napisa): | | frutabella (napisa): | 6. zad:
d) 1 |
Na vježbama smo dobili rezultat 0 (koristeći teorem o sendviču). |
Jeste, jeste, u pravu si, mah blentavu gresku uradih.
Ako si rjesila do 10, imam rjesenja i od toga pa mozemo provjeriti, ma da mi 7 nije jasan... :S

|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 8:26 čet, 6. 1. 2011 Naslov: Postano: 8:26 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote="frutabella"]Moze netko nakratko, odnosno jednostavno samo objasniti, kad u zadatku kazu odredite limes, sup, inf [b]AKO POSTOJE [/b],
sta treba pri limesu vrijediti (da je niz ogranicen i monoton da bi postojao limes?? ili... ), a sta pri sup i inf ....
kao znam, ali mi se sve sad nesto pobrkalo ... :S :S :S[/quote]
Nije nužno da je niz ograničen i monoton da bi postojao limes. Zapravo, dobro, nužno je da je ograničen (to ste dokazivali), ali to i nije dovoljno: niz [latex](-1)^n[/latex] je ograničen, ali nije konvergentan. Monotonost nije ni nužna ni dovoljna: npr. pogledaj niz [latex]\displaystyle\frac{(-1)^n}{n}[/latex] - on je ograničen, ali nije monoton, a limes svejedno postoji. Sve u svemu, ne postoji neka baš jednostavna ekvivalencija postojanju limesa, postoje neki dovoljni uvjeti (stalno radite s tom implikacijom "monotonost i ograničenost [latex]\Rightarrow[/latex] konvergencija"), a ako sve zapne, vjerojatno moraš početi gledati po definiciji. :)
Što se tiče postojanja supremuma i infimuma (u [latex]\mathbb{R}[/latex], vidi [url=http://degiorgi.math.hr/forum/viewtopic.php?p=147862#147862]tu[/url] za začkoljice s ostalim skupovima), nužno je i dovoljno (to ti garantira aksiom A15) da niz/skup bude ograničen odozgo (za supremum) i odozdo (za infimum). Stoga, tu je situacija puno lakša nego kod limesa.
| frutabella (napisa): | Moze netko nakratko, odnosno jednostavno samo objasniti, kad u zadatku kazu odredite limes, sup, inf AKO POSTOJE ,
sta treba pri limesu vrijediti (da je niz ogranicen i monoton da bi postojao limes?? ili... ), a sta pri sup i inf ....
kao znam, ali mi se sve sad nesto pobrkalo ... :S :S :S |
Nije nužno da je niz ograničen i monoton da bi postojao limes. Zapravo, dobro, nužno je da je ograničen (to ste dokazivali), ali to i nije dovoljno: niz 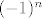 je ograničen, ali nije konvergentan. Monotonost nije ni nužna ni dovoljna: npr. pogledaj niz je ograničen, ali nije konvergentan. Monotonost nije ni nužna ni dovoljna: npr. pogledaj niz 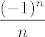 - on je ograničen, ali nije monoton, a limes svejedno postoji. Sve u svemu, ne postoji neka baš jednostavna ekvivalencija postojanju limesa, postoje neki dovoljni uvjeti (stalno radite s tom implikacijom "monotonost i ograničenost - on je ograničen, ali nije monoton, a limes svejedno postoji. Sve u svemu, ne postoji neka baš jednostavna ekvivalencija postojanju limesa, postoje neki dovoljni uvjeti (stalno radite s tom implikacijom "monotonost i ograničenost  konvergencija"), a ako sve zapne, vjerojatno moraš početi gledati po definiciji. konvergencija"), a ako sve zapne, vjerojatno moraš početi gledati po definiciji. 
Što se tiče postojanja supremuma i infimuma (u  , vidi tu za začkoljice s ostalim skupovima), nužno je i dovoljno (to ti garantira aksiom A15) da niz/skup bude ograničen odozgo (za supremum) i odozdo (za infimum). Stoga, tu je situacija puno lakša nego kod limesa. , vidi tu za začkoljice s ostalim skupovima), nužno je i dovoljno (to ti garantira aksiom A15) da niz/skup bude ograničen odozgo (za supremum) i odozdo (za infimum). Stoga, tu je situacija puno lakša nego kod limesa.
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
|














