| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:59 uto, 30. 8. 2005 Naslov: Postano: 23:59 uto, 30. 8. 2005 Naslov: |
    |
|
|
[quote="vsego"]Valjda mislis na Integral od sqrt(t)dt? 8) A to je obicna potencija (t^(1/2)) sto se lako integrira. :)[/quote]
Ne, ne mislim na to. 8)
[quote]Ali ti nemas tgx*1/cosx*dx nego sqrt(tgx*1/cosx)dx... :-s[/quote]
da, zato i pitam da li se može iskoristiti kao substitucija, jer taj dx izvan korijena predstavlja problem, ali očito ne može. :)
no bez obzira na ovaj zadatak, da li postoji integral od sqrt(dx) ?
i drugo pitanje, da li se prijespomenuti dx može ugurati pod korijen (općenito) i da li onda poprima vrijednost (dx)^2 ?
| vsego (napisa): | Valjda mislis na Integral od sqrt(t)dt?  A to je obicna potencija (t^(1/2)) sto se lako integrira. A to je obicna potencija (t^(1/2)) sto se lako integrira.  |
Ne, ne mislim na to. 
| Citat: | Ali ti nemas tgx*1/cosx*dx nego sqrt(tgx*1/cosx)dx...  |
da, zato i pitam da li se može iskoristiti kao substitucija, jer taj dx izvan korijena predstavlja problem, ali očito ne može. 
no bez obzira na ovaj zadatak, da li postoji integral od sqrt(dx) ?
i drugo pitanje, da li se prijespomenuti dx može ugurati pod korijen (općenito) i da li onda poprima vrijednost (dx)^2 ?
_________________
The Dude Abides
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 0:14 sri, 31. 8. 2005 Naslov: Postano: 0:14 sri, 31. 8. 2005 Naslov: |
    |
|
|
:blueshock: Ne mozes to raditi s dx. :blueshock: Prouci odakle taj dx dolazi (Darbouxove sume i sl), pa ce biti jasno zasto ne mozes... 8)
Inace, Mathematica kaze:
[latex]\int {\sqrt{\sin x} \over \cos{x}} dx = \frac{2 \,
_2F_1\left(\frac{1}{4},\frac{1}{4};\frac{5}{4};\sec
^2(x)\right) \sqrt[4]{-\tan ^2(x)}}{\sin
^{\frac{1}{2}}(x)} \\
= \frac{B_{\sec ^2(x)}\left(\frac{1}{4},\frac{3}{4}\right)
\sqrt[4]{-\tan ^2(x)}}{2 \sqrt[4]{\sec ^2(x)} \sin
^{\frac{1}{2}}(x)}[/latex]
Cini mi se da ne postoji "lijepo" rjesenje tvog integrala. :(
 Ne mozes to raditi s dx. Ne mozes to raditi s dx.  Prouci odakle taj dx dolazi (Darbouxove sume i sl), pa ce biti jasno zasto ne mozes... Prouci odakle taj dx dolazi (Darbouxove sume i sl), pa ce biti jasno zasto ne mozes... 
Inace, Mathematica kaze:
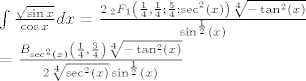
Cini mi se da ne postoji "lijepo" rjesenje tvog integrala. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
|











