| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
 Postano: 15:12 sri, 8. 2. 2006 Naslov: Re: Limes - Pitanje Postano: 15:12 sri, 8. 2. 2006 Naslov: Re: Limes - Pitanje |
    |
|
|
[quote="Tiho"]Limes kad x --> 0 (1+tgx)^1/sinx
Molio bih da mi netko HITNO riješi ovaj limes... hvala unaprijed..[/quote]
ajme, kad je tako hitno, evo jurim se... samo malo :drinking: ahhh.. ajmo 3,4 sad:
dakle dani limes je oblika [latex]1^{\infty}[/latex], pa je
[latex]\lim_{x \rightarrow 0} (1+\mathop{\mathrm{tg}}x)^{\frac{1}{\sin x}}=e^{\lim_{x \rightarrow 0} (\mathop{1+\mathrm{tg}}x -1)\cdot{\frac{1}{\sin x}}}=[/latex][latex]e^{\lim_{x \rightarrow 0} \mathop{\mathrm{tg}}x\cdot{\frac{1}{\sin x}}}=e^{\lim_{x \rightarrow 0}\frac{1}{\cos x}}=e[/latex].
evo ga, stigo sam, aj bok i sretno.
dr. Exodus :croatia:
| Tiho (napisa): | Limes kad x → 0 (1+tgx)^1/sinx
Molio bih da mi netko HITNO riješi ovaj limes... hvala unaprijed.. |
ajme, kad je tako hitno, evo jurim se... samo malo  ahhh.. ajmo 3,4 sad: ahhh.. ajmo 3,4 sad:
dakle dani limes je oblika 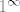 , pa je , pa je
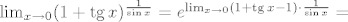 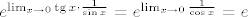 . .
evo ga, stigo sam, aj bok i sretno.
dr. Exodus 
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
vkojic
Forumaš(ica)

Pridružen/a: 01. 02. 2006. (22:44:48)
Postovi: (14)16
|
 Postano: 16:57 sri, 8. 2. 2006 Naslov: Postano: 16:57 sri, 8. 2. 2006 Naslov: |
    |
|
|
Hm, nije napisano kuda x teži, no pretpostavit cu u pi/2. Ako je tako, onda je dani limes jednak e. Naime, racuna se limes exp( lim(x-->pi/2) ctgx/cosx) = exp( lim(x-->pi/2) 1/sinx)= exp( 1/sin(pi/2) )= exp(1)=e, gdje je exp notacija za e_na_(argument) (valjda je jasno :) ) Druga je stvar ako x tezi npr. u 0, tocnije x-->0+ (tj zdesna). Onda bi dani limes bio oblika (+beskonacno)_na_1 sto je +beskonacno.
Nadam se da nisam nesto zbrljao...
Pozdrav
Hm, nije napisano kuda x teži, no pretpostavit cu u pi/2. Ako je tako, onda je dani limes jednak e. Naime, racuna se limes exp( lim(x-->pi/2) ctgx/cosx) = exp( lim(x-->pi/2) 1/sinx)= exp( 1/sin(pi/2) )= exp(1)=e, gdje je exp notacija za e_na_(argument) (valjda je jasno  ) Druga je stvar ako x tezi npr. u 0, tocnije x-->0+ (tj zdesna). Onda bi dani limes bio oblika (+beskonacno)_na_1 sto je +beskonacno. ) Druga je stvar ako x tezi npr. u 0, tocnije x-->0+ (tj zdesna). Onda bi dani limes bio oblika (+beskonacno)_na_1 sto je +beskonacno.
Nadam se da nisam nesto zbrljao...
Pozdrav
|
|
| [Vrh] |
|
Mishika
Forumaš(ica)

Pridružen/a: 28. 09. 2005. (11:32:36)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Mishika
Forumaš(ica)

Pridružen/a: 28. 09. 2005. (11:32:36)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
|












