| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
aenima
Forumaš(ica)

Pridružen/a: 17. 09. 2004. (17:03:42)
Postovi: (57)16
Spol: 
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
 Postano: 21:29 sri, 22. 11. 2006 Naslov: Re: zadačić Postano: 21:29 sri, 22. 11. 2006 Naslov: Re: zadačić |
    |
|
|
[quote="aenima"]Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ?[/quote]
Ja bih to ovako. Gledala bih A_i...skup svih nacina da na i-tom katu nitko ne izlazi!
Dakle, sto smo dobili time? [latex]|S|=n^m\,,|A_i|=(n-1)^m\,,|A_i \cap A_j|=(n-2)^m[/latex],..., [latex]|A_1 \cap A_2 \ldots \cap A_n|=(n-n)^m=0[/latex]
Upotrijebis FUI na kraju i to je to. Ja sam kao rezultat dobila da je to jednako
[latex]\sum_{k=0}^{n}{{(-1)^k} {n \choose k} (n-k)^m}[/latex]
| aenima (napisa): | | Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ? |
Ja bih to ovako. Gledala bih A_i...skup svih nacina da na i-tom katu nitko ne izlazi!
Dakle, sto smo dobili time? 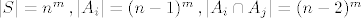 ,..., ,..., 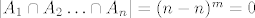
Upotrijebis FUI na kraju i to je to. Ja sam kao rezultat dobila da je to jednako
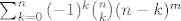
|
|
| [Vrh] |
|
aenima
Forumaš(ica)

Pridružen/a: 17. 09. 2004. (17:03:42)
Postovi: (57)16
Spol: 
|
|
| [Vrh] |
|
saskvač
Forumaš(ica)


Pridružen/a: 06. 12. 2006. (22:05:44)
Postovi: (6)16
Lokacija: Odjel za matematiku, OS
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 23:20 sri, 6. 12. 2006 Naslov: Postano: 23:20 sri, 6. 12. 2006 Naslov: |
    |
|
|
[quote="Mr.Doe"]evo jos jedan zadacic (sa roka);
koliko ima funkcija [latex]f:\mathbf{N}_n \rightarrow \mathbf{N}_n[/latex] koje su same sebi inverz i nemaju fiksnih tocaka.[/quote]
a paa.... ak nema fiksnih tocaka, onda nema fiksnih tocaka, a ak je sama sebi inverz- to bi znacilo valjda da se dva elementa zamjene mjesta. i sad, posto nema fiksnih tocaka, n bi trebao bit paran?
i onda samo brojis nacine kak odabires po 2, jer kad ih odaberes znas kamo idu - jedan u drugi
dakle, (n povrh 2)*(n-2 povrh 2)*(n-4 povrh 2)*...*(4 povrh 2)*(2 povrh 2)
ja bi htjela titulu kraljice anti-latexa :kraljica:
sta ce nam to, kaj ne vidite kak se fino da i ovak zapisat :lol:
jel tak, alen? :peglam:
| Mr.Doe (napisa): | evo jos jedan zadacic (sa roka);
koliko ima funkcija 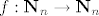 koje su same sebi inverz i nemaju fiksnih tocaka. koje su same sebi inverz i nemaju fiksnih tocaka. |
a paa.... ak nema fiksnih tocaka, onda nema fiksnih tocaka, a ak je sama sebi inverz- to bi znacilo valjda da se dva elementa zamjene mjesta. i sad, posto nema fiksnih tocaka, n bi trebao bit paran?
i onda samo brojis nacine kak odabires po 2, jer kad ih odaberes znas kamo idu - jedan u drugi
dakle, (n povrh 2)*(n-2 povrh 2)*(n-4 povrh 2)*...*(4 povrh 2)*(2 povrh 2)
ja bi htjela titulu kraljice anti-latexa 
sta ce nam to, kaj ne vidite kak se fino da i ovak zapisat 
jel tak, alen? 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
saskvač
Forumaš(ica)


Pridružen/a: 06. 12. 2006. (22:05:44)
Postovi: (6)16
Lokacija: Odjel za matematiku, OS
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 0:21 čet, 7. 12. 2006 Naslov: Re: zadačić Postano: 0:21 čet, 7. 12. 2006 Naslov: Re: zadačić |
    |
|
|
[quote="saskvač"][quote="aenima"]Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ?[/quote]
ja bi to ovako:
imamo f-ju f: [m]->[n], s tim da je br. elemenata od [m]< br.elem. [n]
dakle f-ja nije injekcija
ukupni broj f-ja [m]->[n] je n^m, a ukupni injekcija n^_m (m podvuceno)
onda je broj nacina = br. f-ja - br. injekcija
bar tako mislim
jel valja tako? :pun nade:[/quote]
cuj saskvač, meni si jako drag pa mi je zato zao sto ti ovo moram rec. mislim da je tvoje rjesenje opako krivo. ali ne brini, ja sam uvijek u zaostatku sa zadacama iz kompaktnih, sve ti u zivotu dodje na svoje. :kipslobode:
jako si dobro i bistro zakljucio da te funkcije ne mogu biti injekcije, medjutim, to ti ne jamci da su surjekcije, a presudno nam je tak nesto.
jer npr injekcija nije kad svi izadju na 1. katu jer su debeli i dalje idu pjeske, znaci to je jedna neinjekcija, no nije surjekcija i ocito nije funkcija koju mi trazimo. tak da ti oduzimas dobre funkcije, al to nisu sve! :ptice:
drzim ti fige -> :figa2:
| saskvač (napisa): | | aenima (napisa): | | Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ? |
ja bi to ovako:
imamo f-ju f: [m]→[n], s tim da je br. elemenata od [m]< br.elem. [n]
dakle f-ja nije injekcija
ukupni broj f-ja [m]→[n] je n^m, a ukupni injekcija n^_m (m podvuceno)
onda je broj nacina = br. f-ja - br. injekcija
bar tako mislim
jel valja tako? :pun nade: |
cuj saskvač, meni si jako drag pa mi je zato zao sto ti ovo moram rec. mislim da je tvoje rjesenje opako krivo. ali ne brini, ja sam uvijek u zaostatku sa zadacama iz kompaktnih, sve ti u zivotu dodje na svoje. 
jako si dobro i bistro zakljucio da te funkcije ne mogu biti injekcije, medjutim, to ti ne jamci da su surjekcije, a presudno nam je tak nesto.
jer npr injekcija nije kad svi izadju na 1. katu jer su debeli i dalje idu pjeske, znaci to je jedna neinjekcija, no nije surjekcija i ocito nije funkcija koju mi trazimo. tak da ti oduzimas dobre funkcije, al to nisu sve! 
drzim ti fige → 
|
|
| [Vrh] |
|
D4rk0
Forumaš(ica)


Pridružen/a: 08. 07. 2005. (11:06:37)
Postovi: (170)16
Spol: 
Lokacija: Nitko ne zna... Ziher mi je dobro di god da jesam ;)
|
 Postano: 1:04 čet, 7. 12. 2006 Naslov: Re: zadačić Postano: 1:04 čet, 7. 12. 2006 Naslov: Re: zadačić |
    |
|
|
[quote="hermione"][quote="aenima"]Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ?[/quote]
Ja bih to ovako. Gledala bih A_i...skup svih nacina da na i-tom katu nitko ne izlazi!
Dakle, sto smo dobili time? [latex]|S|=n^m\,,|A_i|=(n-1)^m\,,|A_i \cap A_j|=(n-2)^m[/latex],..., [latex]|A_1 \cap A_2 \ldots \cap A_n|=(n-n)^m=0[/latex]
Upotrijebis FUI na kraju i to je to. Ja sam kao rezultat dobila da je to jednako
[latex]\sum_{k=0}^{n}{{(-1)^k} {n \choose k} (n-k)^m}[/latex][/quote]
ja brijem da bi ja samo skužio da je to broj surjekcija i napisao isti tvoj rezultat :)
EDIT: spor sam... i nisam sve pročitao... vidim da je već netko prije mene bio i pravio se pametan :) ah :P
| hermione (napisa): | | aenima (napisa): | | Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ? |
Ja bih to ovako. Gledala bih A_i...skup svih nacina da na i-tom katu nitko ne izlazi!
Dakle, sto smo dobili time? 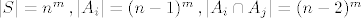 ,..., ,..., 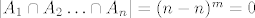
Upotrijebis FUI na kraju i to je to. Ja sam kao rezultat dobila da je to jednako
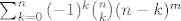 |
ja brijem da bi ja samo skužio da je to broj surjekcija i napisao isti tvoj rezultat 
EDIT: spor sam... i nisam sve pročitao... vidim da je već netko prije mene bio i pravio se pametan  ah ah 
_________________ www.spreha.net
Ljudski je griješiti, ali osjećaj je božanski... |
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
vini
Forumaš(ica)


Pridružen/a: 01. 09. 2006. (18:10:50)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 20:35 čet, 7. 12. 2006 Naslov: Postano: 20:35 čet, 7. 12. 2006 Naslov: |
    |
|
|
[quote="Ignavia"][quote="Mr.Doe"]evo jos jedan zadacic (sa roka);
koliko ima funkcija [latex]f:\mathbf{N}_n \rightarrow \mathbf{N}_n[/latex] koje su same sebi inverz i nemaju fiksnih tocaka.[/quote]
a paa.... ak nema fiksnih tocaka, onda nema fiksnih tocaka, a ak je sama sebi inverz- to bi znacilo valjda da se dva elementa zamjene mjesta. i sad, posto nema fiksnih tocaka, n bi trebao bit paran?
i onda samo brojis nacine kak odabires po 2, jer kad ih odaberes znas kamo idu - jedan u drugi
dakle, (n povrh 2)*(n-2 povrh 2)*(n-4 povrh 2)*...*(4 povrh 2)*(2 povrh 2)
ja bi htjela titulu kraljice anti-latexa :kraljica:
sta ce nam to, kaj ne vidite kak se fino da i ovak zapisat :lol:
jel tak, alen? :peglam:[/quote]
By da way, poredak biranja poskupova nije bitan pa moras podijeliti sa [latex](n/2)![/latex].
Uostalom rok je prosao :lol: .
(latex rulez!)
| Ignavia (napisa): | | Mr.Doe (napisa): | evo jos jedan zadacic (sa roka);
koliko ima funkcija 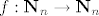 koje su same sebi inverz i nemaju fiksnih tocaka. koje su same sebi inverz i nemaju fiksnih tocaka. |
a paa.... ak nema fiksnih tocaka, onda nema fiksnih tocaka, a ak je sama sebi inverz- to bi znacilo valjda da se dva elementa zamjene mjesta. i sad, posto nema fiksnih tocaka, n bi trebao bit paran?
i onda samo brojis nacine kak odabires po 2, jer kad ih odaberes znas kamo idu - jedan u drugi
dakle, (n povrh 2)*(n-2 povrh 2)*(n-4 povrh 2)*...*(4 povrh 2)*(2 povrh 2)
ja bi htjela titulu kraljice anti-latexa 
sta ce nam to, kaj ne vidite kak se fino da i ovak zapisat 
jel tak, alen?  |
By da way, poredak biranja poskupova nije bitan pa moras podijeliti sa 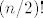 . .
Uostalom rok je prosao  . .
(latex rulez!)
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 17:29 sub, 6. 1. 2007 Naslov: Re: zadačić Postano: 17:29 sub, 6. 1. 2007 Naslov: Re: zadačić |
    |
|
|
[quote="hermione"][quote="aenima"]Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ?[/quote]
Ja bih to ovako. Gledala bih A_i...skup svih nacina da na i-tom katu nitko ne izlazi!
Dakle, sto smo dobili time? [latex]|S|=n^m\,,|A_i|=(n-1)^m\,,|A_i \cap A_j|=(n-2)^m[/latex],..., [latex]|A_1 \cap A_2 \ldots \cap A_n|=(n-n)^m=0[/latex]
Upotrijebis FUI na kraju i to je to. Ja sam kao rezultat dobila da je to jednako
[latex]\sum_{k=0}^{n}{{(-1)^k} {n \choose k} (n-k)^m}[/latex][/quote]
i ja sam dobio isto ko i ti samo bez n povrh k...
moze mi neko objasnit zasto to treba
| hermione (napisa): | | aenima (napisa): | | Zgrada ima n katova, i m ljudi se vozi liftom. NKN može tih n ljudi izići na tih n katova tako da na svakom katu iziđe bar jedna osoba ako je ukupan broj osoba veći od ukupnog broja katova ? |
Ja bih to ovako. Gledala bih A_i...skup svih nacina da na i-tom katu nitko ne izlazi!
Dakle, sto smo dobili time? 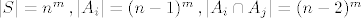 ,..., ,..., 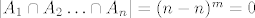
Upotrijebis FUI na kraju i to je to. Ja sam kao rezultat dobila da je to jednako
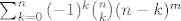 |
i ja sam dobio isto ko i ti samo bez n povrh k...
moze mi neko objasnit zasto to treba
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
|















